o(1)=(x n!a)n f(n)(a) + o((x a)n); x ! a.

Учитывая полученное равенство и (2), мы получим

локальную формулу Тейлора ( ). x 2. Разложение функции по локальной формуле Тейлора

единственно. Единственность разложения понимается в том смысле, что если f имеет n-ю производную в точке a и если

f(x) = a0 + a1(x a) + + an(x a)n + o((x a)n); x ! a; то

поэтому по теореме она разложима по локальной офрмуле Тейлора:

n

f(x) = f(a) + X k1!f(k)(a)(x a)k + o((x a)n); x ! a:

k=1

В то же время справедливо разложение f(x) = a0 + a1(x

a) + + an(x a)n + o((x a)n); x ! a. Поэтому мы имеем равенство

a0 + a1(x a) + + an(x a)n + o((x a)n) =

§ 5.10 РЯД ТЕЙЛОРА

Выражение z0 + z1 + z2 + , где zk – числа, зависящие от натурального индекса k (k = 0; 1; 2; : : : ), называется рядом.

90

Пусть функция f имеет в U(a) производные сколь угодно

высокого порядка. Тогда для нее чисто формально можно записать ряд

Ряд Тейлора может сходиться или расходиться для данных значений x и a. Особенно важен случай, когда ряд Тейлора функции f сходится к самой функции, т. е. S = f(x).

1

Теорема. f(x) = P k1!f(k)(a)(x a)k; x 2 E, тогда и только

k=0

тогда, когда остаточный член Rn(x) в формуле Тейлора f(x) =

n 1

P k1!f(k)(a) (x a)k + Rn(x) = Sn(x) + Rn(x) стремится к нулю

k=0

при n ! 1 (Rn(x)!0)8 x 2 E.

Доказательство. Пусть Rn(x) ! 0 при n ! 1. Тогда из

lim Sn(x) = f(x). Но тогда, так как f(x) = Sn(x) + Rn(x),

n!1

получается, что Rn(x) ! 0 при n ! 1. Замечание. На основании доказанной теоремы и формул

Тейлора для элементарных функций (см. § 5.8) мы можем

91

сделать заключение о справедливости следующих разложений в ряды Тейлора:

1.ex = 1 + x + x2!2 + x3!3 + ; x 2 R.

2.sin x = x x3!3 + x5!5 ; x 2 R.

3.cos x = 1 x2!2 + x4!4 ; x 2 R.

4.ln(1 + x) = x x2!2 + x3!3 ; x 2 ( 1; 1].

§ 5.11 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ С ПОМОЩЬЮ ПОНЯТИЯ

ПРОИЗВОДНОЙ (ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ НА ОТРЕЗКЕ,

ЛОКАЛЬНЫЙ ЭКСТРЕМУМ)

1. Возрастание и убывание функции на отрезке. Определения:

и дифференцируема на (a; b). Тогда имеет место следующая таблица:

Доказательство. Все импликации (следуют) )k являются

92

1.()1). Пусть f0(z) > 0 для 8 z 2 (a; b). Тогда, если y; x 2 [a; b]

и y > x, то существует z 2 (a; b) такая, что справедливо ( ) и, следовательно, f(y) f(x) = f0(z)(y x) > 0, т. е. функция f строго возрастает на [a; b].

2.()3). Пусть f0(z) = 0 для 8 z 2 (a; b); x0 – фиксированная

точка из [a; b]. Тогда для любого x 2 [a; b] (x 6= x0) существет точка z 2 (a; b) и лежащая между x0 и x такая, что f(x)

f(x0) = f0(z)(x x0). Так как f0(z) = 0, то f(x) = f(x0), что означает: f(x) = const для 8 x 2 [a; b].

3. ()7). Утверждение следует из неравенства f0(x) = f0(x +

0) = lim f(x+h) f(x) 0.

h!0+0 h

4. ()6). Данное утверждение следует из )7. Замечание. Из строго возрастания функции на [a; b] не

следует, что f0(x) > 0 для всех x 2 (a; b).

Например, функция f(x) = x3; x 2 R, строго возрастает,

но f0(0) = 0.

2. Локальный экстремум.

Определение 1. Говорят, что функция f достигает в точке a локального максимума (минимума), если существует

окрестность нуля U(0) такая, что f(a + h) f(a) 0 (f(a + h) f(a) 0) для всех h 2 U(0).

Определение 2. Говорят, что f достигает в точке a

локального экстремума, если f достигает в a локального максимума или минимума.

x Теорема (Ферма). Если функция f достигает в точке x локального экстремума и в ней существует f0(x), то последняя

93

Но в точке a существует f0(a), поэтому f0(a+0) = f0(a 0) = = f0(a) = 0.

Замечание. Условия f0(x) = 0 не достаточно для достижения функцией f в точке x локального экстремума, т. е. может быть, что f0(x) = 0, но функция не достигает локального экстремума в точке x.

Например, функция f(x) = x3 имеет в точке x = 0

производную, равную нулю (f0(x) = 3x2 и f0(0) = 0), но в этой точке нет локального экстремума, так как f(x) f(0) = f(x) 0

при x 0 и f(x) f(0) = f(x) 0 при x 0.

Докажем теоремы, дающие достаточные критерии достижения функций локального экстремума по знаку первой производной (теорема 1) и по знаку второй производной (теорема 2).

Теорема 1. Пусть функция f(x) непрерывна в окрестности точки a U(a) и дифференцируема в проколотой окрестности

точки . Если, при некотором , a U(a) > 0

10. f0(x) 0, для 8 x 2 (a; a + ); f0(x) 0, для 8 x 2 (a ; a), то f(x) имеет в точке a локальный минимум.

20. f0(x) 0, для 8 x 2 (a; a + ); f0(x) 0, для 8 x 2 (a ; a), то f(x) имеет в точке a локальный максимум.

Доказательство. f = f(a + h) f(a) = f0(a + h) h; 0 <

< 1. Пусть U(0) такая окрестность нуля, что, если h 2 U(0), то j hj < .

Рассмотрим случай 10 : h > 0:)(a+ h) 2 (a; a+ ):)f0(a+

h) 0: ) f 0; h < 0: ) (a+ h) 2 (a ; a): ) f0(a+ h) 0: ) f 0. Таким образом, существует окрестность нуля U(0) такая, что при h 2 U(0) f 0. Следовательно, f имеет в точке a локальный минимум.

Аналогично доказывается случай 20. Теорема 2. Если функция f удовлетворяет условиям

f0(a) = 0 и f00(a) > 0 (f00(a) < 0), то x0 есть точка локального минимума (максимума) функции f.

знак 0 совпадает со знаком 2 , и поэтому f (a + h) h (h U(0))

0 для 8 2 , т. к.

f(a + h) f(a) = f (a + h) h 0 h U(0) 0 <

94

< 1. Следовательно, функция f имеет в точке a локальный минимум. Вторая часть утверждения теоремы доказывается аналогично.

Замечание. Необходимым условием достижения функцией в точке локального экстремума является несуществование производной в этой точке или равенство ее нулю.

Действительно, если f достигает в точке a локального экстремума и если в a существует f0, то по теореме Ферма f0(a) = 0. Остается случай, когда f достигает в a локального экстремума, но при этом f0 в a не существует. Заметим, что такое возможно, например, для функции, эскиз графика которой имеет вид

y

6

0a -x

(функция имеет в точке локальный максимум, но не имеет производной).

При исследовании на экстремум полезна следующая таблица (f(x); x 2 (c; d); – непрерывна на (c; d); a 2 (c; d)):

95

§ 5.12 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ С ПОМОЩЬЮ ПОНЯТИЯ

ПРОИЗВОДНОЙ (ВЫПУКЛОСТЬ, ТОЧКИ ПЕРЕГИБА)

Пусть y = f(x); x 2 E; – кривая (график функции f(x)); L – секущая, проходящая через точки a; b 2 . Тогда, если при b ! a секущая L занимает единственное предельное положение L0, то прямая L0 называется касательной к кривой в точке a. (см. Рис.)

Рассмотрим три случая:

1 сл. f0(a) – существует (имеет конечное значение). Тогда уравнение касательной имеет вид: y f(a) = f0(a)(x a), где

y = f(x).

2 сл. f(x) – непрерывна в точке a, f0(a) = 1. Тогда уравнение касательной: x = a.

96

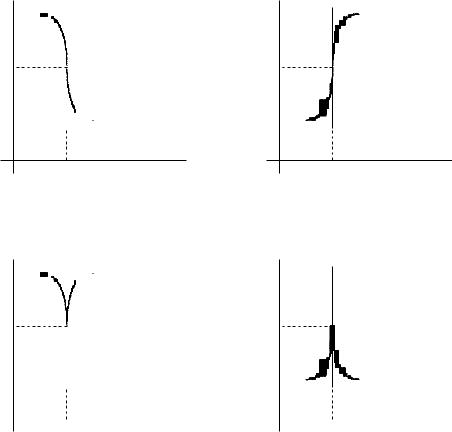
3 сл. f(x) – непрерывна в точке a; f0(a) - не существует. Тогда уравнение касательной: x = a.

Тогда a в третьем случае называется точкой возврата. Определение 1. Пусть в точке a существует конечная f0,

тогда кривая (график функции y = f(x)) выпукла вверх (вниз) в точке a, если кривая в некоторой окрестности U(a) лежит под (над) касательной к кривой в точке a.

Определение 2. Пусть f(x) непрерывна в точке a и

существует конечная f0(a) или f0(a) = 1. Тогда, если для некоторого > 0 в интервалах (a; a + ); (a ; a) кривая (график функции y = f(x)) находится по разные стороны от касательной к кривой в точке a, то точка a называется точкой перегиба кривой.

97

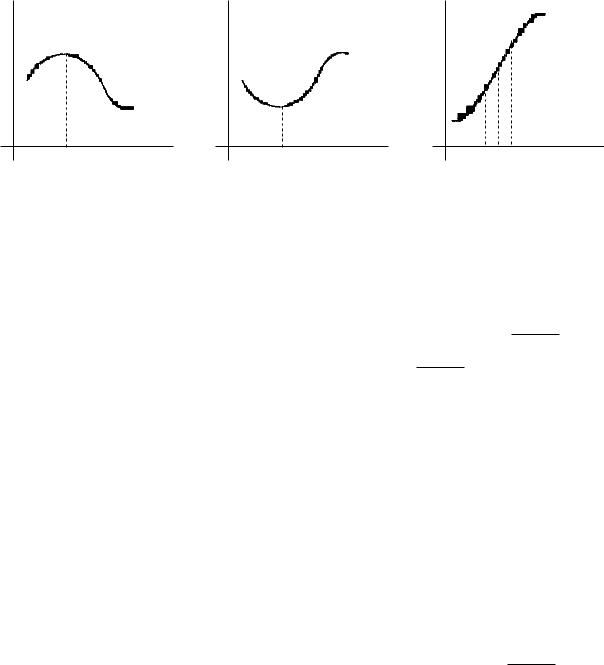
Иллюстрации:

Теорема 1. Если функция f(x) имеет в точке a вторую

проивзодную и f00(a) > 0 (f00(a) < 0), то кривая (график функции y = f(x)) выпукла вниз (вверх) в точке a.

Доказательство. Утверждение теоремы следует из представления: f(x) = f(a) + f0(a)(x a) + (x 2a)2 f00(a +

(x a)); 0 < < 1. Остаток r2(x) = (x a)2 f00(a + (x a))

характеризует превышение кривой над 2касательной y = f(a) + f0(a)(x a). Если f00(a) > 0, то в силу непрерывности f00

вточке a функция f00 сохраняет знак в некоторой окрестности точки a и, следовательно, кривая в некоторой окрестности точки a находится над касательной, т. е. кривая выпукла вниз

вточке a.

Случай f00(a) < 0 доказывается аналогично. Теорема 2. Если функция f(x) такова, что производная f000

непрерывна в точке a, а f00(a) = 0 и f000(a) 6= 0, то кривая (график функции y = f(x)) имеет в точке a точку перегиба.

Доказательство. Утверждение теоремы следует из

представления: f(x) = f(a) + f0(a)(x a) + (x a)3 f000(a +(x a)); x 2 U(a); 0 < < 1. f000 сохраняет знак в3!некоторой

окрестности точки a, и множитель (x a)3 имеет нечетную степень, поэтому кривая (график функции y = f(x)) будет находиться по разные стороны касательной в окрестности точки a. Следовательно, a – точка перегиба кривой.

Теорема 3. Пусть функция f обладает следующими

свойствами:

f00(x0) = = f(k)(x0) = 0;

98

fk+1(x) – непрерывна в точке x0, и f(k+1)(x0) 6= 0.

Тогда, если k – нечетное число, то кривая y = f(x) выпукла вверх или вниз в точке x0 в зависимости от того, будет ли

f(k+1)(x0) < 0 или f(k+1)(x0) > 0, а если k – четное число, то x0 есть точка перегиба кривой.

Если дополнительно к приведенным условиям добавить

ещё

x0 максимума или минимума в зависимости от того, будет ли

f(k+1)(x0) < 0 или f(k+1)(x0) > 0.

Доказательство. По условию f(k+1) непрерывна x0.

Следовательно, f(k+1) определена в некоторой U(x0), и,

следовательно, f(k) – непрерывна в U(x0). Мы получили, что для f выполняются условия разложения по формуле Тейлора

1сл. (k – четное число, f(k+1)(x0) > 0). f(k+1) – непрерывна

вточке x0, поэтому она сохраняет знак в некоторой окрестности точки x0 и, следовательно, f(k+1)(x0 + (x x0)) > 0 для любых

x 2 U(x0). Множитель (x x0)k+1 имеет нечетную степень и поэтому меняет знак при переходе из левой окрестности точки

и, следовательно, кривая y = f(x) будет находиться по разные

стороны касательной к кривой в точке x0, т. е. имеет в точке

x0 перегиб (здесь мы учли, что f(x) = f(x0) + (x x0)f0(x0) – уравнение касательной к кривой y = f(x) в точке x0 ).

99

Иллюстрация:

2 сл. (k – четное число, f(k+1)(x0) < 0). Рассуждая, как и в

100

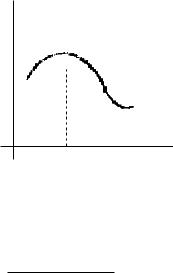
4 сл. (k – нечетное число, f(k+1)(x0) < 0). Очевидно в этом

случае, для всех 2 , и, следовательно,

Rk+1(x) < 0 x U(x0)

кривая y = f(x) будет выпукла вверх в точке x0. Иллюстрация:

y

6

PPPP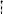PP

При дополнительном условии ( ) разложение (1) примет

вид:

Если k – нечетное число и f(k+1)(x0) > 0 (f(k+1)(x0) < 0), то

мы получим из (2), что f(x) f(x0) 0 (f(x) f(x0) 0) для любых x 2 U(x0), и, следовательно, функция f(x) достигает в

точке x0 локального минимума (максимума).

Если же k – четное число, то нетрудно увидеть, что в точке x0 будет перегиб. Единственное отличие от случаев 1 и 2 будет состоять в том, что касательная к кривой в точке x0 будет параллельна оси абсцисс.

101