§1.2 ПОНЯТИЕ ФУНКЦИИ

I.Определение функции.

Пусть E и F – два множества.

Определение. Функцией, определенной на E со значениями

в F (или отображением E в F ), называется правило f, которое каждому элементу x 2 E относит (единственный) элемент F , обозначаемый f(x).

Обозначение: f : E ! F .

Множество E называется областью определения функции f, а множество F – областью её значений.

Множество G, состоящее из элементов y = f(x), где x 2 E, называется образом множества E при отображении (или

при помощи функции) f. Кратко это записывается так: G = = ff(x)jx 2 Eg. Часто для G используется обозначение G = f(E). Очевидно, образ множества E при отображении f : E ! F является частью множества F , т. е. G F .

II. Счетные множества.

Определение 1. Отображение f : E ! F называется биекцией, если

1.x 6= y(x; y 2 E) ) f(x) 6= f(y)

2.f(E) = F .

(Здесь и в дальнейшем двойная стрелка ")"означает слово "следует".)

Определение 2. Множества E и F называются равномощными, если существует биекция f : E ! F .

Определение 3. Множество E называется счетным, если

оно равномощно множеству натуральных чисел N.

Пример. Множество всех рациональных чисел Q счетно.

9

Доказательство. Q можно представить в виде таблицы

Искомая биекция f : N ! Q может быть определена правилом:

f(1) = 0; f(2) = 1=1; f(3) = 1=1; f(4) = 1=2; f(5) = 1=2; : : :

(встречающиеся ранее числа в дальнейшей нумерации не учавствуют). Таким образом, Q равномощно N.

Упражнения.

Доказать следующие утверждения:

1.Всякое подмножество счетного множества конечно или счетно.

2.Объединение любого конечного или счетного множества счетных множеств есть снова счетное множество.

3.Всякое бесконечное множество содержит счетное подмножество.

Литература: [1], с. 23 – 24.

III.Числовые функции.

Мы будем иметь дело в основном с числовыми функциями: E R; F = R (R – множество действительных чисел).

Числовые функции удобно изображать графиками. В связи с этим говорят о двух переменных: x – независимая переменная (пробегает E), y = f(x) – зависимая переменная. Отсюда возникает обозначение для числовой функции f : E ! R :

y = f(x); x 2 E. Примеры.

1. y = x2; x 2 R.

10

p

2. y = 1 x2; 1 x 1.

8 1; если x > 0;

<

3. y = sgn x = 0; если x = 0;

: 1; если x < 0:

4.y = [x]; x 2 R; [x] – наибольшее целое число x (целая часть числа x).

5.y = fxg = x [x]; x 2 R; fxg – дробная часть числа x.

графически.

Например, функция y = x2 (x 2 R) задается формулой; функция sgn x не может быть задана единственной формулой, т. е. не задается аналитически; функция Дирихле

не может ни быть задана аналитически, ни изображена графически.

IV. Числовая последовательность.

Определение. Последовательностью в R (числовой

последовательностью) называется функция x : N ! R. Обозначение: x1; x2; x3; : : :, или, короче, (xn). Числа xn называются членами последовательности. Последовательности часто задаются формулой общего члена или рекуррентным соотношением.

Примеры.

1.xn = n2; (n 2 N) : 1; 4; 9; : : :

2.xn = ( 1)n; (n 2 N) : : : : ; 1; 1; 1; 1; : : :

3.xn+1 = xn 1 + xn; x1 = x2 = 1 : 1; 1; 2; 3; 5; : : :

4.3; 1; 4; 1; 5; : : : – последовательность цифр в десятичной записи числа (аналитической формулы нет, рекуррентного соотношения тоже нет).

11

V. График функции.

Определение. Графиком функции f : E ! R(E R)

называется часть числовой плоскости =f(x; f(x))2R2jx 2 Eg. Пусть на плоскости R2 задана прямоугольная система координат xy и пусть под кривой на плоскости понимается

просто непустое подмножество R2.

Теорема. Кривая на плоскости R2 является графиком

некоторой функции f : E ! R(E R) тогда и только тогда, когда каждая прямая, параллельная оси OY , пересекает не более чем в одной точке.

Доказательство. Необходимость. Пусть является

графиком функции f : E ! R, т. е. = f(x; f(x)) 2 R2jx 2 Eg. Так как f – функция, то каждому x 2 E соответствует

единственное значение y = f(x), поэтому прямая, параллельная

функции f. Областью определения искомой функции будет множество E = fx 2 Rjпрямая, параллельная оси OY , проходящая через точку (x; 0), пересекает g. Примем теперь за f(x) (значение в точке x искомой функции) ординату точки пересечения прямой, k оси OY с . Тем самым мы установим закон соответствия между x и f(x) такой, что каждому значению x соответствует единственное значение f(x). Таким образом, функция, графиком которой является , определена. Действительно, в этом случае = f(x; f(x)) 2 R2jx 2 Eg.

График определяет функцию y = f(x) (x 2 E). Действительно, если x 2 E, то соответствующее значение y = f(x) определяется как ордината точки (x; a) 2 . Таким образом, при помощи графика задается вполне определенное правило соответствия между x и f(x).

Примеры различных кривых.

1.

12

Кривая является графиком функции (в точке x = a она будет просто не определена).

2.y

6

0

- x

Кривая не будет графиком какой-либо функции, так как в точке x = 0 она принимает два значения.

3.y

6

0a - x

Кривая будет графиком функции (в точке x = a она принимает значение f(a) = b).

4.y

6

0a - x

Кривая не будет графиком какой-либо функции, так как в точке x = a она принимает бесконечное множество значений.

Замечание. Если правило ставит в соответствие каждой точке x 2 E не единственную точку y 2 F , то оно называется многозначной функцией. Примером такой функции

13

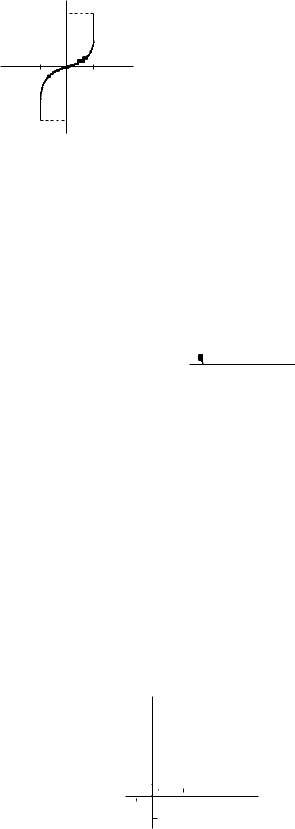
однозначно. Например, в случае y = Arcsin x выделяется y = arcsin x.

VI. Полярная система координат.

В полярной системе координат каждая точка A плоскости характеризуется парой чисел (r; '), где r – расстояние от A до начальной точки O (полюса полярной системы координат), а '

– угол наклона отрезка oA к отмеченному лучу (полярной оси), выходящему из точки 0 (луч ' = 0).

В прямоугольной системе координат соответствие между точками плоскости и парами чисел было биекцией. В полярной системе координат соответствие между точками плоскости и парами (r; ') уже не является биекцией. Например, (0; 0) = = (0; ') при любом '; (r; ') = (r; ' + 2 ) при любых r; '.

Функцию r = r('), заданную на множестве E(' 2 E), можно представить как множество точек (r; ') числовой плоскости, где ' 2 E; r = r('). Многие кривые на плоскости могут быть описаны в полярных координатах с соответствующими функциями r = r(') (однозначными или многозначными).

Примеры. 1. r = '(' 0).

6

14

2. r = r0= cos(' '0); ' 2 ('0 2 ; '0 + 2 ); r0 > 0.

Такая функция описывает в полярных координатах такую прямую, что спущенный на неё из полюса O перпендикуляр имеет длину r0 и образует с полярной осью угол '0.

VII. Обратная функция.

Пусть кривая является графиком функции y = f(x) (x 2 E; y 2 F ). Если кривая определяет x как функцию y, т. е. каждому y ставится в соответствие с помощью (см. рис. 1) единственная точка x, то говорят, что определена x = g(y) (y 2 F ) – функция, обратная к функции f.

6

y'(x; y)

0 x - x

Рис. 1.

Замечание. Графиком обратной функции x = g(y); y 2 F является кривая 0, являющаяся зеркальным отображением кривой относительно биссектрисы I и III координатных углов.

Доказательство. = f(x; f(x)) 2 R2jx 2 Eg. Графиком

обратной функции x = g(y); y 2 F будет следующая кривая

0 = f(y; g(y)) 2 R2jy 2 F g = f(y; x) 2 R2jy 2 F g. Отсюда следует справедливость замечания.

Теорема 1. Если y = g(x) (x 2 F ) – функция, обратная к функции y = f(x) (x 2 E), то справедливы два тождества:

x g(f(x)) (x 2 E); x f(g(x)) (x 2 F ).

Доказательство. Пусть x 2 E ) (x; f(x)) 2 )

) (f(x); x) 2 0 ) x = g(f(x)). Так как x произвольно, то доказана справедливость первого тождества. Второе тождество доказывается аналогично.

15

Теорема 2. Критерий существования обратной функции

будет строго возрастать или, соответственно, строго убывать. Доказательство. Пусть функция f : E ! R строго

возрастает. Покажем, что тогда существует функция, обратная к функции f, и что она будет так же строго возрастать. Для этого нужно показать, что кривая , являющаяся графиком функции f, определяет x как функцию y(y 2 F ). Это будет выполняться, если любая прямая k оси OX пересекает кривуютолько в одной точке. Допустим, что этого нет и что какаято прямая, k оси OX, пересекает кривую в двух точках. Следовательно одному значению y соответствуют два значения x : x1 и x2 (для определенности положим x1 < x2), что означает: f(x1) = f(x2) при x1 < x2. Мы пришли к противоречию с условием строгого возрастания функции f. Таким образом, наше предположение, сделанное выше, является неверным, и, следовательно, любая прямая, k оси OX, пересекает только в одной точке. По определению это означает, что определена функция x = g(y) (y 2 F ) – обратная к функции f. Обратная функция x = g(y) (y 2 F ) будет строго возрастать, так как из

y1 = f(x1) < y2 = f(x2) ) x1 < x2 (в противном случае мы получим противоречие строгому возрастанию функции f).

В случае строгого убывания функции f теорема доказывается аналогично.

Примеры.

p

1. Функция y = 1 x2 ( 1 x 1); y 0, обратной по отношению к себе функции не имеет, так как не является ни строго возрастающей, ни строго убывающей.

III координатных углов. (см. рис.)

16

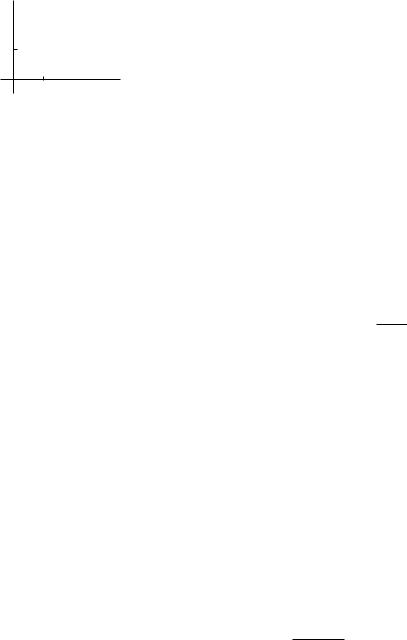
y

6

1 $.

Рис.

VIII. Операции над функциями.

1. Арифметические операции. Пусть f : E ! R; g : E ! R

заданы на одном и том же множестве E R. Тогда можно определить новые функции:

сумма (разность) f g : E ! R по правилу (f g)(x) =

= f(x) g(x); x 2 E,

произведение f g : E!R по правилу (f g)(x)=f(x)g(x); x 2 E, частное f=g : E ! R по правилу (fg )(x) = fg((xx)); x 2 E0, где

E0 = fx 2 Ejg(x) 6= 0g. Замечания.

1. Так как функции принимают числовые значения, то для них справедливы (верные для чисел) коммутативный, ассоциативный и дистрибутивные законы: f + g = g + f;

fg = gf; (f + g) + ' = f + (g + '); (fg)' =

= f(g'), f(g + ') = fg + f'.

2.Если функции f и g определены на разных множествах E1 и E2, то сумма (разность), произведение будут определены на множествах E1 TE2, а функция f=g определена на множестве E1 TE2 TE0

p

Пример. f(x) = 2x2 + 3; g(x) = x 1: f + g; f g; f g

определены для всех x 1, а f=g определена при x > 1.

2. Суперпозиция функций. Пусть f : E ! R; g : F ! R,

причем образ f(E) множества E при отображении f содержится в области определения функции g(f(E) F ). Тогда равенством h(x) = g(f(x)); x 2 E, определяется новая функция h : E ! R, которая называется суперпозицией функции f и g и

обозначается h = g f.

Замечание. Область определения функции g f совпадает с областью определения функции f. Функция h = g f называется также сложной функцией.

17

ине определена при x < 1. Функция (g f)(x) = pf(x) 1 = p

=2x2 + 2

§1.3 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.определена при всех .

СВОЙСТВО НЕПРЕРЫВНОСТИ ДЕЙСТВИТЕЛЬНЫХ

ЧИСЕЛ

В школьном курсе математики дается определение действительных чисел и рассматриваются некоторые их свойства, но среди свойств действительных чисел, не рассматриваемых в школьном курсе, имеются особые свойства, имеющие существенную роль при исследовании числовых функций. К изучению таких свойств действительных чисел мы и приступаем сейчас.

Определение 1. Неотрицательным действительным числом

называется произвольная десятичная дробь вида a = = a0; a1a2 : : : ; где a0 – неотрицательное целое число, отделенное от остальных членов запятой; остальные члены ai – цифры (ai 2 f0; 1; : : : ; 9g; i 1), причем в этой последовательности цифр нет "хвоста" , целиком состоящего из девяток.

Множество всех неотрицательных действительных чисел обозначим R+.

По определению положим 0 = 0; 00 : : :.

Определение 2. Отрицательным действительным числом

=a0; a1a2 : : : , b = b0; b1b2 : : : считаются равными между собой тогда и только тогда, когда их знаки одинаковы и ak =

=bk(k = 0; 1; : : : ).

20. Если a и b положительны, то считается a < b (или, что все равно, b > a), если a0 < b0 или если найдется индекс l такой,

18

что ak = bk(k = 0; 1; : : : ; l) и al+1 < bl+1.

30. Если a положительно (отрицательно), то считается, что a > 0 (a < 0). Если a < 0; b > 0, то, считается, a < b. Если a < 0; b < 0 и jaj > jbj, то считается, что a < b.

Упражнения.

Изучить определение арифметических операций для действительных чисел.

Литература:[2], с. 46 – 49 (§2.3).

1.Свойство порядка действительных чисел.

1.Для каждой пары действительных чисел a и b имеет место одно и только одно соотношение a = b; a > b; a < b.

2.Из a < b и b < c ) a < c (транзитивность).

3.Если a < b, то существует действительное число c такое, что a < c < b.

Доказательство. Свойства 1 и 2 вытекают непосредственно

из определений знаков "=" и "<". Пусть 0 a = = a0; a1a2 : : : < b = b0; b1b2 : : : и an < bn. Положим тогда

Очевидно, что a < c < b.

Если a < 0; b 0 или a < 0; b < 0 (a < b), то следует рассмотреть случаи jaj > b или jaj > jbj, для которых существование числа c мы доказали. Искомое нами число будет равно c.

2.Архимедово свойство действительных чисел.

Для любого действительного числа a > 0 существует натуральное число n > a.

Действительно, если a = a0; a1a2 : : : , то можно взять n = = a0 + 1.

19

3.Свойство непрерывности множества действительных чисел.

Сформируем ряд понятий, необходимых для определения свойства непрерывности.

такое, что a b (a b) для любого a 2 E, при этом число b называется мажорантой (соответственно, минорантой)

множества E.

Определение 2. Множество, ограниченное сверху и снизу, называется ограниченным.

Определение 3. Наименьшая мажоранта ограниченного сверху множества E называется точной верхней гранью E и обозначается одним из символов: sup E; sup a (supremum

a2E

– наивысшее).

Данное определение можно привести в другой записи: "c является sup E, если удовлетворяет двум условиям:

1.c – мажоранта E.

2.Любое число d < c уже не является мажорантой E".

Аналогично, точная нижняя грань ограниченного снизу

множества E есть наибольшая миноранта множества E. Обозначение: inf E; inf a (infimum – наинизшее).

a2E

Свойство непрерывности действительных чисел: "Непустое

ограниченное сверху (снизу) множество действительных чисел имеет точную верхнюю (точную нижнюю) грани".

Доказательство. Ограничимся случаем, когда E R+,

и доказательством существования sup E. E ограничено сверху. Следовательно, E имеет мажоранту, в качестве которой можно взять натуральное число n0:

a = a0; a1a2 n0; 00 : : : для любого a 2 E:

Пусть c0 – наибольшее из целых чисел, стоящих до запятой у чисел множества E. Тогда c0 n0. Пусть E0 – часть E, состоящая из чисел, у которых до запятой стоит c0:

E0 = fc0; a01a02 : : : ; c0; a001a002 : : : ; : : : g:

20

Пусть c1 – наибольшая из цифр, стоящих на первом месте после запятой у чисел множества E0, так что c1 9. Пусть E1 – часть E0, состоящая из чисел, у которых на первом месте после запятой стоит c1. Продолжая этот процесс, мы приходим к выражению

c0; c1; c2; : : : ( )

Пока нельзя утвеждать, что записано действительное число, так как в ( ) может оказаться хвост из девяток. Положим

Покажем, что – мажоранта E. Пусть a = a0; a1a2 : : : 2 E. Рассмотрим два случая:

мажорантой множества E. Действительно, пусть d <

(d = d0; d1d2 : : : ). Тогда найдется такое n, что di = ci при всех i < n, но dn < cn. Отсюда следует, что любое число

a 2 En будет больше d, так как ai = ci = di при всех i < n и an = cn > dn. Таким образом, d не может быть мажорантой

E, и, следовательно, – наименьшая мажоранта E.

Упражнения.

1.Доказать существование sup E для произвольного непустого E R, ограниченного сверху.

2.Доказать существование inf E для произвольного непустого E R, ограниченного снизу.

Указание: Предварительно доказать две леммы:

Лемма 1. Любое непустое множество E R+ имеет точную нижнюю грань.

21