Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

kniga1.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.54 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Аналогично определяется дифференциал n-го порядка (по индукции): dnf(x) = d(dn 1f(x)) = d(fn 1(x)dxn 1) =

f(n)(x)dxn.

Из данного равенства следует f(n)(x) =

d f(x)

dxn

Докажем формулу, по которой вычисляется производная

n-го порядка от произведения двух функций.

–

функции,

Формула Лейбница:

Пусть

U; V

обладающие n-й производной

в точке

Тогда

(считая

по

определению, U(0)(x)

U(x);

V (0)(x)=V (x))

имеем

k k

(U(x)V (x))(n)=P CnU(

)(x)V ( )(x), где

; k =

k!(n k)!

k=0

0; 1; : : : ; n; – биноминальные коэффициенты (см. [2], § 5.9, с. 145).

Доказательство.

Проводится

по

индукции.

При

формула очевидна. Предположим,

что

она

верна

для

случая

n-й

производной.

Тогда

(U(x)V (x))(n+1)

CkU(k)(x)

V (n k)(x)

(n kP)

(k+1)

(k)

(n k+1)

k=0

n+1

Cn [ U

(x)V (x)+U (x)V

(x)]

Pk 1 (k)

(n+1 k)

k (k)

(n+1 k)

k=0

Cn U (x)V

(x) +

CnU (x)V

(x)

P k

(k)

(n+1 k)

k=1

k=0

n+1

(x), так как Cn+1 =

Cn+1U (x)V

Cn =

P= 1 Ck

= Ck

+ Ck 1; k = 1; : : : ; n

k=0

n+1

Пример. (x sin x)(100) = C1000 x(sin x)(100)+C1001 x0 (sin x)(99) =

x sin(x + 100 2 ) + 100 sin(x + 99 2 ) = x sin x 100 cos x.

§ 5.5 ОСНОВНЫЕ ТЕОРЕМЫ

Теорема Ролля. Пусть f : [a; b] ! R непрерывна и

дифференцируема в (a; b), причем f(a) = f(b). Тогда существует точка c 2 (a; b) такая, что f0(c) = 0.

Доказательство. Если f(x) – постоянная на [a; b], то теорема

очевидна. Пустьf(x) 6= const и существует точка x 2 (a; b) такая, что, например, f(x) > f(a). Тогда ("непрерывная на [a; b]

функция достигает своих точных граней" ) существует точка c 2 (a; b) такая, что f(c) = max f(x). Отсюда следует

x2[a;b]

f0(c + 0)=

lim

f(c + h) f(c)

0; f0(c

0) =

0+0

lim

f(c + h) f(c)

(

)

0 0

Так как f(x) дифференцируема в точке c, то f0(c + 0) =

f0(c 0) и из ( ) следует f0(c) = 0.

! R; g

Теорема Коши (о среднем). Пусть f

: [a; b]

[a; b] ! R непрерывны на [a; b], причем f и g дифференцируемы на (a; b); f0(x); g0(x) 6= 0 одновременно и g(b) 6= g(a). Тогда

существует точка c 2 (a; b) такая, что f(b) f(a) = f00(c).

g(b) g(a) g (c)

Доказательство. Рассмотрим функцию h(x) = g(x) [f(b)

f(a)] f(x) [g(b) g(a)]; a x b. Нетрудно проверить, что h(a) = h(b). Очевидно также, что h(x) непрерывна на [a; b] и дифференцруема на (a; b). Таким образом, функция h(x) удовлетворяет условиям теоремы Ролля, и, следовательно, существует c 2 (a; b) такое, что

h0(c) = g0(c) [f(b) f(a)] f0(c) [g(b) g(a)] = 0:					( )
Очевидно, что	g0	6 , иначе будет	f0	, что противоречит
		(c) = 0		(c) = 0

предположению теоремы. Поэтому из ( ) следует искомое равенство.

Теорема (формула Лагранжа конечных приращений).

Пусть f:[a; b] ! R непрерывна на [a; b]	и дифференцируема
на (a; b). Тогда существует точка c	2 (a; b) такая, что

f(b) f(a) = f0(c)(b a).

Доказательство. Пусть g(x) из теоремы Коши равна x. Очевидно, f и g будут удовлетворять условиям теоремы Коши.

Из теоремы Коши следует f(b) f(a) = f0(c); c 2 (a; b).

b a

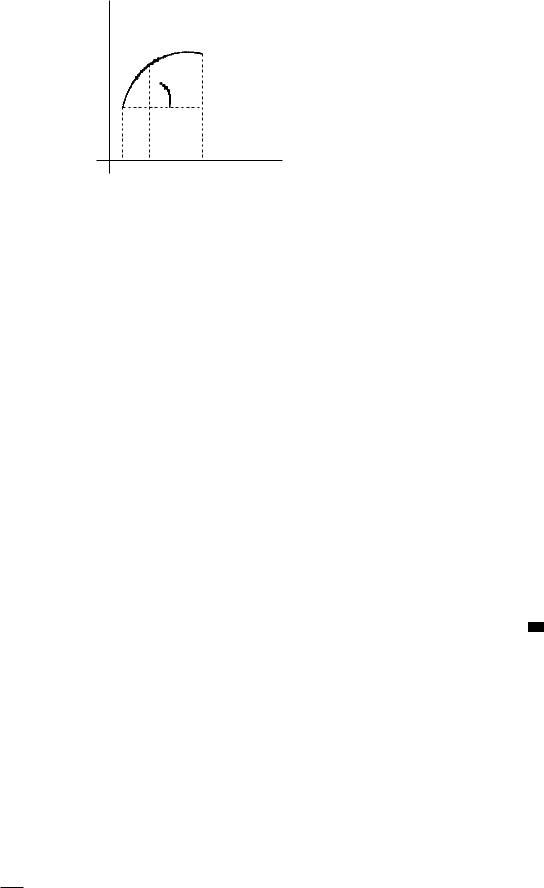
Геометрический смысл формулы Лагранжа

0 a c

-x

	Запишем		равенство из формулы	Лагранжа в виде
	f(b) f(a)	= f0(c);	c 2 (a; b). Левая часть этого равенства есть tg
	b a
( – угол наклона к оси абсцисс хорды,				стягивающей точки

(a; f(a)); (b; f(b)) графика функции f(x)). Правая часть есть тангенс угла наклона касательной к графику в точке c 2 (a; b). Таким образом, формула Лагранжа утверждает, что если f(x) непрерывна на [a; b] и дифференцируема на (a; b), то на кривой, являющейся графиком f(x), существует точка (c; f(c)) такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой (a; f(a)); (b; f(b)).

Теорема 1. Если функция имеет на (a; b) производную,

равную нулю, то она постоянна на (a; b).

Доказательство. Пусть x1 – фиксированная точка из

(a; b); x – произвольная точка из (a; b) (она может находиться справа и слева от x1). Тогда на основании формулы Лагранжа

имеет место f(x) f(x1) = (x x1)f0(c), где c – некоторая, зависящая от x1 и x, точка, находящаяся между x1 и x. По

условию f0(x) 0 на (a; b), поэтому f0(c) = 0 и f(x) = f(x1) =

C const, для любых x 2 (a; b).

§ 5.6 ПРАВИЛО ЛОПИТАЛЯ

Пусть f и g определены и дифференцируемы в некоторой

проколотой окрестности U(a) (a – число или 1; 1), причем

g(x); g0

и выполнено одно из условий

(x) = 0

(a)

x!a

lim f(x) = lim g(x) = 0

x!a

1 или 1

lim f(x) = lim g(x) =

= lim

Тогда, если существует предел lim	f0(x)	(конечный или

x!a g0(x)

бесконечный), то существует также равный ему предел

lim

x!a

f(x)	= lim	f0(x)	.
g(x)
	x!a g0(x)

Правило верно также для случаев: lim ; lim .

x!a+0 x!a 0

Доказательство.Разберем несколько случаев.

1. (0=0); x ! a + 0; a – конечное число. В этом случае под

U(a) понимается правая окрестность точки a, т. е. U(a) = (a; ),

где

Определим

функции f

и g

точке

a :

f(a)=0=

lim f(x); g(a)=0= lim g(x). Тогда

и g

будут

x!a+0

[a; )

. Так

x!a+0

условию,

g0(x) = 0

при

непрерывны

на

как,

по

x 2 (a; ), то g(x) g(a)

6= 0;

< x

< . Мы получили,

что функции f и g удовлетворяют условиям теоремы Коши на отрезке [a; x]; x < . Применяя теорему Коши, получим

f(x)

= f(x) f(a)

= f0(c);

(

)

g(x)

g(a)

(c)

где c 2 (a; x) или c = a + (x a); 0 < < 1.

lim

f(x)

Перейдем в ( ) к пределу при x ! a + 0 :

g(x)

a+0

lim

f0(c)

x!a+0

g0(c)

lim

f0(c)

lim

f0(c)

g0(c)

При x ! a + 0; c ! a + 0, поэтому x!a+0

c!a+0 g0(c) .

Последний предел существует по условию. Таким образом,

lim

f(x)

= lim

f0(x)

g(x)

x!a+0

g0(x)

(0=0); x ! a 0; a – конечное число. Этот случай

доказывается аналогично случаю 1 (сходимости справа).

Отличия состоят только в том, что ;

U(a) = ( ; a); < a

функции f и g удовлетворяют условиям теоремы Коши на отрезке [x; a]; x > .

3.(0=0); x ! a; a – конечное число. Справедливость

правила					двух предыдущих
		в этом случае следует из
случаев.		Действительно,	если	существует		предел
lim	f0(x)	= , то существуют		пределы lim		f0(x)	=
						g0(x)
x!a g0(x)					x!a+0

f00(x) = . Отсюда, согласно случаям 1 и 2, следует,

x!a 0 g (x)

что

существуют пределы

lim

f(x)

lim

f(x)

, что

g(x)

x!a+0

x!a 0

g(x)

равносильно существованию lim

f(x)

= .

x!a

g(x)

4. (0=0); a = 1. Положим y = x1 . Тогда функции F (y) =

f(1),

g(1) дифференцируемы

некоторой

окрестности

G(y)

нуля

U(0)

. (Заметим,

. В этой же

0; G0

: G(y)

(y) =

что если a = +1, то функции F (y); G(y) дифференцируемы в правой окрестности нуля, если же a = 1, то в левой

окрестности нуля.) Далее, lim F (y) =

lim f(x) = 0; lim G(y) =

x!1

f0(x)

f0(y1 ) (

)

F 0(y)

( )

F (y)

= lim g(x) = 0; lim

= lim

g0(x)

g0(1 ) (

)

G0(y)

G(y)

x!1

f(x)

x!1

y!0

= lim

x!1

g(x)

Равенство ( )

справедливо благодаря доказанному выше

случаю 3 ((0=0); a = 0).

5. (1=1). Будем считать, для определенности, что a – конечное число и что x ! a + 0.

В этом случае . Пусть

U(a) = (a; ); > a

lim (f0(x)=g0(x)) = .

x!a+0

Допустим также, что x и такие, что [x; ] (a; ). Тогда,

с учетом теоремы Коши для отрезка [x; ], имеем

f(x)

f(x)[g( ) g(x)]

f( ) f(x)

g(x)

g(x)[f( )

f(x)] g( )

g(x)

f(x)g(x)

(g( )=g(x)) 1

f0(c)

;

g(x)f(x) (f( )=f(x)) 1

g0(c)

где c 2 (x; ). Параметром в правой части данного равенства мы можем распоряжаться. Выберем его немного позднее.

lim f00(x) существует, поэтому по критерию Коши:

x!a+0 g (x)

8" > 0(пусть " < 1)9 1	> a8x; y 2	(a; 1)		f (y)	f (x)	<	"	:
8" > 0(пусть " < 1)9 1	> a8x; y 2	(a; 1)	g00(y)		g00(x)	<	3	:

В силу условия x

a+0

1 имеем

lim f(x) =

lim g(x) =

lim

(g( )=g(x)) 1

= 1; поэтому

(f( )=f(x)) 1

x!a+0

1 1

< 3 :

9 2 > a 8 x 2 (a; 2)

(f( )=f(x))

(g( )=g(x))

(g( )=g(x)) 1

Введем

обозначения:

h( ; x)

(f( )=f(x)) 1

lim h( ; x)

f0(x)

lim

h( ; x)

lim

(f0(x)=g0(x)) = , поэтому

g0(x)

x!a+0

9 3 > a 8 x 2 (a; 3)

h( ; x)g00(x) <

f (x)

Возьмем

качестве

min( 1;

2; 3)

запишем

0(c) f

(c)

0(c)

0(x)

8 f

(x)

0(x)

(f(x)=g(x))

в следующем виде: для

2 (a; )

f(x)

g(x)

= h( ; x)g

h( ; x)g

+h( ; x)g

)

(

)

(

)

0( )

f0(c)

f0(x)

f0(c)

f0(x)

(h( ; x)

+ h( ; x)

)

(

f0(c)

f0(x) f0(c)

f0(x)

h( ; x)

+ h( ; x)

)

g x

)

(

0( )

(a; )

> c

f(x)

(x)

(Заметим, что

число

Таким образом,

lim

= =

lim

g(x)

(x)

x!a+0

Упражнения.

Доказать случаи правила Лопиталя: (1=1); x ! a 0; a – конечное число; (1=1); x ! a; a – конечное число;

(1=1); x ! 1; (1=1); x ! +1;

(1=1); x ! 1.

Указание: использовать приемы доказательства случаев 2

– 4.

Замечание 1. В	условиях			правила Лопиталя из
существования предела	lim	f(x)	,	вообще говоря, не следует

	x!a	g(x)

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.09.2019155.65 Кб2Kitay_16-17_vv.doc
#
13.08.2019516.1 Кб68Klassichesky_lechebnyy___massazh.doc
#
17.11.2019104.45 Кб1kleiner Mann 1.doc
#
09.11.201886.53 Кб3kleiner Mann 1.doc
#
10.02.201531.71 Mб17Klientov_A_E_-_Narodnye_promysly_Istoria_Ross.pdf
#
10.02.20151.54 Mб48kniga1.pdf
#
12.09.201916.9 Mб4kniga_h-s.doc
#
18.08.2019142.85 Кб10kodeks-ESOMAR.doc
#
10.02.20156.82 Mб57Kogogin D.A .(RINEX) (Секция 1).rtf
#
22.12.2018310.51 Кб3Kollokvium.docx
#
29.08.2019253.95 Кб1kommer.doc