
- •МНОЖЕСТВА И ФУНКЦИИ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
- •1.2 ПОНЯТИЕ ФУНКЦИИ
- •1.4 ТОПОЛОГИЯ ЧИСЛОВОЙ ПРЯМОЙ. РАСШИРЕННАЯ ЧИСЛОВАЯ ПРЯМАЯ
- •ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.1 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.2 ЛЕММА О ВЛОЖЕННЫХ ОТРЕЗКАХ. ТЕОРЕМА ВЕЙЕРШТРАССА
- •2.3 МОНОТОННЫЕ ОГРАНИЧЕННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- •2.4 КРИТЕРИЙ КОШИ
- •ПРЕДЕЛ ФУНКЦИИ
- •3.1 ПРЕДЕЛ ФУНКЦИИ. СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИИ. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •3.2 КРИТЕРИЙ КОШИ СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ
- •3.3 МОДИФИКАЦИЯ ПОНЯТИЯ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ
- •3.4 ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •3.5 ПОРЯДОК ФУНКЦИИ. ЭКВИВАЛЕНТНОСТЬ (АСИМПТОТИКА)
- •НЕПРЕРЫВНЫЕ ФУНКЦИИ
- •4.2 ТОЧКИ РАЗРЫВА
- •4.3 СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •4.4 РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ. ПРОДОЛЖЕНИЕ ПО НЕПРЕРЫВНОСТИ
- •4.5 НЕПРЕРЫВНОСТЬ ОБРАТНОЙ ФУНКЦИИ
- •4.6 ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ. ЛОГАРИФМИЧЕСКАЯ, СТЕПЕННАЯ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- •ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- •5.2 ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- •5.3 ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ
- •5.5 ОСНОВНЫЕ ТЕОРЕМЫ
- •5.6 ПРАВИЛО ЛОПИТАЛЯ
- •5.7 ФОРМУЛА ТЕЙЛОРА
- •5.8 ФОРМУЛА ТЕЙЛОРА ДЛЯ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •5.9 ЛОКАЛЬНАЯ ФОРМУЛА ТЕЙЛОРА
- •5.10 РЯД ТЕЙЛОРА
- •ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •6.3 ОТЫСКАНИЕ ПЕРВООБРАЗНЫХ ДЛЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- •ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •7.2 ВЕРХНИЕ И НИЖНИЕ ИНТЕГРАЛЬНЫЕ СУММЫ
- •7.3 НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
- •7.4 НЕКОТОРЫЕ КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- •7.5 ОСНОВНЫЕ СВОЙСТВА ИНТЕГРАЛА РИМАНА
- •7.6 СВОЙСТВА ИНТЕГРАЛА РИМАНА, В КОТОРЫХ ФИГУРИРУЮТ НЕРАВЕНСТВА
- •7.7 ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА
- •7.8 ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
- •7.9 ОБЩИЕ ПРИЕМЫ ИНТЕГРИРОВАНИЯ
- •7.10 НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛА РИМАНА
- •НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- •8.2 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ОТ НЕОТРИЦАТЕЛЬНЫХ ФУНКЦИЙ
- •8.3 ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
- •8.4 НЕСОБСТВЕННЫЙ ИНТЕГРАЛ И РЯД

jx |
00 |
zj < |
00 |
|
00 |
˜ |
(z)j < "=3: |
(3) |
|||||||
|
|
) jf(x |
) f |
||||||||||||
Действительно, если y; z 2 E F , то (2) и (3) следуют |
|||||||||||||||
из (1), так как |
0 |
и |
˜ |
|
|
|
. Если же˜ |
|
2 |
|
n |
|
, то (2) и (3) |
||
|
|
00 |
< 3 |
|
y; z |
|
F |
|
E |
|
|||||
следуют из того, что f |
(y) = lim f(x); f |
(z) = lim f(x). Выберем |
|||||||||||||
|
|
|
|
|
|
|
|
x!y |
|
|
|
x!z |
|
||
теперь x0 2 U 0(y) TE; x00 2 U 00(z) TE (здесь U 0(y) = (y 0; y+
0); U 00(z) = (z 00; z + 00)) и запишем очевидное неравенство
˜ |
˜ |
|
|
˜ |
|
|
|
0 |
|
|
|
|
0 |
) |
|
|
|
|
00 |
|
|
00 |
|
˜ |
|
jf (y) |
f (z)j |
= jf (y) f(x |
) + f(x |
f(x |
) + f(x |
) f (z)j |
|||||||||||||||||||
|
|
˜ |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
00 |
|
|
|
|
00 |
) |
˜ |
(z)j: |
(4) |
|
|
jf (y) f(x |
)j + jf(x |
) f(x |
)j + jf(x |
f |
|
|||||||||||||||||||
Учитывая, |
|
|
x0 |
|
|
|
2 |
x00j |
|
U |
|
(y) E; |
|
x00 |
y +2 |
||||||||||
U 00(z) |
E |
|
ичточто |
jx0 |
j |
|
|
0 |
|
= T |
|
jx0 |
|
|
|||||||||||
+y zT |
x |
00j j 0 |
|
j |
+ |
y |
|
j |
|
j |
|
|
x |
00j |
< 3 |
, используя (1), |
|||||||||
|
+ z |
|
x |
|
y |
|
|
|
z |
+ z |
|
|
|
|
|
||||||||||
(2), (3), мы получили из (4): 8" > 0 9 > 0 8y; z 2 F (jy zj <
) j˜ ˜ j ). Равномерная непрерывность функции ˜
f (y) f (z) < " f
на F доказана.
§ 4.5 НЕПРЕРЫВНОСТЬ ОБРАТНОЙ ФУНКЦИИ
Пусть y = f(x) – некоторая числовая функция, заданная на множестве E R; F = f(E) – область значений функции f. Функцию, обратную к функции f, мы определяли так: если кривая , являющаяся графиком f, определяет x как функцию y, то говорят, что определена обратная функция x = g(y); y 2 F . Было доказано также, что если f строго возрастает (строго убывает), то обратная функция существует и также строго возрастает (строго убывает).
Рассмотрим теперь вопрос о непрерывности обратной функции.
Теорема 1. Пусть y = f(x) непрерывна и строго возрастает
на [a; b]. Тогда образ [a; b] есть отрезок [A; B] (A = f(a); B = f(b)) и обратная к f функция x = g(y) будет строго
возрастающей и непрерывной на [A; B]. |
|
Доказательство. Прежде всего докажем, что f([a; b]) |
= |
[A; B]. Так как f строго монотонна, то очевидно f([a; b]) |
|
[A; B]. Далее, опять же в силу строгой монотонности, f(a) |
< |
f(b), поэтому (по теореме 4 из § 4.3) для 8y 2 [A; B] 9 x 2 [a; b]
58

такое, что f(x) = |
y, и это означает: y 2 f([a; b]) ) [A; B] |
|||||||||||||||||
f([a; b]). В итоге мы доказали, что f([a; b]) = [A; B]. |
|
|||||||||||||||||
|
|
Таким образом, нам остается доказать, что из |
||||||||||||||||
непрерывности |
f |
|
на |
[a; b] |
следует |
непрерывность g |
на |
|||||||||||
[A; B]. Пусть |
y0 |
|
2 |
[A; B] |
и |
yn |
2 |
[A; B] такие, |
что |
|||||||||
yn |
! y0. Положим x0 |
= g(y0); xn = g(yn). Тогда, из |
||||||||||||||||
свойства |
обратной |
|
функции, |
следует |
y0 |
= |
|
f(g(y0)); yn |
= |
|||||||||
f(g(yn)) |
= |
f(xn). Непрерывность функции |
g в точке |
y0 |
||||||||||||||
будет доказана, если мы покажем, что xn |
! x0. Допустим, |
|||||||||||||||||
что |
это |
не |
так. |
Тогда |
существует |
подпоследовательность |
||||||||||||
|
nk |
! |
x0 |
, |
причем |
x0 |
2 |
|
|
и |
x0 |
6 |
|
0 |
(существование |
|||
x |
|
|
|
|
|
|
|
[a; b] |
|
= x |
|
|
|
|||||
такой подпоследовательности следует из следствия к теореме
Вейерштрасса, т. к. |
|
n |
|
при |
|
). Так как |
|
0 |
6 |
, то |
|||||||
|
x |
|
[a; b] |
|
n |
|
|
1 |
6 |
x |
|
. |
= x0 |
|
nk |
|
|
в силу строгого возрастания функции |
|
: |
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
f |
|
f(x |
) = f(x0) |
|
(f(x |
|
)) |
|||
является подпоследовательностью последовательности (yn), но |
||
yn |
! y0, поэтому f(xnk ) = ynk ! y0 = f(x0). В то же время, |
|
в силу непрерывности f, f(xnk ) ! f(x0), так как xnk ! x0. В |
||
итоге мы получили, что последовательность (f(xnk )) имеет два |
||
различных предела, что невозможно. Таким образом, xn ! x0. |
||
x |
Теорема 2. Пусть f(x) непрерывна и строго возрастает на |
|
(a; b) и пусть A = inf f(x); B = |
sup f(x), причем может |
|
|
x2(a;b) |
x2(a;b) |
быть, что a = 1; A = 1; b = +1; B = +1. Тогда образ (a; b) есть (A; B), и обратная к f(x) функция x = g(y) строго возрастает и непрерывна на (A; B).
Доказательство. Так как f(x) строго возрастает, то
очевидно f((a; b)) (A; B). Покажем обратное включение. Пусть y 2 (A; B), тогда, в силу определения A и B, существуют
x1; x2 2 (a; b) такие, что y1 = f(x1) < y < f(x2) = y2. А так как f(x) строго возрастает, то должно быть x1 < x2. Функция f(x)
непрерывна на (a; b), тем более она непрерывна на [x1; x2] (a; b) ) (по теореме 4 § 4.3) существует единственная точка x 2
[x1; x2] такая, что f(x) = y ) y 2 f((a; b)) ) (A; B) f((a; b)). В итоге: f((a; b)) = (A; B).
Проверим далее, что g(y) непрерывна в любой точке
интервала (A; B). Пусть y |
2 |
(A; B). |
Очевидно функцию |
g(y), считая её определенной |
при y 2 |
[f(x1); f(x2)] можно |
|
рассматривать как функцию, |
обратную |
к функции f(x), |
|
определенной на [x1; x2] (существование точек x1 и x2 мы доказывали выше для любой точки y 2 (A; B)). Так как f(x)
59
непрерывна на [x1; x2], то по теореме 1 g(y) будет непрерывна
на [f(x1); f(x2)], т. е. в точке y 2 [f(x1); f(x2)] (A; B). Точка y
– произвольная точка из (A; B), поэтому g(y) – непрерывна на
(A; B).  Замечание 1. В теоремах 1 и 2 можно заменить
Замечание 1. В теоремах 1 и 2 можно заменить
"возрастающая" |
на "убывающая", и тогда в их заключениях |
|||
надо заменить, |
соответственно, [A; B] на [B; A] и (A; B) |
на |
||
(B; A). |
|
|
(A; B) можно, |
|
Замечание 2. В теореме 2 интервалы (a; b); |
||||
соответственно, |
заменить на полуинтервалы, |
x |
например, |
на |
[a; b); [A; B), и тогда a и A – конечные числа. |
|
|
||
§ 4.6 ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ. ЛОГАРИФМИЧЕСКАЯ, СТЕПЕННАЯ, ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Пусть n 2 N; a 2 R; a > 0. Число an = a : : : a
| {z
{z }
}
n раз
(по определению). Число a1=n – арифметический корень n-й степени из числа a. Если n=m – неотрицательное рациональное
число, то (по определению) полагаем an=m = (a1=m)n = (an)1=m. Таким образом, мы определили функцию f(p) = ap; p 2 Q. Из элементарной алгебры известно, что ap (p 2 Q) обладает свойствами:
1.ap+q = ap aq.
2.ap строго возрастает при a > 1 и строго убывает при
a < 1. |
можно ли доопределить |
функцию |
Возникает вопрос, |
||
f(p) = ap (p 2 Q) на |
иррациональных числах |
так, что, |
определенная уже на всей числовой прямой R, продолженная функция будет непрерывной на R и удовлетворять свойствам 1. и 2. Докажем существование такой функции. Начнем с
того, что докажем равномерную непрерывность |
f(p) = |
ap |
|||
на любом отрезке [ N; N] |
Q; n |
2 |
N. |
Пусть |
для |
определенности a > 1. Если |
T |
2 |
|
T |
, то |
|
p < q (p; q |
|
[ N; N] Q) |
|
|
0 < aq ap = ap(aq p 1) < aN (aq p 1). Пусть " > 0 - произвольное число и n0 2 N такое, что если n > n0, то
ja1=n 1j < " a N |
(1) |
60

(этого можно добиться, так как lim a1=n = 1).
Таким образом, если 0 < q p n0 |
+1, то мы получим, |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
используя (1), что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 < aq ap < aN (a |
|
1) < ": |
|
(2) |
||||||||||
n0+1 |
|
|||||||||||||
Далее, если p > q, то |
|
|
|
|
|
|
|
|
|
|
|
|
||
0 < ap aq = aq(ap q 1) < aN (ap q 1): |
|
|
||||||||||||
Отсюда, используя (1), получим |
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
0 < ap aq < aN (a |
n0+1 |
1) < "; если 0 < p q |
|
: |
(3) |
|||||||||
n0 + 1 |
||||||||||||||
Перепишем (2) следующим образом: |
|
|
|
|
|
|
|
|
||||||
если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
p |
|
q < 0; |
то |
" < ap |
|
aq < 0: |
|
(4) |
|||||
n0 + 1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Из (4) и (3) ) 8p; q 2 [ N; N] TQ справедливо: jp qj
1
n0+1
ap на любом отрезке [ N; N] TQ.
Любая точка R является предельной для множества Q, поэтому на R можно определить функцию f(x) следующим образом:
|
ax; |
если x |
2 Q; |
|
||
(p!x |
если |
|
2 |
n |
|
|
f(x) = |
lim ap; |
|
x |
|
R |
Q: |
Докажем, что это и есть искомая нами функция. Пусть x 2 RnQ. Накроем эту точку некоторым отрезком [ N; N]; N 2 N. Выше была доказана равномерная непрерывность функции ap; p 2 Q на множестве [ N; N] TQ. Так как функция f(x) является продолжением функции ap; p 2 [ N; N] TQ, то по теореме "Продолжение по непрерывности" (см. § 4.4), f(x) будет равномерно непрерывна на [ N; N], а следовательно, просто непрерывна в точке x 2 RnQ. Любая точка x 2 RnQ может быть накрыта отрезком [ N; N], поэтому f(x) будет непрерывна в любой точке x 2 R.
Вновь определенную функцию обычно обозначают f(x) = ax; x 2 R и называют показательной функцией. Докажем
61
справедливость свойств 1. и 2. для показательной функции ax; x 2 R. Пусть x; y 2 RnQ, причем x < y. Существуют рациональные числа p; q такие, что x < p < q < y (см. § 1.3 "Свойства порядка действительных чисел" ). Пусть pn; qn 2 Q такие, что pn ! x (возрастая), а qn ! y (убывая) ) apn < ap < aq < aqn. Переходя к пределу, получим ax ap < aq ay. Таким образом, мы доказали свойство 2. Свойство 1. следует из равенства apn+qn = apn aqn после перехода к пределу.
Если a < 1, то полагаем ax = (1=a1 )x . Функция (1=a)x, по доказанному выше, будет непрерывна на R; (1=a)x > 0 при
x 2 R, поэтому функция ax (a < 1) будет непрерывна на R. Заметим, что при a < 1 функция ax будет строго убывать.
При a = 1 полагаем: 1x = 1 при любом x 2 R.
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
Определение. Функция, обратная к показательной y = ax (x 2 R), a > 0; a 6= 1, называется логарифмической и обозначается y = loga x; x > 0.
|
y |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
y=ax |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y= loga x |
|
|
|
y=ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y= loga x |
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
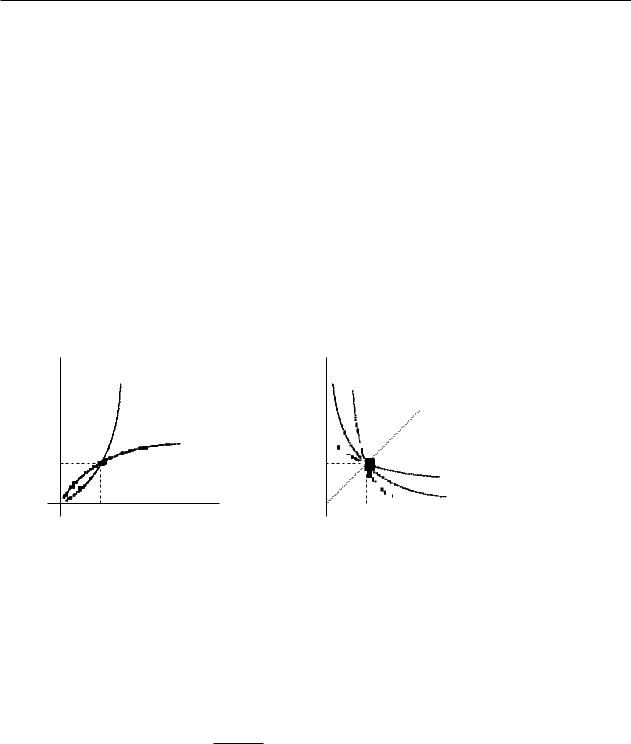
Рис. 1. (a > 1) |
|
|
|
|
Рис. 2. (a < 1) |
||||||||||||||||||||||||||||||||||||||||||||||||
Логарифмическая |
функция будет |
непрерывной, как |
|||||||||||||||||||||||||||||||||||||||||||||||||||
функция, обратная к показательной (непрерывной) функции.
Из свойства обратной функции следует: |
|
|
1. |
aloga x = x (x > 0). |
( ) |
2. |
loga(ax) = x (x 2 R: |
|
Упражнения.
Доказать следующие свойства логарифмической функции:
1.loga xy = loga x + loga y.
2.loga xy = loga x loga y.
3.loga xy = y loga x.
62
4. loga b loga a = 1.
СТЕПЕННАЯ ФУНКЦИЯ
y = xb (b – постоянная, x – переменная, x > 0) – степенная функция.
Согласно свойствам ( ) логарифмической функции
xb = eb ln x(x > 0), ln x – непрерывная функция, показательная функция - непрерывна, суперпозиция двух непрерывных функций есть функция непрерывная, поэтому степенная функция будет непрерывной.
Из xb = eb ln x(x > 0) )
0), а также тождество: (xy)b Иллюстрации:
y |
|
|
|
6 |
|
|
|
|
|
=2 |
|
|
|
|
=1 |
|
|
|
|
|
|
=1=2 |
|
1 |
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
- |
|
1 |
|
|
0 |
|
x |
|
Рис. 1. ( > 0)
|
lim |
b = 0; |
lim xb = + |
1 |
; (b > |
||
x |
! |
0+0 x |
x |
! |
1 |
|
|
|
+ |
|
|
||||
= xb yb (b – произвольно).
y
6
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=2 |
- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
||
Рис. 2. ( < 0)
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
|
sh x = ex e x – гиперболический синус, |
|
||||||||
|
|
|
|
2 |
|
|
|
|
||
|
ch x = ex+e x – гиперболический косинус, |
|
||||||||
|
th x = sh x |
2 |
exx e xx |
|
– гиперболический тангенс, |
|
||||
|
= |
|
|
|||||||
|
|
ch x |
|
e +e |
|
|
|
|||
|
ch x |
|
ex+e x |
|
|
|
||||
cth x = sh x |
= |
|
(x 6= 0) – гиперболический котангенс. |
|
||||||
ex e x |
|
|||||||||
Из |
непрерывности |
показательной |
функции |
и |
||||||
арифметических свойств непрерывных функций следует непрерывность гиперболических функций: sh x (x 2
R); ch x (x 2 R); th x (x 2 R); cth x (x 2 R; x 6= 0).
63

Эскизы графиков гиперболических функций:
y6 |
|
y6 |
|
ch x |
sh x |
|
|
|
|
|
|
|
|
|
cth x |
1 |
- |
1 |
th x- |
0 |
x |
0 |
x |
|
|
1 |
|
|
|
cth x |
|
Замечание. Для гиперболических функций имеют место формулы, аналогичные формулам для тригонометрических
функций. Например, ch2 x sh2 x = 1; 2 ch x sh x = sh 2x; sh(x y) = sh x ch y ch x sh y и т. д.
64
