2.3. Вращательное движение твердого тела.

Движение твердого тела может быть поступательным и вращательным. При поступательном движении твердого тела все его элементарные объемы имеют одинаковую скорость и описывают в пространстве одинаковые траектории, смещенные друг относительно друга.

При вращательном движении вокруг некоторой оси элементарные объемы твердого тела описывают окружности в плоскостях, перпендикулярных оси вращения. Каждый элементарный объем движется со скоростью

г де - скорость движения элементарного объема вдоль траектории, - угловая скорость его движения, , -угол поворота тела за время , - кратчайшее расстояние от оси вращения до рассматриваемого элементарного объема тела (см. рис. 2.2).

Угловая скорость - векторная величина. Направление угловой скорости определяется правилом буравчика.

Покажем, что любое движение твердого тела может быть представлено в виде поступательного и вращательного движений. Для этого рассмотрим два положения произвольно движущегося тела (см. рис. 2.3) - положение А и положение Б. В положении А на теле произвольным образом выберем точку О, обозначим эту точку на теле в положении Б и произведем поступательное перемещение тела из положения А в положение Б так, чтобы точки О совпали. Потом повернем тело вокруг точки О на некоторый угол , так, чтобы совпали все остальные точки тела.

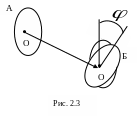
Можно показать, что от выбора точки О угол поворота не зависит. Изменение угла во времени определяет угловую скорость. Из сказанного следует, что угловая скорость для любого элементарного объема, принадлежащего вращающемуся твердому телу, одинакова.

Так как каждый из векторов и в Декартовой системе координат имеет три компоненты, то для полного описания движения любой точки твердого тела нужно знать шесть независимых величин: , где и угловые скорости вращения вокруг осей и соответственно. Поэтому говорят, что твердое тело имеет шесть степеней свободы движения.

2.4. Момент инерции

Определим кинетическую энергию тела, совершающего вращательное движение. Для поступательного движения дело обстоит просто: т.к. все точки тела движутся с одинаковой скоростью , то кинетическая энергия будет определяться выражением , где масса всего тела.

Определим теперь кинетическую энергию вращательного движения. Для этого, мысленно разделим тело на элементарные объемы и будем считать их материальными точками. Если масса -го элемента, а - кратчайшее расстояние этого элемента до оси вращения, то модуль его скорости будет равна , где - угловая скорость вращения тела. Кинетическая энергия этого элемента тела будет равна

.

Очевидно, полная кинетическая энергия вращения твердого тела определяется суммой кинетических энергий всех составляющих тело элементов, т.е.

,

где и зависит только от распределения массы тела относительно оси предполагаемого вращения. Эта величина называется моментом инерции. Как мы увидим в дальнейшем, момент инерции характеризует инерционные свойства тела способного вращаться и является аналогом массы при вращательном движении.

В общем случае, момент инерции находится интегрированием:

Пределы интегрирования определяются распределением массы тела относительно оси предполагаемого вращения, зависимостью от .

Рассмотрим некоторые частные случаи.

1. Вычислим момент инерции однородного длинного тонкого стержня (длина стержня , его масса ), ось предполагаемого вращения которого перпендикулярна его оси симметрии и проходит через его центр инерции.

Очевидно, масса стержня , где - плотность материала тела, - объем тела, - радиус стержня. Единственной переменной величиной зависящей от расстояния до оси вращения является длина, поэтому выражение для имеет вид: , где - та переменная, по которой производится интегрирование. Пределы интегрирования определяются положением оси предполагаемого вращения. В данном случае , а . Поэтому:

Итак, для рассмотренного случая, .

2. Вычислим момент инерции однородного длинного стержня (длина стержня , его масса ), ось предполагаемого вращения которого перпендикулярна оси симметрии и проходит через его край (см. рис. 2.5).

Очевидно, что для решения этой задачи можно воспользоваться предыдущей, изменив только пределы интегрирования - . Вследствие этого имеем:

.

.

2. Вычислим момент инерции однородного сплошного диска (радиус диска , его масса ), ось предполагаемого вращения которого проходит через его центр инерции и перпендикулярна его торцевой поверхности (см. рис. 2.6).

Масса диска , где -плотность материала, из которого изготовлен диск, - его объем, - толщина диска. Единственной переменной величиной, зависящей от расстояния до оси вращения, является радиус, поэтому выражение для имеет вид: , где - та переменная, по которой производится интегрирование. Пределы интегрирования определяются расположением оси предполагаемого вращения. В данном случае , а . Поэтому:

Итак, для рассмотренного случая имеем:

.

2. Вычислим момент инерции однородного диска с центральным отверстием (внешний радиус - , радиус отверстия , масса - ), ось предполагаемого вращения которого проходит через его центр инерции и перпендикулярна его торцевой поверхности.

Как и ранее, для решения этой задачи воспользуемся предыдущей, изменив только пределы интегрирования - . Таким образом, имеем:

,

или, с учетом того, что масса диска с отверстием равна

.

2. Момент инерции однородного шара массой и радиуса определяется выражением:

.