Дослідження функції на екстремум за допомогою похідних вищих порядків.

Нехай у точці х = х₁ f (x₁) = 0 і f (x₁) існує й неперервна в деякому околі точки х₁.

Теорема. Якщо f(x₁) = 0, то функція f(x) у точці х = х₁ має максимум, якщо f (x₁) < 0 і мінімум, якщо f (x₁) > 0.

Доведення.

Нехай f (x₁) = 0 і f (x₁) < 0. Оскільки функція f(x) неперервна, то f (x₁) буде від’ємною й у деякій малому околі точки х₁.

Оскільки f (x) = (f (x)) < 0, то f (x) спадає на відрізку, що містить точку х₁, але f (x₁)=0, тобто f (x) > 0 при х<x₁ і f (x) < 0 при x > x₁. Це й означає, що при переході через точку х = х₁ похідна f (x) міняє знак з “+” на “–“, тобто в цій точці функція f(x) має максимум.

Для випадку мінімуму функції теорема доводиться аналогічно.

Якщо f(x) = 0, то характер критичної точки невідомий. Для його визначення потрібне подальше дослідження.

Опуклість і увігнутість кривої. Точки перегину.

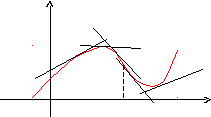
Визначення. Крива звернена опуклістю догори на інтервалі (а, b), якщо всі її точки лежать нижче будь-якої її дотичної на цьому інтервалі. Крива, звернена опуклістю нагору, називається опуклою, а крива, звернена опуклістю вниз – називається увігнутою.

у

x

На малюнку показана ілюстрація наведеного вище визначення.

Теорема 1. Якщо у всіх точках інтервалу (a, b) друга похідна функції f(x) від’ємна, то крива y = f(x) звернена опуклістю нагору (опукла).

Доведення. Нехай х₀  (a, b). Проведемо дотичну до кривої в цій точці.

Рівняння кривої: y = f(x);

Рівняння дотичної:

Слід довести, що .

За теоремою Лагранжа для f(x) – f(x₀): , x₀ < c < x.

За теоремою Лагранжа для .

Нехай х > x₀ тоді x₀ < c₁ < c < x. Оскільки x – x₀ > 0 і c – x₀ > 0, і крім того за умовою

, отже, .

Нехай x < x₀ тоді x < c < c₁ < x₀ і x – x₀ < 0, c – x₀ < 0, оскільки за умовою тому .

Аналогічно доводиться, що якщо f (x) > 0 на інтервалі (a, b), то крива y = f(x) увігнута на інтервалі (a, b).

Теорему доведено.

Визначення. Точка, що відокремлює опуклу частину кривої від увігнутої, називається точкою перегину.

Очевидно, що в точці перегину дотична перетинає криву.

Теорема 2. Нехай крива визначається рівнянням y = f(x). Якщо друга похідна f(a) = 0 або f(a) не існує й при переході через точку х = а f(x) міняє знак, то точка кривої з абсцисою х = а є точкою перегину.

Доведення. 1) Нехай f (x) < 0 при х < a і f (x) > 0 при x > a. Тоді при x < a крива опукла, а при x > a крива увігнута, тобто точка х = а – точка перегину.

2) Нехай f (x) > 0 при x < b і f (x) < 0 при x < b. Тоді при x < b крива звернена опуклістю вниз, а при x > b – опуклістю нагору. Тоді x = b – точка перегину.

Теорему доведено.