Властивості еволюти.

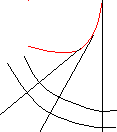
Теорема 1: Нормаль до даної кривої є дотичною до її еволюти.

Теорема 2: Модуль різниці радіусів кривизни в будь-яких точках кривої дорівнює модулю довжини відповідної еволюти.

C₃

C₂

C₁

R₁ R₂ R₃

M₁

M’₁ M₂ M₃

M’₂

M’₃

Треба відзначити, що будь-якій еволюті відповідає нескінченне число евольвент.

Зазначені вище властивості можна проілюструвати в такий спосіб: якщо на еволюту натягнута нитка, то евольвента є траєкторною лінією кінця нитки при її змотуванні або розмотуванні за умови, що нитка перебуває в натягнутому стані.

Приклад: Знайти рівняння еволюти кривою, заданої рівняннями:

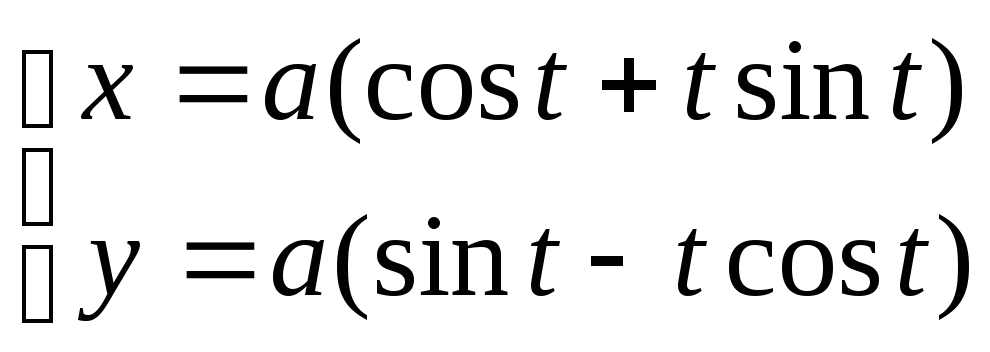
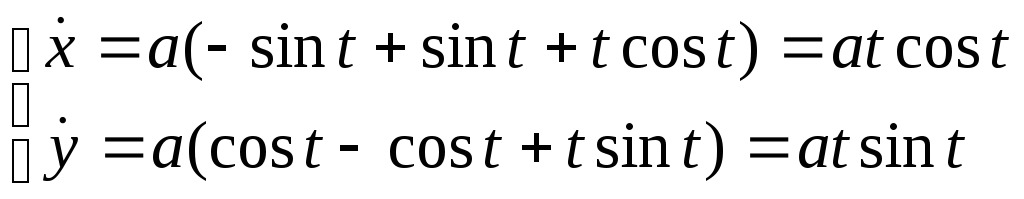
Рівняння еволюти:

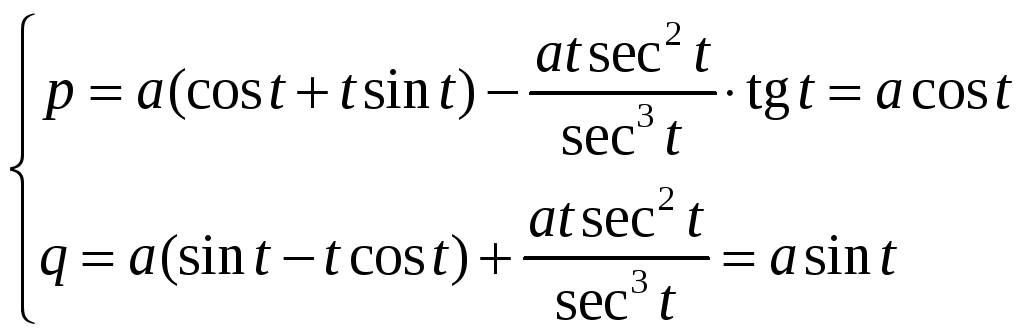
Остаточно: 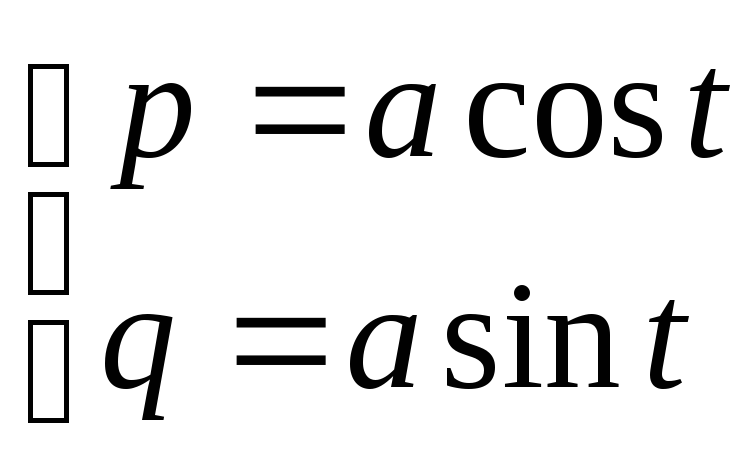– це рівняння кола із центром на початку координат радіуса а.

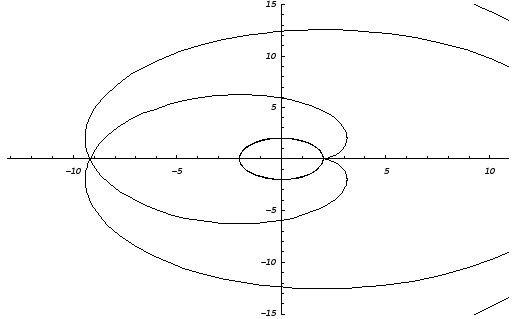
Вихідна крива виходить свого роду розгорненням кола.

Нижче наведені графіки вихідної кривої і її еволюти.

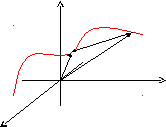
Кривизна просторової кривої.

z

A(x, y, z)

B

O y

x

Для довільної точки А, що перебуває на просторовій кривій, координати можуть бути визначені як функції деякої довжини дуги S.

x =  (S); y =  (S); z = f (S);

Наведене вище рівняння називають векторним рівнянням лінії в просторі.

Визначення: Лінія, що опише в просторі змінний радіус-вектор при зміні параметра S, називається годографом цього вектора.

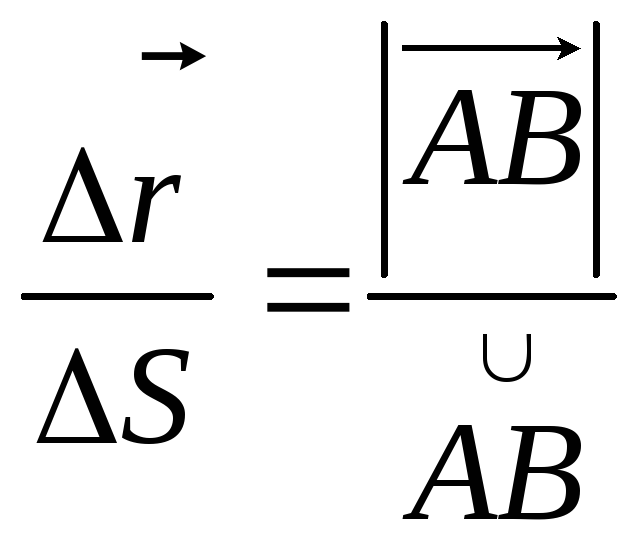, тоді – вектор, спрямований по дотичній до кривої в точці А(x, y, z).

Але оскільки , то – одиничний вектор, спрямований по дотичній.

Якщо прийняти , то .

Причому .

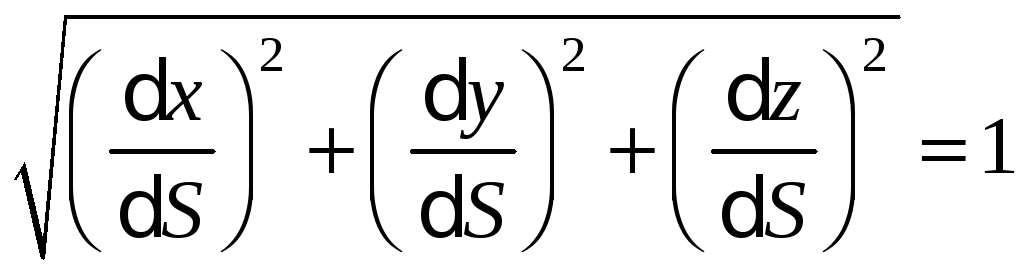Розглянемо другу похідну

Визначення: Пряма з напрямком, що співпадає з напрямком вектора називається головною нормаллю до кривої. Її одиничний вектор позначається .

, де K – кривизна кривої.

Кривизна просторової кривої може бути знайдена за формулою:

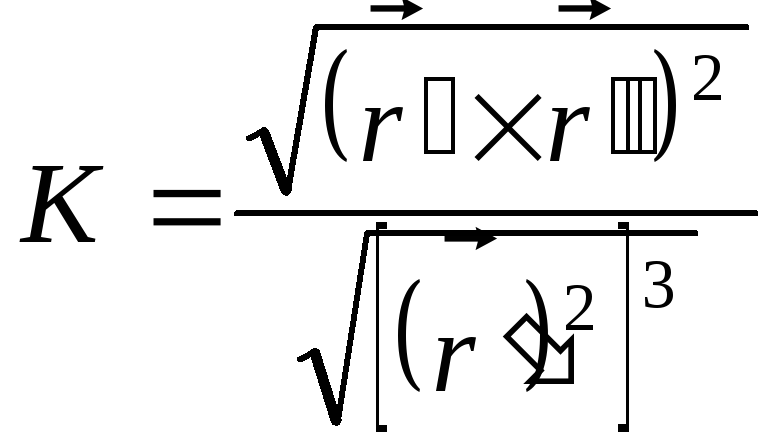
Можливий й інший запис формули для кривизни просторової кривої (вона виходить із наведеної вище формули):

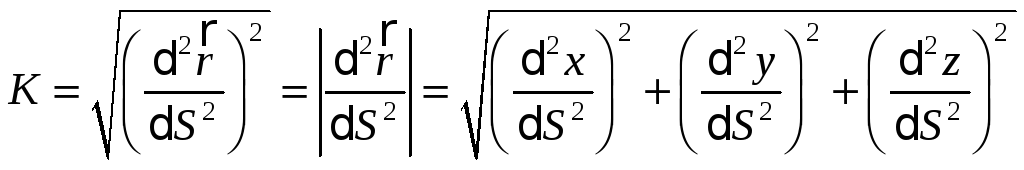
Визначення: Вектор називається вектором кривизни. Величина називається радіусом кривизни.

Про формули Френе.

Формулами Френе називаються співвідношення:

Остання формула отримана із двох перших.

У цих формулах:

– одиничний вектор головної нормалі до кривої,

– одиничний вектор бінормалі,

R – радіус кривизни кривої ,

Т – радіус кручення кривої.

Визначення: Площина, що проходить через дотичну й головну нормаль до кривої в точці А називається дотичною площиною.

Визначення: Нормаль до кривої, перпендикулярна до дотичної площини, називається бінормаллю. Її одиничний вектор – .

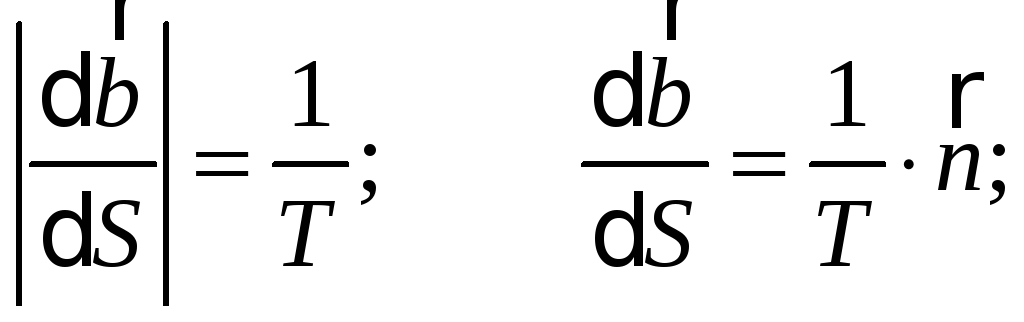
Величина називається крученням кривої.

Нижче розглянемо кілька прикладів дослідження методами диференціального числення різних типів функцій.

Приклад: Методами диференціального числення дослідити функцію й побудувати її графік.

1. Областю визначення даної функції є всі дійсні числа (-; ).

2. Функція є функцією загального виду в сенсі парності й непарності.

3. точки перетину з координатними осями: з віссю Оу: x = 0; y = 1;

з віссю Ох: y = 0; x = 1;

4. Точки розриву й асимптоти: Вертикальних асимптот немає.

Похилі асимптоти: загальне рівняння y = kx + b;

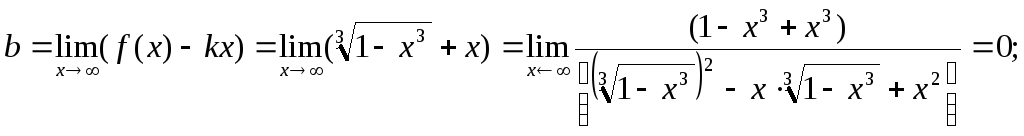
Отже: y = – х – похила асимптота.

5. Зростання й спадання функції, точки екстремуму.

. Видно, що y 0 при будь-якому х  0, отже, функція спадає на всій області визначення й не має екстремумів. У точці х = 0 перша похідна функції дорівнює нулю, однак у цій точці спадання не змінюється на зростання, отже, у точці х = 0 функція швидше за все має перегин. Для знаходження точок перегину, знаходимо другу похідну функції.

; y = 0 при х =0 і y =  при х = 1.

Точки (0,1) і (1,0) є точками перегину, тому що y(1 – h) < 0; y(1 + h) >0; y(– h) > 0; y(h) < 0 для будь-якого h > 0.

6. Побудуємо графік функції.

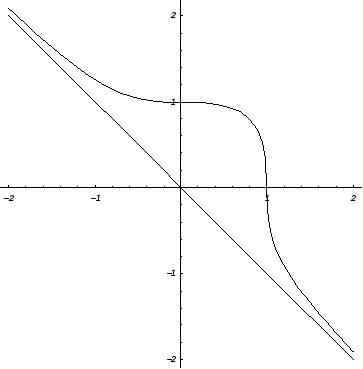
Приклад: Дослідити функцію й побудувати її графік.

1. Областю визначення функції є всі значення х, крім х = 0.

2. Функція є функцією загального виду в сенсі парності й непарності.

3. Точки перетину з координатними осями: c віссю Ох: y = 0; x =

с віссю Оу: x = 0; y – не існує.

4. Точка х = 0 є точкою розриву , отже, пряма х = 0 є вертикальної асимптотою.

Похилі асимптоти шукаємо у вигляді: y = kx + b.

Похила асимптот y = х.

5. Знаходимо точки екстремуму функції.

; y = 0 при х = 2, y =  при х = 0.

y > 0 при х  (– , 0) – функція зростає,

y < 0 при х  (0, 2) – функція спадає,

у > 0 при х  (2, ) – функція зростає.

Таким чином, точка (2, 3) є точкою мінімуму.

Для визначення характеру опуклості/увігнутості функції знаходимо другу похідну.

> 0 при будь-якому х  0, отже, функція увігнута на всій області визначення.

6. Побудуємо графік функції.

Приклад: Досліджувати функцію й побудувати її графік.

1. Областю визначення даної функції є проміжок х  (– , ).

2. У сенсі парності й непарності функція є функцією загального виду.

3. Точки перетину з осями координат: з віссю Оу: x = 0, y = 0;

з віссю Ох: y = 0, x = 0, x = 1.

4. Асимптоти кривої.

Вертикальних асимптот немає.

Спробуємо знайти похилі асимптоти у вигляді y = kx + b.

– похилих асимптот не існує.

5. Знаходимо точки екстремуму.

Для знаходження критичних точок слід розв’язати рівняння 4х³ – 9х² +6х –1 = 0.

Для цього розкладемо даний багаточлен третього ступеня на множники.

Підбором можна визначити, що одним з коренів цього рівняння є число х = 1. Тоді:

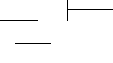4x³ – 9x² + 6x – 1 x – 1

4x³ – 4x² 4x² – 5x + 1

– 5x² + 6x

– 5x² + 5x

x – 1

x – 1

0

Тоді можна записати (х – 1)(4х² – 5х + 1) = 0. Остаточно одержуємо дві критичні точки: x = 1 і x = 1/4.

Примітка. Операції ділення багаточленів можна було уникнути, якщо при знаходженні похідної скористатися формулою похідної добутку:

Знайдемо другу похідну функції: 12x² – 18x + 6. Прирівнюючи до нуля, знаходимо:

x = 1, x = 1/2.

Систематизуємо отриману інформацію в таблиці:

	(–  ; ¼)	1/4	( ¼ ; ½)	1/2	( ½ ; 1)	1	(1 ; )
f(x)	+	+	+	0	–	0	+
f(x)	–	0	+	+	+	0	+
f(x)	спадає увігнута	min	зростає увігнута	перегин	зростає опукла	перегин	зростає опукла

6. Побудуємо графік функції.