Застосування диференціала до наближених обчислень.

Диференціал функції y = f(x) залежить від х і є головною частиною приросту х.

Також можна скористатися формулою

Тоді абсолютна похибка

Відносна похибка

Більш докладне застосування диференціала до наближених обчислень буде описано нижче.

Теореми про середнє. Теорема Ролля.

(Ролль (1652–1719) – французький математик)

Якщо функція f(x) неперервна на відрізку [a, b], диференційована на інтервалі (а, b) і значення функції на кінцях відрізка рівні f(a) = f(b), то на інтервалі (а, b) існує точка , a <  < b, у якій похідна функція f(x) рівна нулю, f() = 0.

Геометричний зміст теореми Ролля полягає в тому, що при виконанні умов теореми на інтервалі (a, b) існує точка  така, що у відповідній точці кривої y = f(x) дотична паралельна осі Ох. Таких точок на інтервалі може бути й трохи, але теорема затверджує існування принаймні однієї такої точки.

Доведення. По властивості функцій, неперервних на відрізку функція f(x) на відрізку [a, b] приймає найбільше й найменше значення. Позначимо ці значення М і m відповідно. Можливі два різних випадки М = m і M  m.

Нехай M = m. Тоді функція f(x) на відрізку [a, b] зберігає постійне значення й у будь-якій точці інтервалу її похідна дорівнює нулю. У цьому випадку за  можна прийняти будь-яку точку інтервалу.

Нехай М = m. Тоді значення на кінцях відрізка рівні, то хоча б одне зі значень М або m функція приймає усередині відрізка [a, b]. Позначимо , a <  < b точку, у якій f() = M. Тому що М – найбільше значення функції, то для кожного х ( будемо вважати, що точка  + х перебуває усередині розглянутого інтервалу) вірна нерівність:

При цьому

Але тому що за умовою похідна в точці  існує, то існує й границя .

Оскільки 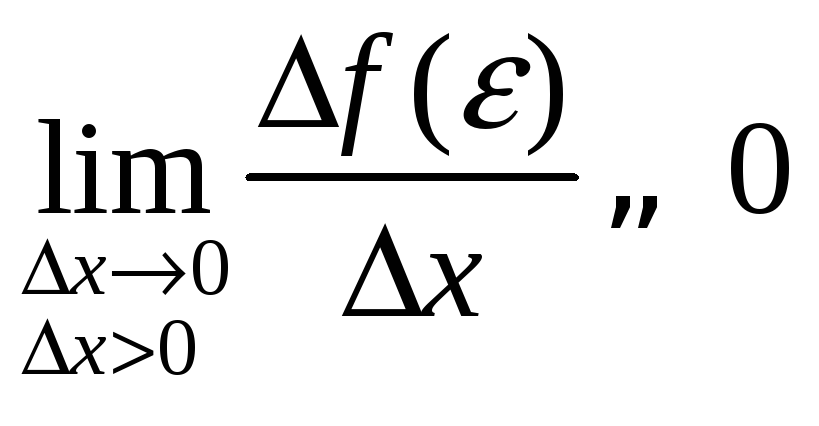і 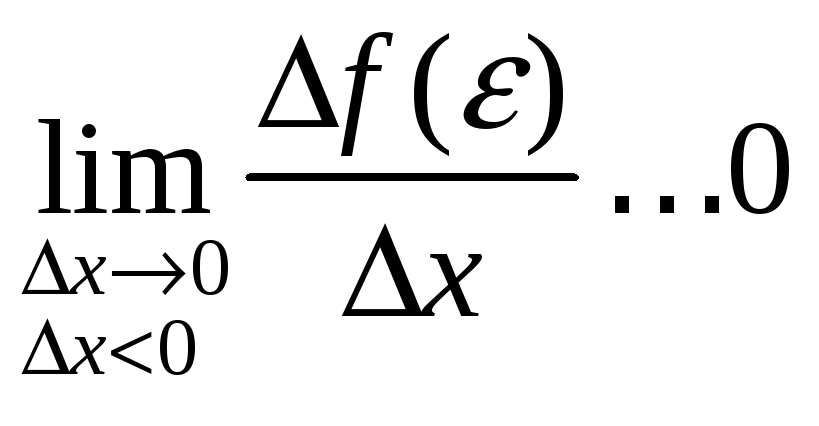, то можна зробити висновок:

Теорему доведено.

Теорема Ролля має кілька наслідків:

1. Якщо функція f(x) на відрізку [a, b] задовольняє теоремі Ролля, причому f(a) = f(b) = = 0, то існує принаймні одна точка , a <  < b, така, що f () = 0. Тобто між двома нулями функції знайдеться хоча б одна точка, у якій похідна функції дорівнює нулю.

2. Якщо на розглянутому інтервалі (а, b) функція f(x) має похідну (n–1)-го порядку й n раз обертається в нуль, то існує принаймні одна точка інтервалу, у якій похідна (n – 1)-го порядку дорівнює нулю.

Теорема Лагранжа.

(Жозеф Луї Лагранж (1736–1813) французький математик)

Якщо функція f(x) неперервна на відрізку [a, b] і диференційована на інтервалі (а, b), то на цьому інтервалі найдеться принаймні одна точка  a <  < b, така, що .

Це означає, що якщо на деякому проміжку виконуються умови теореми, то відношення приросту функції до приросту аргументу на цьому відрізку дорівнює значенню похідної у деякій проміжній точці.

Розглянута вище теорема Ролля є частковим випадком теореми Лагранжа.

Відношення дорівнює кутовому коефіцієнту січної АВ.

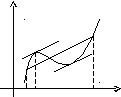у

В

А

0 а  b x

Якщо функція f(x) задовольняє умовам теореми, то на інтервалі (а, b) існує точка  така, що у відповідній точці кривої y = f(x) дотична паралельна січній, що з'єднує точки А і В. Таких точок може бути й трохи, але одна існує точно.

Доведення. Розглянемо деяку допоміжну функцію

F(x) = f(x) – y_{сек АВ}

Рівняння січної АВ можна записати у вигляді:

Функція F(x) задовольняє теоремі Ролля. Дійсно, вона неперервна на відрізку [a, b] і диференційована на інтервалі (а, b). За теоремою Ролля існує хоча б одна точка , a <  < b, така що F() = 0.

Оскільки , то , отже

Теорему доведено.

Визначення. Вираз називається формулою Лагранжа або формулою скінчених приростів.

Надалі ця формула буде дуже часто застосовуватися для доведення найрізноманітніших теорем.

Іноді формулу Лагранжа записують у трохи іншому вигляді:

,

де 0 <  < 1, x = b – a, y = f(b) – f(a).