Заміна змінних у подвійному інтегралі.
Розглянемо
подвійний інтеграл виду
,
де змінна
х змінюється
в границях від a
до b,
а змінна y
– від 1(x)
до 2(х).
Покладемо х = f(u, v); y = (u, v)
Тоді
dx
=
;
dy
=
;
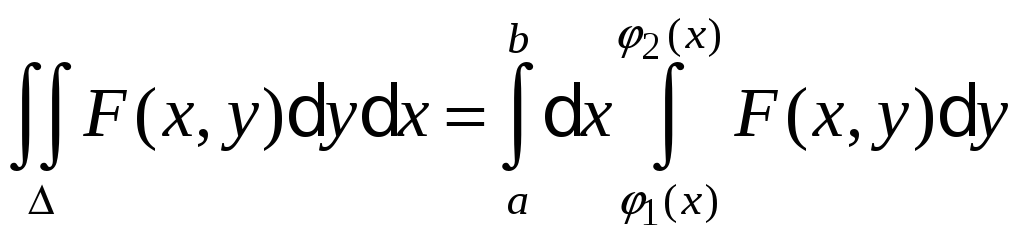
оскільки при першому інтегруванні змінна х приймається за сталу, то dx = 0.
,
тобто
підставляючи цей вираз в записане вище співвідношення для dy, одержуємо:
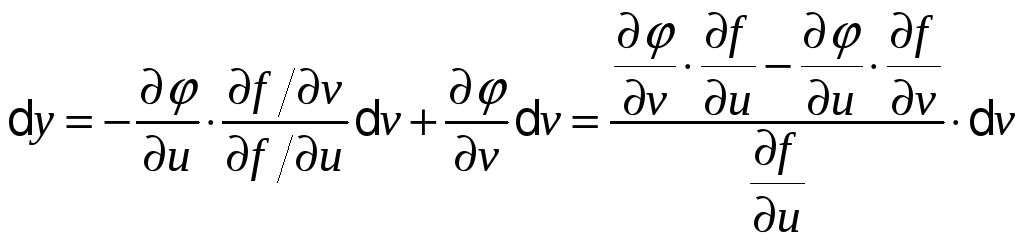
Вираз
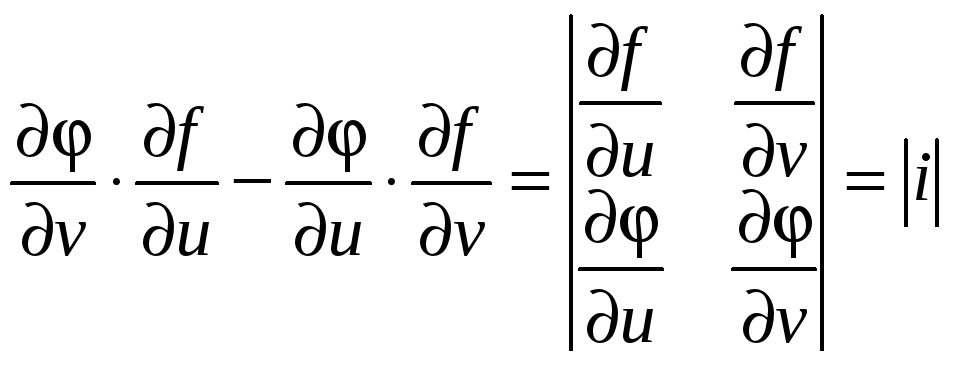називається визначником
Якобі або
Якобіаном
функцій
f(u,
v)
і (u,
v).
(Якобі Карл Густав Якоб – (1804–1851) – німецький математик)
Тоді
Оскільки
при першому інтегруванні наведений
вище вираз для dx
приймає вигляд
(
при першому інтегруванні думаємо v
= const, dv
= 0), то при зміні порядку інтегрування,
одержуємо співвідношення:
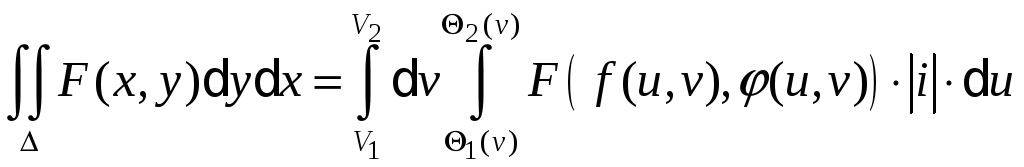
Подвійний інтеграл у полярних координатах.
Скористаємося формулою заміни змінних:
При
цьому відомо, що
У цьому випадку Якобіан має вигляд:
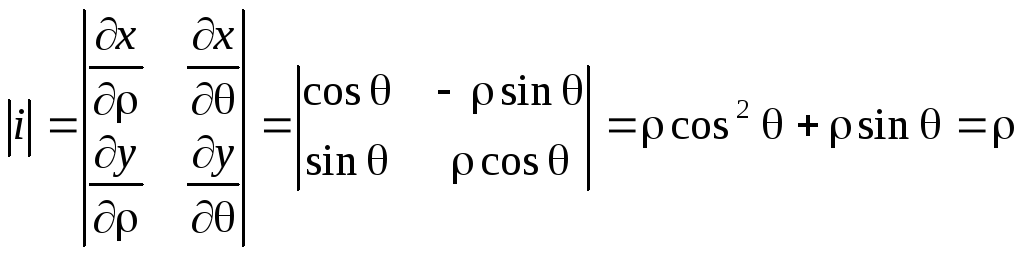
Тоді
Тут
– нова область значень,
Потрійний інтеграл.
При розгляді потрійного інтеграла не будемо докладно зупинятися на всіх тих теоретичних викладках, які були детально розібрані стосовно до подвійного інтеграла, тому що істотних розходжень між ними немає.
Єдина відмінність полягає в тому, що при знаходженні потрійного інтеграла інтегрування ведеться не по двох, а по трьох змінних, а областю інтегрування є не частина площини, а деяка область у тривимірному просторі.
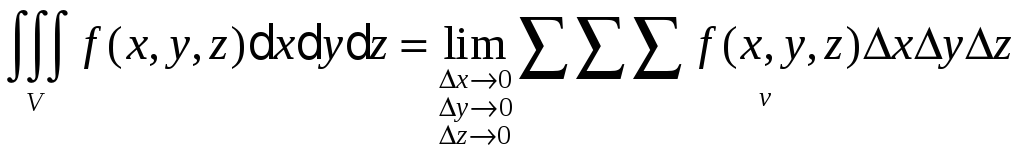
Підсумовування проводиться по області V, що обмежена деякою поверхнею (x, y, z) = 0.
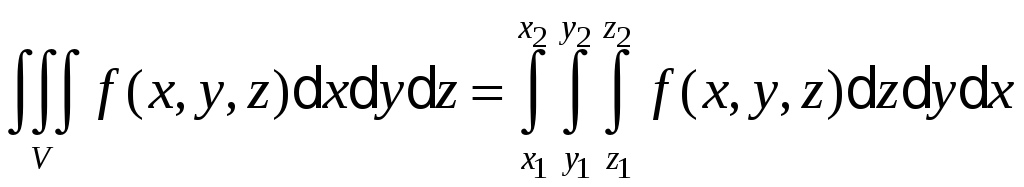
Тут х1 і х2 – сталу величини, y1 і y2 – можуть бути деякими функціями від х або постійними величинами, z1 і z2 – можуть бути функціями від х та y або сталими величинами.
Приклад.
Обчислити інтеграл
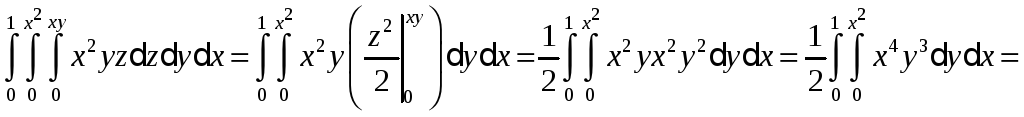
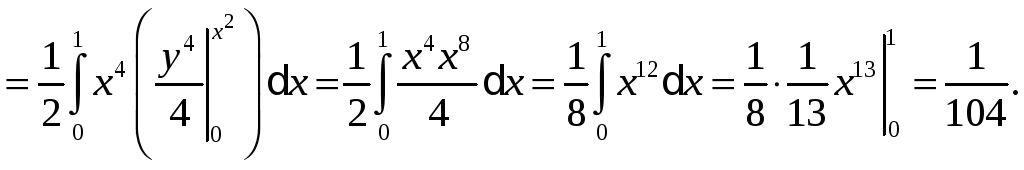
Заміна змінних у потрійному інтегралі.
Операція заміни змінних у потрійному інтегралі аналогічна відповідній операції для подвійного інтеграла.
Можна записати:
Найчастіше до заміни змінної в потрійному інтегралі вдаються з метою перейти від декартовій прямокутної системи координат до циліндричної або сферичної системи. Див. Циліндрична та сферична системи координат.
Розглянемо ці перетворення докладніше.
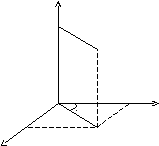
Циліндрична система координат.
z
P
z
0
x
y
Зв'язок координат довільної точки Р простору в циліндричній системі з координатами в декартовій прямокутній системі здійснюється за формулами:
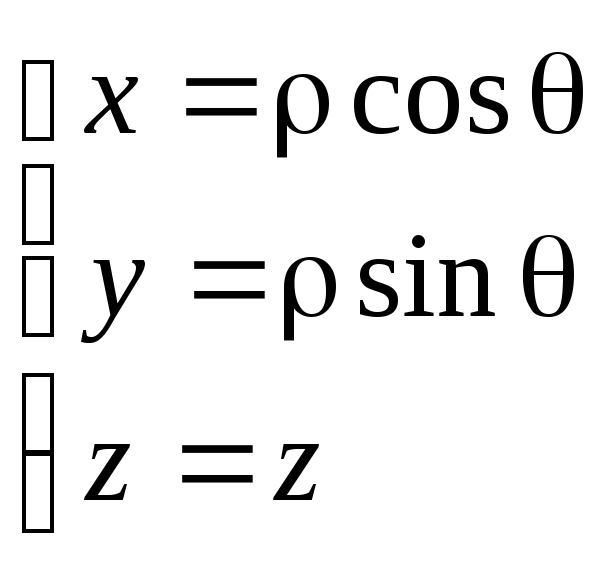
Для подання потрійного інтеграла в циліндричних координатах обчислюємо Якобіан:
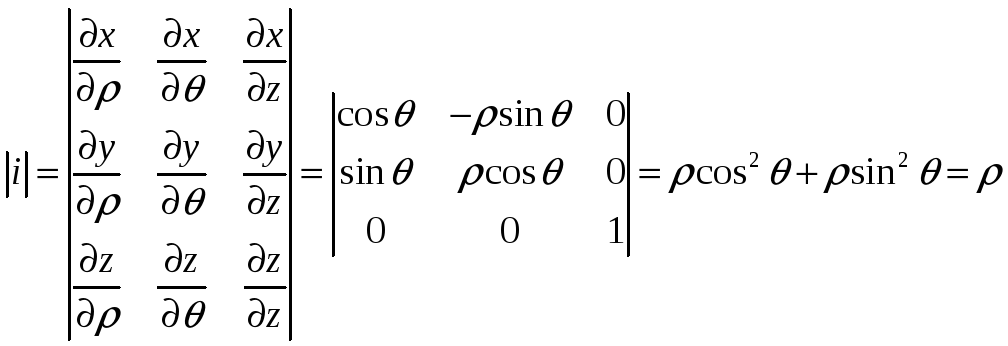
Разом:
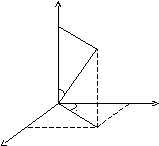
Сферична система координат.
z
P
0 x
y
Зв'язок координат довільної точки Р простору в сферичній системі з координатами в декартовій прямокутній системі здійснюється за формулами:
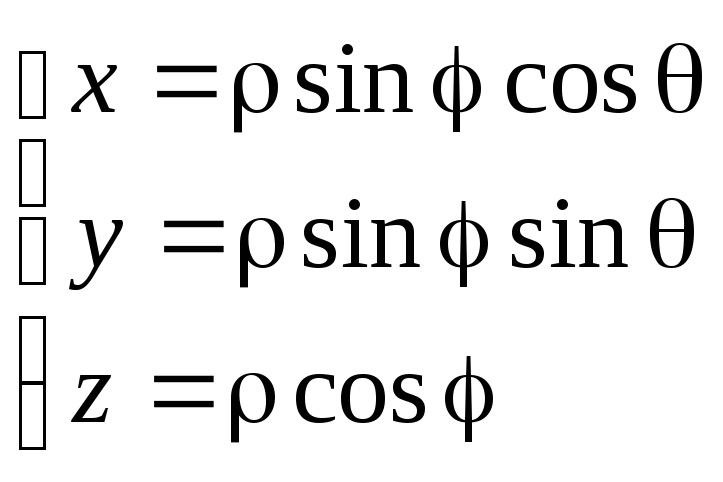
Для подання потрійного інтеграла в сферичних координатах обчислюємо Якобіан:
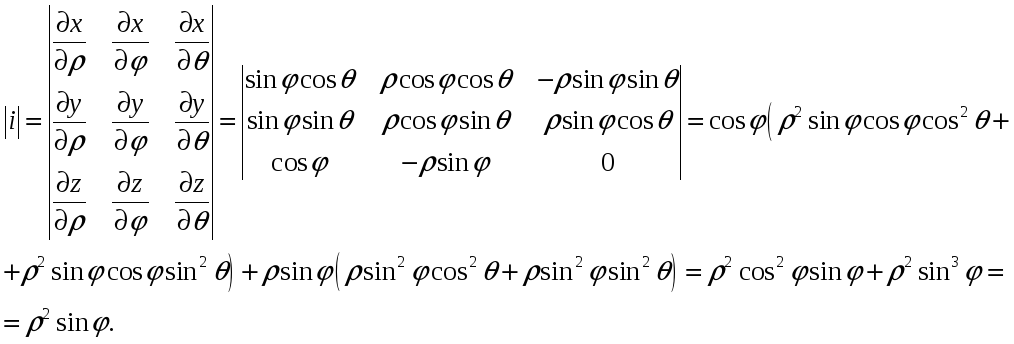
Остаточно одержуємо:
