Теорема Коші.

(Коші (1789–1857) – французький математик)

Якщо функції f(x) і g(x) неперервні на відрізку [a, b] і диференційовані на інтервалі (a, b) і g(x)  0 на інтервалі (a, b), то існує принаймні одна точка , a <  < b, така, що

.

Тобто відношення приростів функцій на даному відрізку дорівнює відношенню похідних у точці .

Для доведення цієї теореми на перший погляд дуже зручно скористатися теоремою Лагранжа. Записати формулу скінченних різниць для кожної функції, а потім розділити їхній одну на одну. Однак, це враження помилкове, тому що точка  для кожної з функцій в загальному випадку різна. Звичайно, у деяких окремих випадках ця точка інтервалу може виявитися однаковою для обох функцій, але це – дуже рідкий збіг, а не правило, тому не може бути використаний для доведення теореми.

Доведення. Розглянемо допоміжну функцію

,

яка на інтервалі [a, b] задовольняє умовам теореми Ролля. Легко бачити, що при х = а й х = b F(a) = F(b) = 0. Тоді за теоремою Ролля існує така точка , a <  < b, така, що F() = 0. Оскільки

, то

А оскільки , то

Теорему доведено.

Слід зазначити, що розглянута вище теорема Лагранжа є частковим випадком (при g(x) = x) теореми Коші. Доведена нами теорема Коші дуже широко використається для розкриття так званих невизначеностей. Застосування отриманих результатів дозволяє істотно спростити процес обчислення границь функцій, що буде докладно розглянуто нижче.

Розкриття невизначеностей. Правило Лопіталя.

(Лопіталь (1661–1704) – французький математик)

До розряду невизначеностей прийнято відносити наступні співвідношення:

Теорема (правило Лопіталя). Якщо функції f(x) і g(x) диференційовані поблизу точки а, неперервні в точці а, g(x) відмінна від нуля поблизу а й f(a) = g(a) = 0, то границя частки функцій при дорівнює границі частки їхніх похідних, якщо ця границя (скінченна або нескінченна) існує.

Доведення. Застосувавши формулу Коші, одержимо:

де  – точка, що перебуває між а й х. З огляду на що f(a) = g(a) = 0:

Нехай при ха відношення прямує до деякої границі. Оскільки точка  лежить між точками а й х, то при х  а одержимо   а, а отже й відношення прямує до того ж границі. Таким чином, можна записати:

.

Теорему доведено.

Приклад: Знайти границю .

Як видно, при спробі безпосереднього обчислення границі виходить невизначеність виду . Функції, що входять у чисельник і знаменник дробу задовольняють вимогам теореми Лопіталя.

f(x) = 2x + ; g(x) = e^x;

;

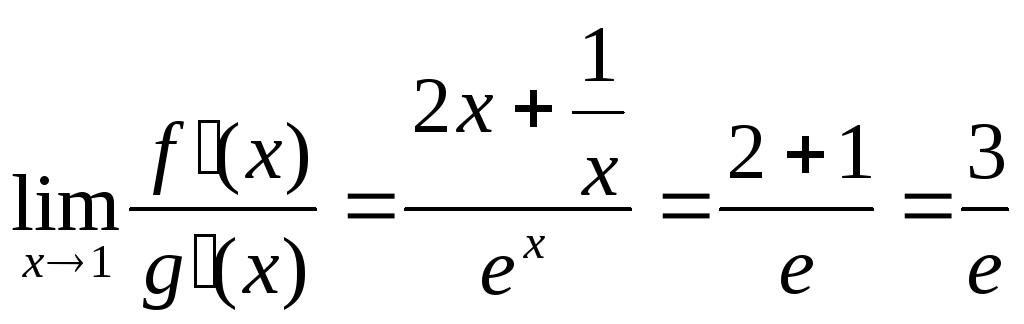Приклад: Знайти границю .

; ;

.

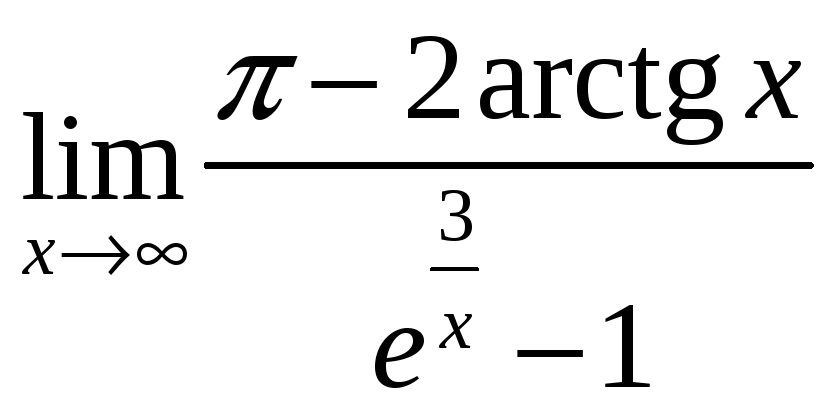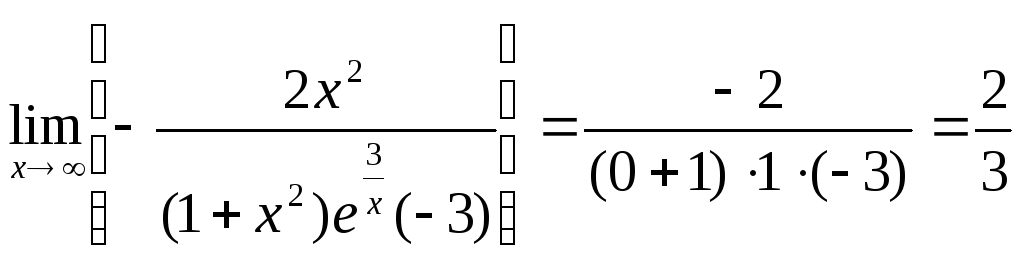Якщо при розв’язанні приклада після застосування правила Лопіталя спроба обчислити границю знову приводить до невизначеності, то правило Лопіталя може бути застосовано другий раз, третій і т.д. поки не буде отриманий результат. Природно, це можливо тільки в тому випадку, якщо знову отримані функції у свою чергу задовольняють вимогам теореми Лопіталя.

Приклад: Знайти границю .

; ;

; ;

; ;

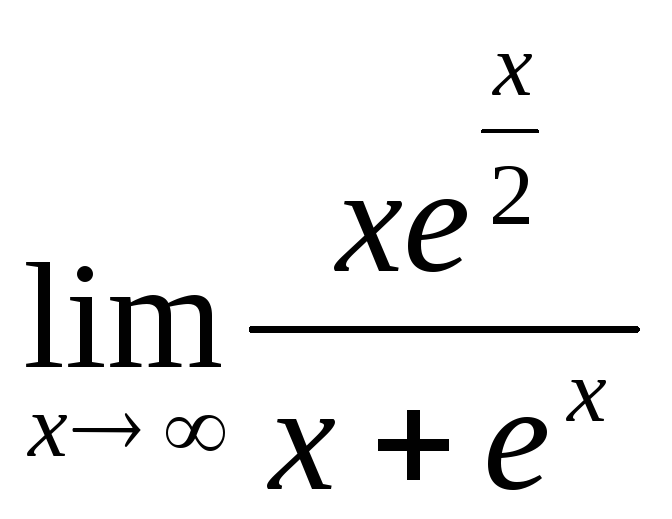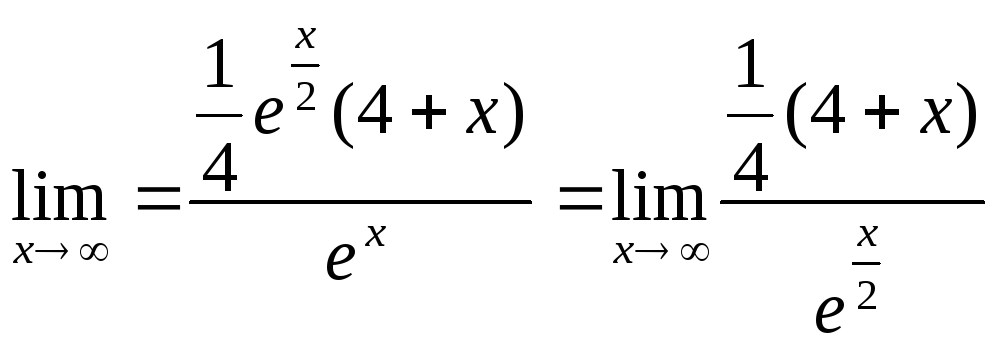
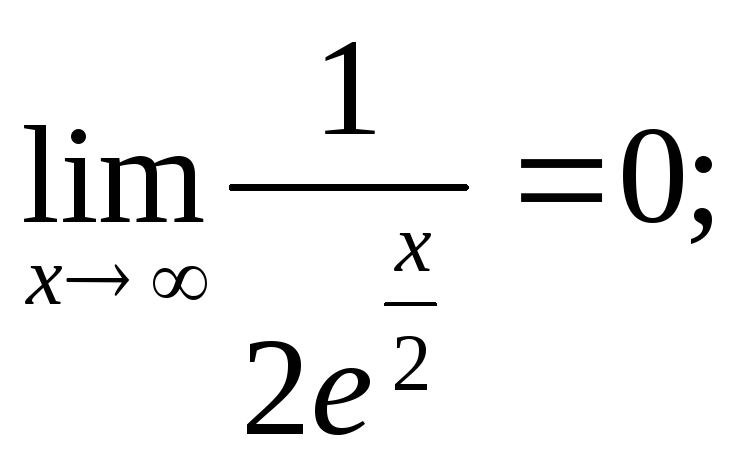
Слід зазначити, що правило Лопіталя – всього лише один зі способів обчислення границь. Часто в конкретному прикладі поряд із правилом Лопіталя може бути використаний і якийсь інший метод (заміна змінних, домноження та ін.).

Приклад: Знайти границю .

; ;

– знову вийшла невизначеність. Застосуємо правило Лопіталя ще раз.

; ;

– застосовуємо правило Лопіталя ще раз.

; ;

;

Невизначеності вигляду можна розкрити за допомогою логарифмування. Такі невизначеності зустрічаються при знаходженні меж функцій вигляду , f(x)>0 поблизу точки а при ха. Для знаходження границі такої функції досить знайти границю функції ln y = g(x) ln f(x).

Приклад: Знайти границю .

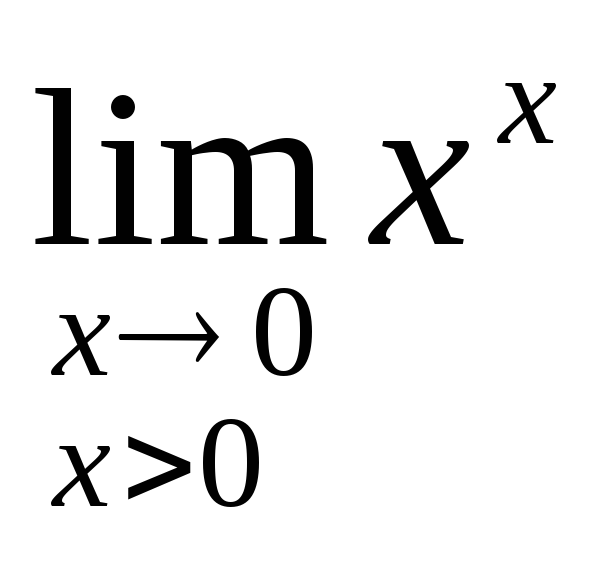Тут y = x^x, ln y = x ln x.

Тоді 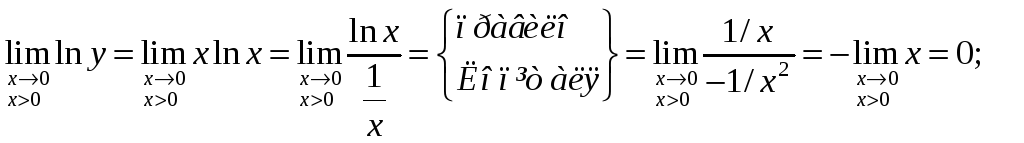. Отже

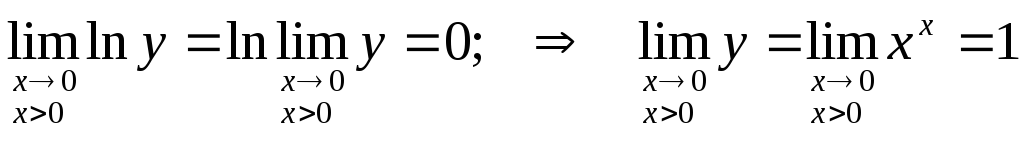
Приклад: Знайти границю .

; – одержали невизначеність. Застосовуємо правило Лопіталя ще раз.

; ;

Похідні й диференціали вищих порядків.

Нехай функція f(x) – диференційована на деякому інтервалі. Тоді, диференціюючи її, одержуємо першу похідну

Якщо знайти похідну функції f(x), одержимо другу похідну функції f(x).

тобто y = (y) або .

Цей процес можна продовжити й далі, знаходячи похідні ступеня n.

.

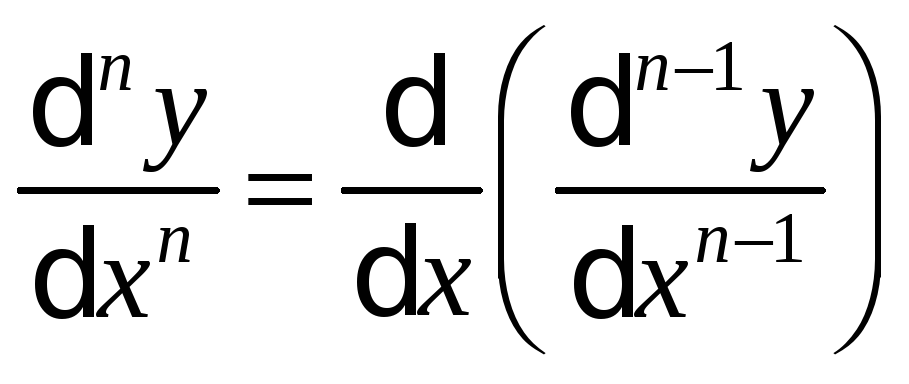Загальні правила знаходження вищих похідних.

Якщо функції u = f(x) і v = g(x) диференційовані, то

1. (Сu)⁽ⁿ⁾ = Cu⁽ⁿ⁾;

2. (u  v)⁽ⁿ⁾ = u⁽ⁿ⁾  v⁽ⁿ⁾;

3)

.

Цей вираз називається формулою Лейбніца.

Також за формулою dⁿy = f⁽ⁿ⁾(x)dxⁿ може бути знайдений диференціал n-го порядку.

Дослідження функцій за допомогою похідної.

Зростання й спадання функцій.

Теорема. 1) Якщо функція f(x) має похідну на відрізку [a, b] і зростає на цьому відрізку, то її похідна на цьому відрізку ненегативна, тобто .

2) Якщо функція f(x) неперервна на відрізку [a, b] і диференційована на проміжку (а, b), причому f(x) > 0 для a < x < b, то ця функція зростає на відрізку [a, b].

Доведення.

1. Якщо функція f(x) зростає, то f(x + x) > f(x) при x >0 і f(x + x) < f(x) при x<0,

тоді:

2) Нехай f(x)>0 для будь-яких точок х₁ і х₂, що належать відрізку [a, b], причому x₁<x₂.

Тоді за теоремою Лагранжа: f(x₂) – f(x₁) = f()(x₂ – x₁), x₁ <  < x₂

За умовою f()>0, отже, f(x₂) – f(x₁) >0, тобто функція f(x) зростає.

Теорему доведено.

Аналогічно можна зробити висновок про те, що якщо функція f(x) спадає на відрізку [a, b], то на цьому відрізку. Якщо у проміжку (a, b), то f(x) спадає на відрізку [a, b].

Звичайно, дане твердження справедливо, якщо функція f(x) неперервна на відрізку [a, b] і диференційована на інтервалі (a, b).

Доведену вище теорему можна проілюструвати геометрично:

y y

   

x x