Наближені обчислення за допомогою повного диференціала.

Нехай функція f(x, y) диференційована в точці (х, у). Знайдемо повний приріст цієї функції:

Якщо підставити в цю формулу вираз

то одержимо наближену формулу:

Приклад. Обчислити приблизно значення , виходячи зі значення функції при x = 1, y = 2, z = 1.

Із заданого виразу визначимо x = 1,04 – 1 = 0,04, y = 1,99 – 2 = – 0,01,

z = 1,02 – 1 = 0,02.

Знайдемо значення функції u(x, y, z) =

Знаходимо частинні похідні:

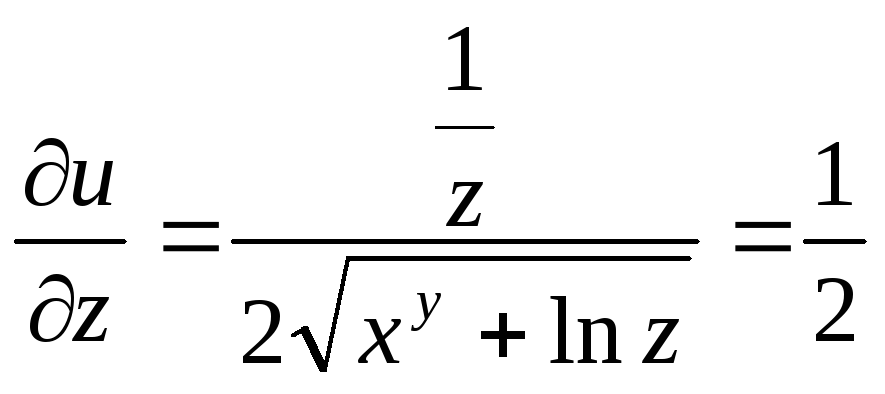
Повний диференціал функції u дорівнює:

Точне значення цього виразу: 1,049275225687319176.

Частинні похідні вищих порядків.

Якщо функція f (x, y) визначена в деякій області D, то її частки похідні й теж будуть визначені в тій же області або її частині.

Будемо називати ці похідні частинними похідними першого порядку.

Похідні цих функцій будуть частинними похідними другого порядку.

Продовжуючи диференціювати отримані рівності, одержимо частинні похідні вищих порядків.

Визначення. Частинні похідні виду і далі називаються змішаними похідними.

Теорема. Якщо функція f(x, y) і її частинні похідні визначені й неперервні в точці М(х, у) і її околі, то вірне співвідношення:

.

Тобто частинні похідні вищих порядків не залежать від порядку диференціювання.

Аналогічно визначаються диференціали вищих порядків.

…………………

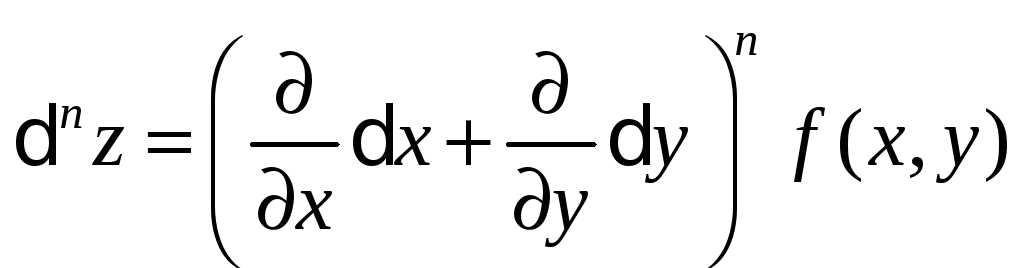
Тут n – символічний ступінь похідної, на яку заміняється реальний ступінь після піднесення до нього виразу в дужках.

Екстремум функції декількох змінних.

Визначення. Якщо для функції z = f(x, y), визначеної в деякій області, у деякому околі точки М₀(х₀, y₀) вірна нерівність

то точка М₀ називається точкою максимуму.

Визначення. Якщо для функції z = f(x, y), визначеної в деякій області, у деякому околі точки М₀(х₀, y₀) вірна нерівність

то точка М₀ називається точкою мінімуму.

Теорема. (Необхідні умови екстремуму).

Якщо функція f (x, y) у точці (х₀, y₀) має екстремум, то в цій точці або обидві її частинні похідні першого порядку дорівнюють нулю , або хоча б одна з них не існує.

Цю точку (х₀, y₀) будемо називати критичною точкою.

Теорема. (Достатні умови екстремуму).

Нехай в околі критичної точки (х₀, y₀) функція f(x, y) має неперервні частинні похідні до другого порядку включно. Розглянемо вираз:

1. Якщо D (x₀, y₀) > 0, то в точці (х₀, y₀) функція f (x, y) має екстремум, якщо – максимум, якщо 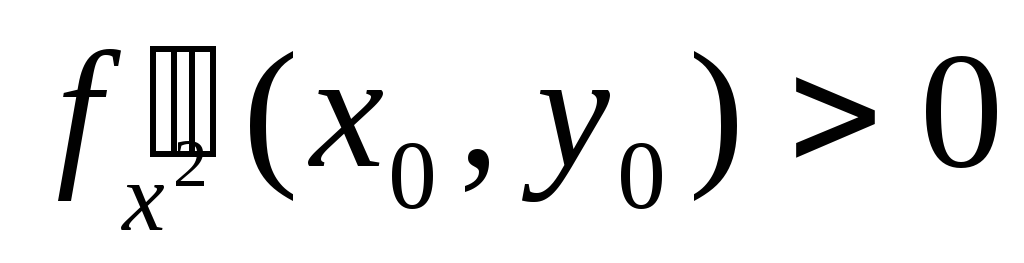– мінімум.

2. Якщо D (x₀, y₀) < 0, то в точці (х₀, y₀) функція f (x, y) не має екстремуму. У випадку, якщо D = 0, висновок про наявність екстремуму зробити не можна.

Умовний екстремум.

Умовний екстремум знаходиться, коли змінні x і y, що входять у функцію u = f (x, y), не є незалежними, тобто існує деяке співвідношення (х, у) = 0, що називається рівнянням зв'язку.

Тоді зі змінних х і y тільки одна буде незалежною, тому що інша може бути виражена через неї з рівняння зв'язку.

Тоді u = f (x, y(x)).

У точках екстремуму:

(1)

Крім того:

(2)

Помножимо рівність (2) на число  і складемо з рівністю (1).

Для виконання цієї умови у всіх точках знайдемо невизначений коефіцієнт  так, щоб виконувалася система трьох рівнянь:

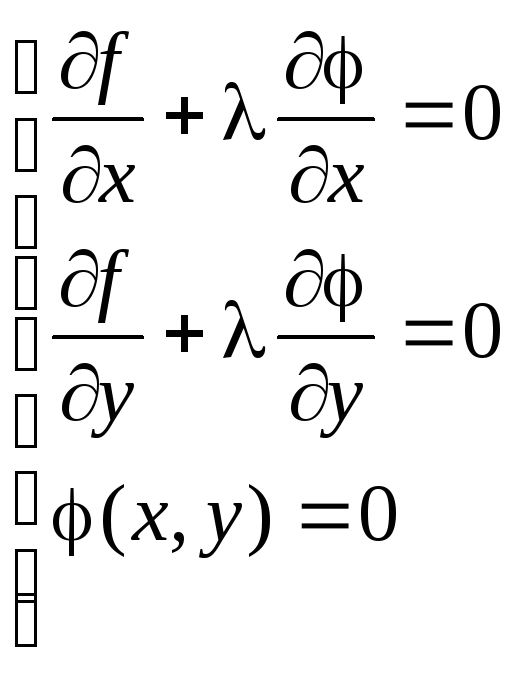
Отримана система рівнянь є необхідними умовами умовного екстремуму. Однак ця умова не є достатньою. Тому при знаходженні критичних точок потрібно їхнє додаткове дослідження на екстремум.

Вираз u = f (x, y) + (x, y) називається функцією Лагранжа.

Приклад. Знайти екстремум функції f (x, y) = xy, якщо рівняння зв'язку:

2x + 3y – 5 = 0

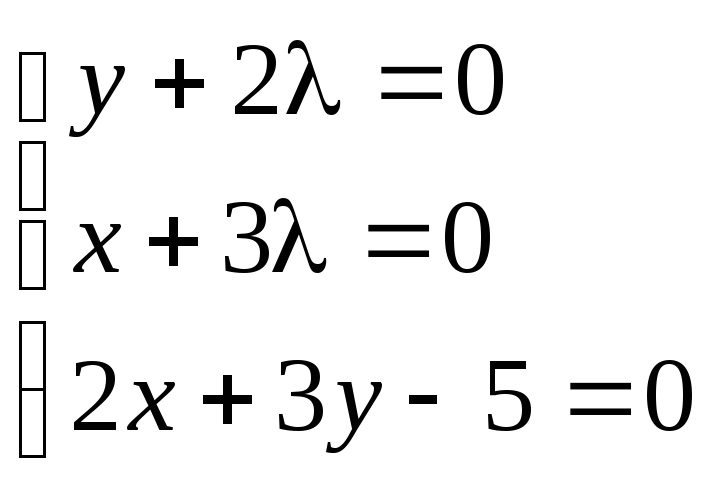
Таким чином, функція має екстремум у точці .

Використання функції Лагранжа для знаходження точок екстремуму функції називається також методом множників Лагранжа.

Вище ми розглянули функцію двох змінних, однак, всі міркування щодо умовного екстремуму можуть бути поширені на функції більшого числа змінних.