Формула Тейлора.

Тейлор (1685–1731) – англійський математик

Теорема Тейлора. 1) Нехай функція f(x) має в точці х = а й деякому її околі похідні порядку до (n+1) включно. {Тобто і всі попередні до порядку n функції і їхні похідні неперервні й диференційовані в цьому околі}.

2) Нехай х – будь-яке значення з цього околу, але х  а.

Тоді між точками х і а знайдеться така точка , що справедливо формула:

– цей вираз називається формулою Тейлора, а вираз:

називається залишковим членом у формі Лагранжа.

Доведення. Представимо функцію f(x) у вигляді деякого багаточлена P_n(x), значення якого в точці х = а дорівнює значенню функції f(x), а значення його похідних дорівнює значенням відповідних похідних функції в точці х = а.

(1)

Багаточлен P_n(x) буде близький до функції f(x). Чим більше значення n, тим ближче значення багаточлена до значень функції, тим точніше він повторює функцію.

Представимо цей багаточлен з невизначеними поки коефіцієнтами:

(2)

Для знаходження невизначених коефіцієнтів обчислюємо похідні багаточлена в точці х = а й становимо систему рівнянь:

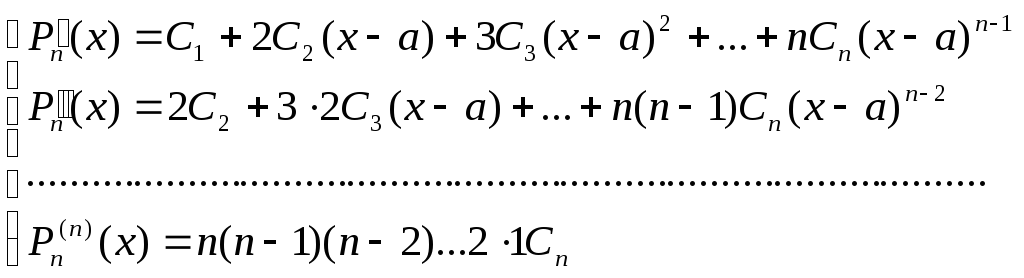(3)

Розв’язки цієї системи при х = а не викликає утруднень, одержуємо:

……………………......

Підставляючи отримані значення C_i у формулу (2), одержуємо:

Як було помічено вище, багаточлен не точно збігається з функцією f(x), тобто відрізняється від неї на деяку величину. Позначимо цю величину R_n+1(x). Тоді:

f(x) = P_n(x) + R_n+1(x)

Теорему доведено.

Р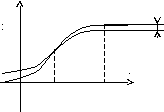озглянемо докладніше величину R_n+1(x).

y

f(x) R_n+1(x)

P_n(x)

0 a x x

Як видно на малюнку, в точці х = а значення багаточлена в точності співпадає зі значенням функції. Однак, при видаленні від точки х = а розбіжність значно збільшується.

Іноді використається інший запис для R_n+1(x). Оскільки точка  (a, x), то найдеться таке число  з інтервалу 0 <  < 1, що  = a + (x – a).

Тоді можна записати:

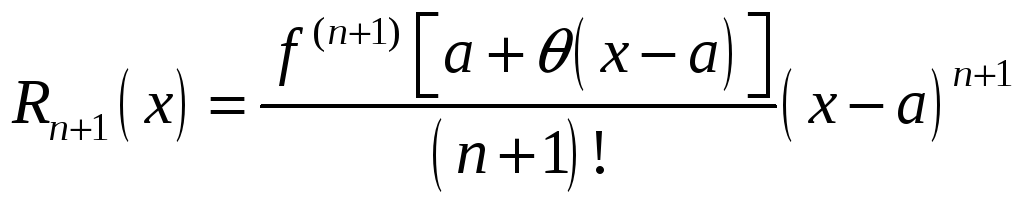
Тоді, якщо прийняти a = x₀, x – a = x, x = x₀ + x, формулу Тейлора можна записати у вигляді:

де 0 <  < 1.

Якщо прийняти n = 0, одержимо: f(x₀ + x) – f(x₀) = f(x₀ + x)x – це вираз називається формулою Лагранжа. (Жозеф Луї Лагранж (1736–1813) французький математик і механік).

Формула Тейлора має величезне значення для різних математичних перетворень. З її допомогою можна знаходити значення різних функцій, інтегрувати, вирішувати диференціальні рівняння та інше.

При розгляді степеневих рядів буде більш докладно описані деякі особливості й умови розкладу функції за формулою Тейлора.

Формула Маклорена.

Колін Маклорен (1698–1746) шотландський математик.

Формулою Маклорена називається формула Тейлора при а = 0:

Ми одержали так звану формулу Маклорена із залишковим членом у формі Лагранжа.

Слід зазначити, що при розкладі функції в ряд, застосування формули Маклорена краще, ніж застосування безпосередньо формули Тейлора, тому що обчислення значень похідних у нулі простіше, ніж у будь-якій іншій точці, природно, за умови, що ці похідні існують.

Однак, вибір числа а дуже важливий для практичного використання. Справа в тому, що при обчисленні значення функції в точці, розташованої відносно близько до точки а, значення, отримане за формулою Тейлора, навіть при обмеженні трьома – чотирма першими доданками, збігається з точним значенням функції практично абсолютно. При видаленні ж розглянутої точки від точки а для одержання точного значення треба брати все більшу кількість доданків формули Тейлора, що незручно.

Тобто чим більше по модулі значення різниці (х – а) тим більше точне значення функції відрізняється від знайденого за формулою Тейлора.

Крім того, можна показати, що залишковий член R_n+1(x) є нескінченно малою функцією при ха, причому більш високого порядку, ніж (х – а)ⁿ, тобто

.

Таким чином, ряд Маклорена можна вважати частковим випадком ряду Тейлора.