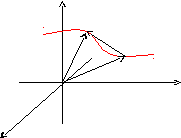
Векторна функція скалярного аргументу.

z

A(x, y, z)

y

х

Нехай деяка крива в просторі заданий параметрично:

x =  (t); y =  (t); z = f(t);

Радіус-вектор довільної точки кривої: .

Таким чином, радіус-вектор точки кривої може розглядатися як деяка векторна функція скалярного аргументу t. При зміні параметра t змінюється величина і напрямок вектора .

Запишемо співвідношення для деякої точки t₀:

Тоді вектор – границя функції (t). .

Очевидно, що

, тоді

.

Щоб знайти похідну векторної функції скалярного аргументу, розглянемо приріст радіус-вектора при деякому прирості параметра t.

; ;

або, якщо існують похідні  (t),  (t), f (t), то

Цей вираз – вектор похідна вектора .

Якщо є рівняння кривої:

x =  (t); y =  (t); z = f(t);

то в довільній точці кривої А(x_А, y_А, z_А) з радіус-вектором

можна провести пряму з рівнянням

Оскільки похідна – вектор, спрямований по дотичній до кривої, то

.

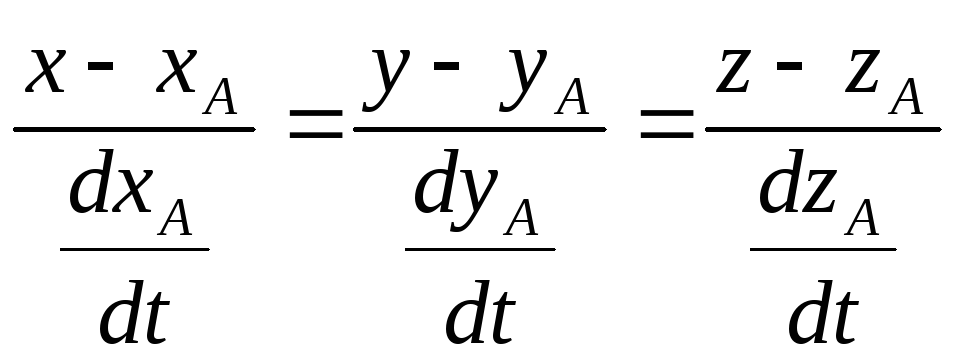Властивості похідної векторної функції скалярного аргументу.

1)

2) , де  = (t) – скалярна функція

3)

4)

Рівняння нормальної площини до кривої буде мати вигляд:

Приклад. Скласти рівняння дотичної і нормальної площини до лінії, заданої рівнянням у точці t = /2.

Рівняння, що описують криву, по осях координат мають вигляд:

x(t) = cos t; y(t) = sin t; z(t) = ;

Знаходимо значення функцій і їхніх похідних у заданій точці:

x(t) = – sin t; y(t) = cos t;

x(/2) = –1; y(/2) = 0; z(/2) =

x(/2) = 0; y(/2) = 1; z(/2) = /2

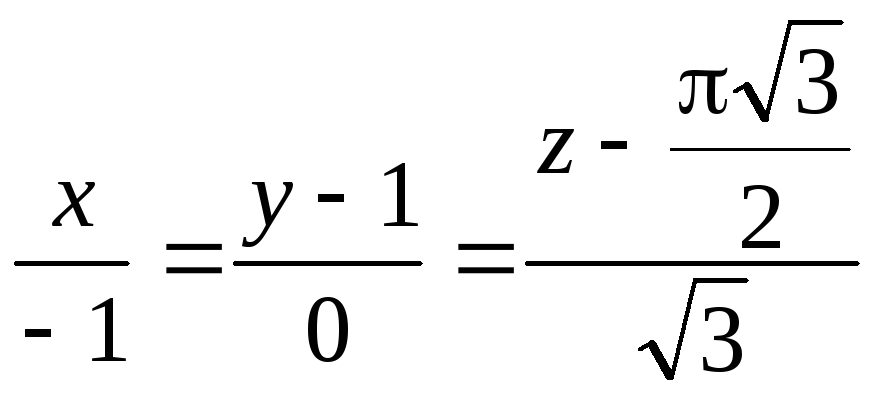– це рівняння дотичної.

Нормальна площина має рівняння:

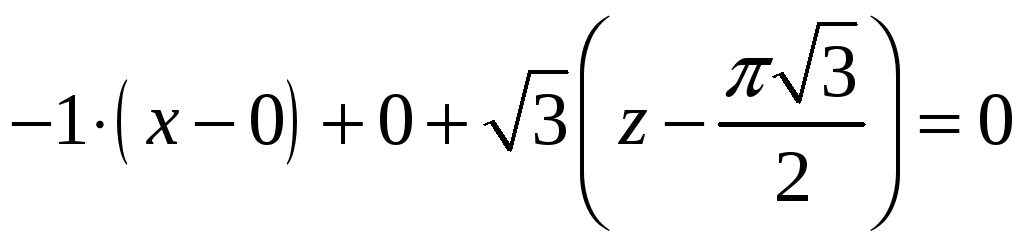
Параметричне задання функції.

Дослідження й побудова графіка кривої, що задана системою рівнянь вигляду:

,

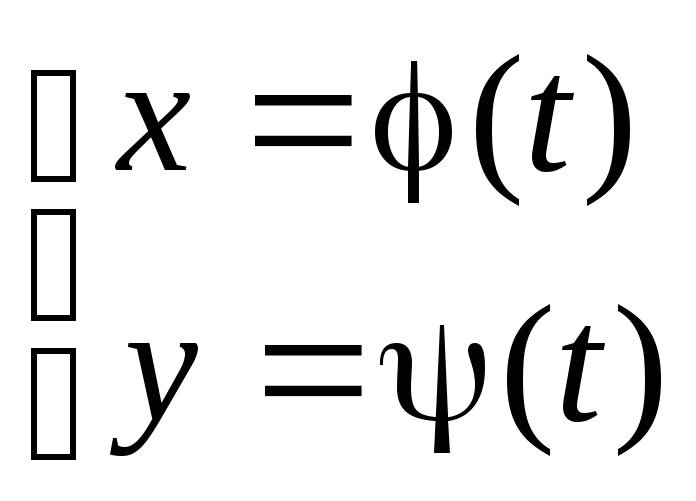проводиться загалом аналогічно дослідженню функції вигляду y = f(x).

Знаходимо похідні:

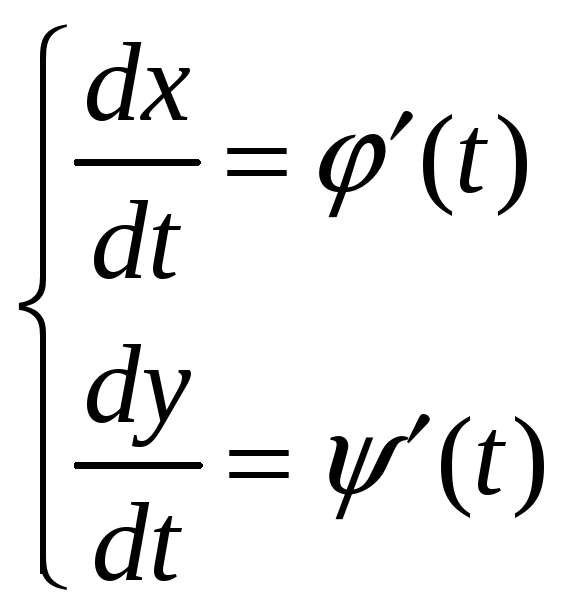
Тепер можна знайти похідну . Далі знаходяться значення параметра t, при яких хоча б одна з похідних (t) або (t) дорівнює нулю або не існує. Такі значення параметра t називаються критичними.

Для кожного інтервалу (t₁, t₂), (t₂, t₃), … , (t_k-1, t_k) знаходимо відповідний інтервал (x₁, x₂), (x₂, x₃), … , (x_k-1, x_k) і визначаємо знак похідної на кожному з отриманих інтервалів, тим самим визначаючи проміжки зростання й спадання функції.

Далі знаходимо другу похідну функції на кожному з інтервалів і, визначаючи її знак, знаходимо напрямок опуклості кривої у кожній точці.

Для знаходження асимптот знаходимо такі значення t, при наближенні до яких або х або y прямує до нескінченності, і такі значення t, при наближенні до яких і х і y прямують до нескінченності.

В іншому дослідження проводиться аналогічно тому, як і дослідження функції, заданої безпосередньо.

На практиці дослідження параметрично заданих функцій здійснюється, наприклад, при знаходженні траєкторії об'єкта, що рухається, де роль параметра t виконує час.

Нижче розглянемо докладніше деякі широко відомі типи параметрично заданих кривих.