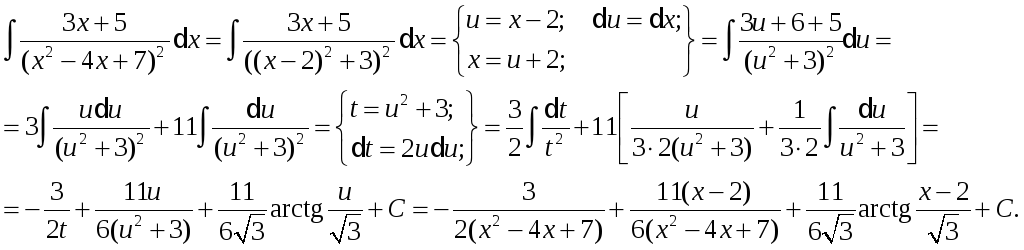- •Диференціальне числення функції однієї змінної. Похідна функції, її геометричний і фізичний зміст.
- •Однобічні похідні функції в точці.
- •Похідна показниково-степеневої функції.
- •Похідна оберненої функцій.
- •Диференціал функції.
- •Формула Тейлора.
- •Формула Маклорена.
- •Подання деяких елементарних функцій за формулою Тейлора.
- •Застосування диференціала до наближених обчислень.
- •Теореми про середнє. Теорема Ролля.
- •Теорема Лагранжа.
- •Теорема Коші.
- •Розкриття невизначеностей. Правило Лопіталя.
- •Точки екстремуму.
- •Дослідження функції на екстремум за допомогою похідних вищих порядків.
- •Опуклість і увігнутість кривої. Точки перегину.
- •Асимптоти.
- •Вертикальні асимптоти.
- •Похилі асимптоти.
- •Векторна функція скалярного аргументу.
- •Властивості похідної векторної функції скалярного аргументу.
- •Параметричне задання функції.
- •Рівняння деяких типів кривих у параметричній формі. Коло.
- •Циклоїда.
- •Астроїда.
- •Похідна функції, заданої параметрично.
- •Кривизна плоскої кривої.
- •Властивості еволюти.
- •Кривизна просторової кривої.
- •Про формули Френе.
- •Інтегральне числення. Первісна функція.
- •Невизначений інтеграл.
- •Методи інтегрування.
- •Безпосереднє інтегрування.
- •Спосіб підстановки (заміни змінних).
- •Інтегрування частинами.
- •Інтегрування елементарних дробів.
- •Інтегрування раціональних функцій. Інтегрування раціональних дробів.
- •Інтегрування деяких тригонометричних функцій.
- •Інтеграл виду .
- •Інтеграл виду , якщо функція r є непарною відносно cos X.
- •Інтегрування деяких ірраціональних функцій.
- •Інтеграл виду де n – натуральне число.
- •Інтегрування біноміальних диференціалів.
- •Інтеграли виду .
- •1 Спосіб. Тригонометрична підстановка.
- •2 Спосіб. Підстановки Ейлера. (1707–1783)
- •3 Спосіб. Метод невизначених коефіцієнтів.
- •Кілька прикладів інтегралів, що не виражаються через елементарні функції.
- •Визначений інтеграл.
- •Властивості визначеного інтеграла.
- •Обчислення визначеного інтеграла.
- •Заміна змінних.
- •Інтегрування частинами.
- •Наближене обчислення визначеного інтеграла.
- •Формула прямокутників.
- •Формула трапецій.
- •Формула парабол
- •Невласні інтеграли.
- •Інтеграл від розривної функції.
- •Геометричні застосування визначеного інтеграла. Обчислення площ плоских фігур.
- •Знаходження площі криволінійного сектора.
- •Обчислення довжини дуги кривої.
- •Обчислення об'ємів тіл. Обчислення об'єму тіла за відомими площами його паралельних перетинів.
- •Об'єм тіл обертання.
- •Площа поверхні тіла обертання.
- •Функції декількох змінних
- •Похідні й диференціали функцій декількох змінних.
- •Повний приріст і повний диференціал.
- •Геометричний зміст повного диференціала. Дотична площина й нормаль до поверхні.
- •Наближені обчислення за допомогою повного диференціала.
- •Частинні похідні вищих порядків.
- •Екстремум функції декількох змінних.
- •Умовний екстремум.
- •Похідна за напрямком.
- •Градієнт.
- •Зв'язок градієнта з похідною за напрямком.
- •Кратні інтеграли.
- •Подвійні інтеграли.
- •Умови існування подвійного інтеграла.
- •Властивості подвійного інтеграла.
- •Обчислення подвійного інтеграла.
- •Заміна змінних у подвійному інтегралі.
- •Подвійний інтеграл у полярних координатах.
- •Потрійний інтеграл.
- •Заміна змінних у потрійному інтегралі.
- •Циліндрична система координат.
- •Сферична система координат.
- •Геометричні й фізичні застосування кратних інтегралів.
Спосіб підстановки (заміни змінних).
Теорема:
Якщо потрібно знайти інтеграл
![]() ,
але складно відшукати первісну, то за
допомогою заміни x
= (t)
і dx
= (t)dt
виходить:
,
але складно відшукати первісну, то за
допомогою заміни x
= (t)
і dx
= (t)dt
виходить:
![]()
Доведення: Продиференціюємо пропоновану рівність:
![]()
По розглянутому вище властивості №2 невизначені інтеграли:
f (x)dx = f [(t)](t) dt
що з урахуванням введених позначень і є вихідним припущенням. Теорему доведено.
Приклад.
Знайти невизначений інтеграл
![]() .
.
Зробимо заміну t = sin x, dt = cos x dt.
![]()
Приклад.
![]()
Заміна
![]() Одержуємо:
Одержуємо:
![]()
Нижче будуть розглянуті інші приклади застосування методу підстановки для різних типів функцій.
Інтегрування частинами.
Спосіб заснований на відомій формулі похідної добутку:
(uv) = uv + vu
де u і v – деякі функції від х.
У диференціальній формі: d(uv) = udv + vdu
Проінтегрувавши,
одержуємо:
![]() ,
а відповідно до наведених вище
властивостей невизначеного інтеграла:
,
а відповідно до наведених вище
властивостей невизначеного інтеграла:
![]() або
або ![]() ;
;
Одержали формулу інтегрування частинами, що дозволяє знаходити інтеграли багатьох елементарних функцій.
Приклад.
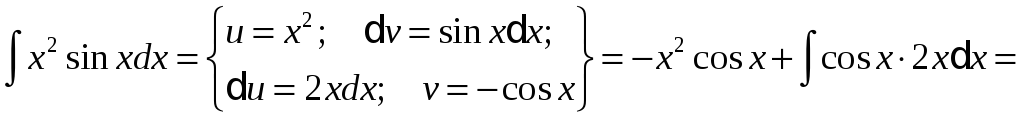
![]()
Як видно, послідовне застосування формули інтегрування частинами дозволяє поступово спростити функцію й привести інтеграл до табличного.
Приклад.
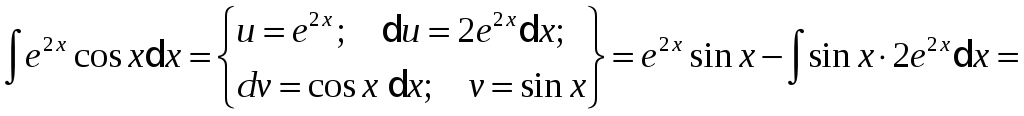
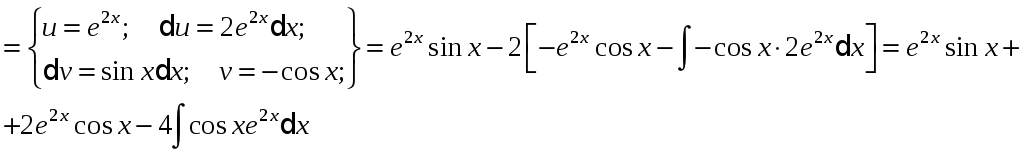
Видно, що в результаті повторного застосування інтегрування частинами функцію не вдалося спростити до табличного виду. Однак, останній отриманий інтеграл нічим не відрізняється від вихідного. Тому перенесемо його в ліву частину рівності.
![]()
![]()
Таким чином, інтеграл знайдений взагалі без застосування таблиць інтегралів.
Перш ніж розглянути докладно методи інтегрування різних класів функцій, наведемо ще кілька прикладів знаходження невизначених інтегралів приведенням їх до табличного.
Приклад.
![]()
Приклад.
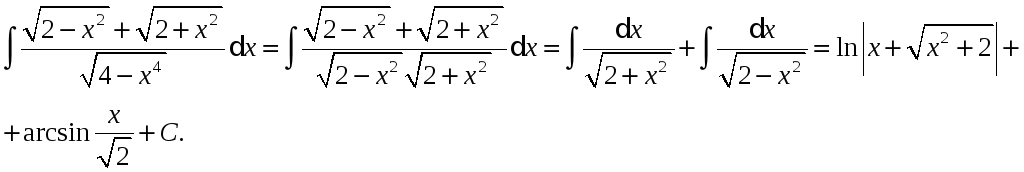
Приклад.
![]()
![]()
Приклад.
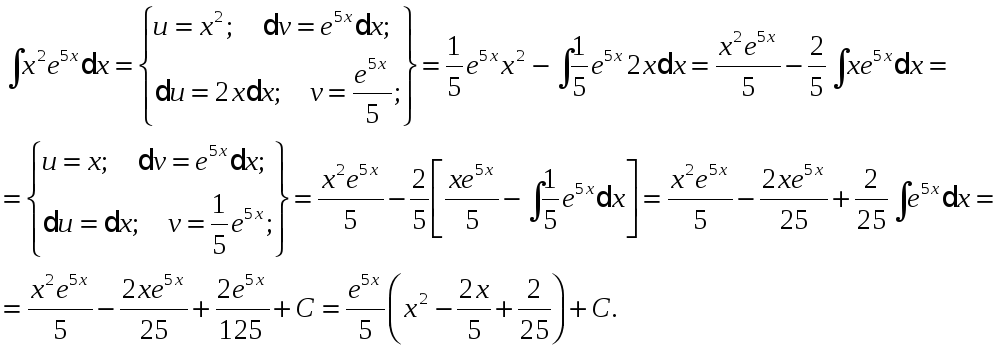
Приклад.
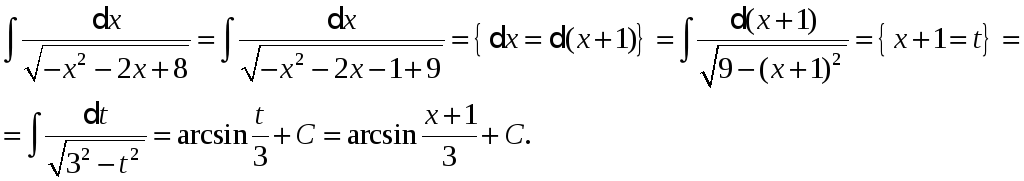
Приклад.
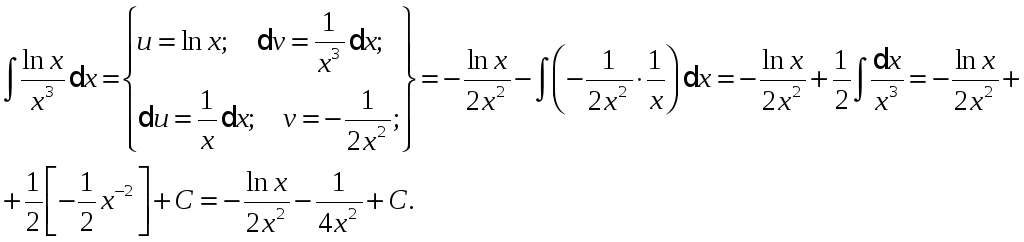
Приклад.
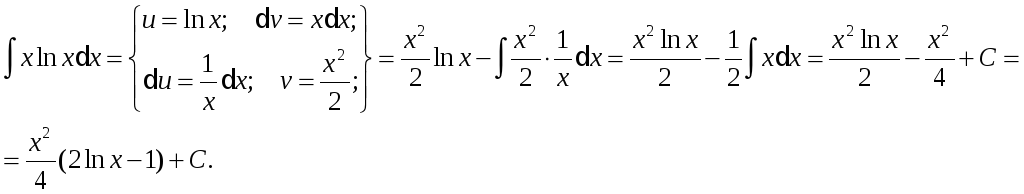
Приклад.
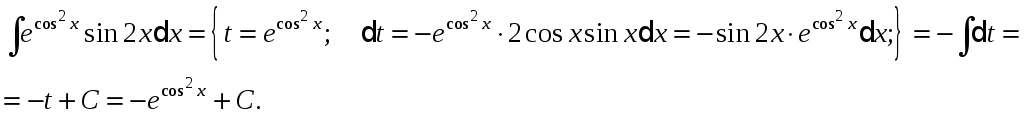
Приклад.
![]()
Приклад.
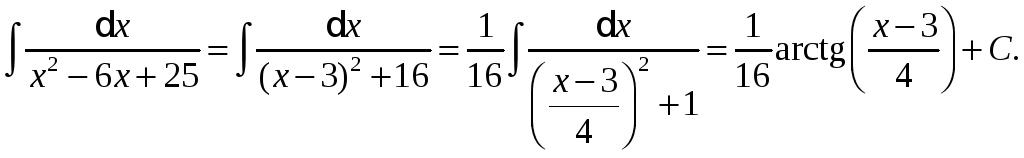
Інтегрування елементарних дробів.
Визначення: Елементарними називаються дроби наступних чотирьох типів:
I.
![]() III.
III.
![]()
II.
![]() IV.
IV.
![]()
m,
n –
натуральні числа (![]() )
і b2
– 4ac
<0.
)
і b2
– 4ac
<0.
Перші два типи інтегралів від елементарних дробів досить просто приводяться до табличних підстановкою t = ax + b.
II. ![]()
Розглянемо метод інтегрування елементарних дробів виду III.
Інтеграл дробу виду III може бути представлений у вигляді:
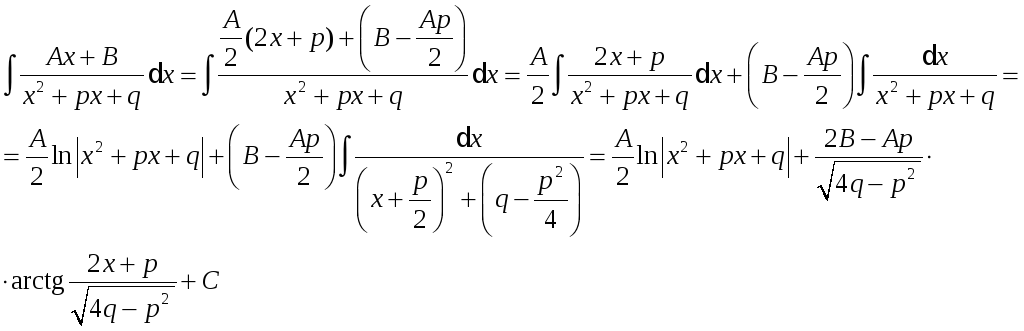
Тут у загальному вигляді показане приведення інтеграла дробу виду III до двох табличних інтегралів.
Розглянемо застосування зазначеної вище формули на прикладах.
Приклад.
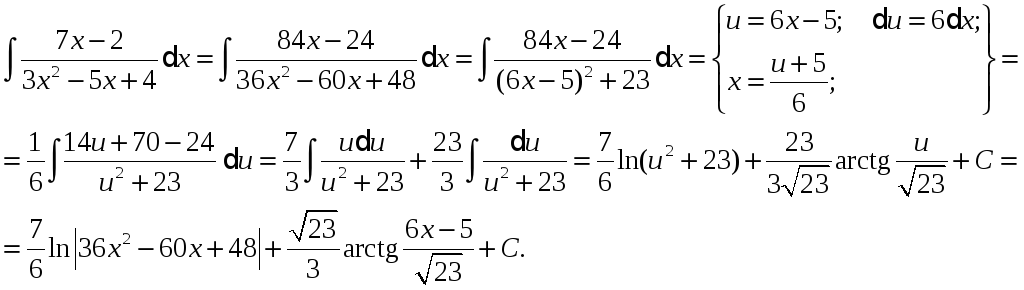
Загалом кажучи, якщо в тричлена ax2 + bx + c вираз b2 – 4ac >0, то дріб за визначенням не є елементарним, однак, його можна інтегрувати зазначеним вище способом.
Приклад.
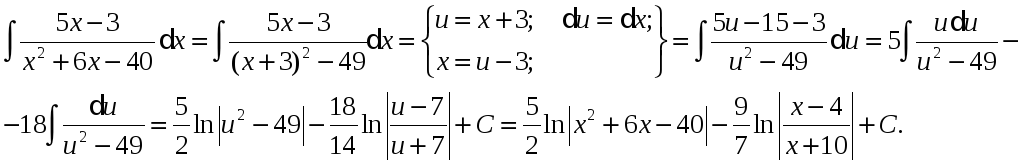
Приклад.
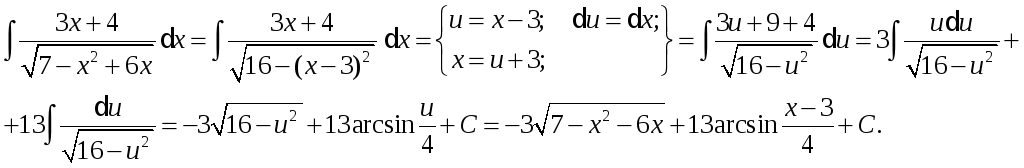
Розглянемо тепер методи інтегрування найпростіших дробів IV типу.
Спочатку розглянемо окремий випадок при М = 0, N = 1.
Тоді
інтеграл виду
![]() можна шляхом виділення в знаменнику
повного квадрата представити у вигляді
можна шляхом виділення в знаменнику
повного квадрата представити у вигляді
![]() .
Зробимо наступне перетворення:
.
Зробимо наступне перетворення:
![]() .
.
Другий інтеграл, що входить у цю рівність, будемо брати частинами.
Позначимо:

![]()
Для вихідного інтеграла одержуємо:
![]()
![]()
Отримана формула
називається рекурентною.
Якщо застосувати її n
– 1 раз, то вийде табличний інтеграл
![]() .
.
Повернемося тепер до інтеграла від елементарного дробу виду IV у загальному випадку.
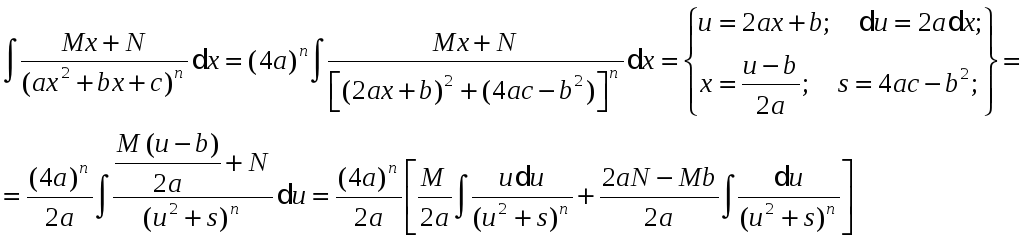
В
отриманій рівності перший інтеграл за
допомогою підстановки t
= u2
+ s
приводиться до табличного
![]() ,
а до другого інтеграла застосовується
розглянута вище рекурентна формула.
,
а до другого інтеграла застосовується
розглянута вище рекурентна формула.
Незважаючи на видиму складність інтегрування елементарного дробу виду IV, на практиці його досить легко застосовувати для дробів з невеликим ступенем n, а універсальність і загальність підходу уможливлює дуже просту реалізацію цього методу на ЕОМ.
Приклад: