
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
Вопросы для самопроверки
1. Что называется рангом матрицы? Как его можно найти?
2. Какая матрица называется обратной для данной матрицы?
3. Какие матрицы имеют обратные?
4. Как можно найти обратную матрицу?
5. В чем состоит матричный способ решения систем линейных уравнений?
Задачи для самостоятельного решения
Дана матрица А. Найти обратную матрицу.
1) EMBED Equation.3
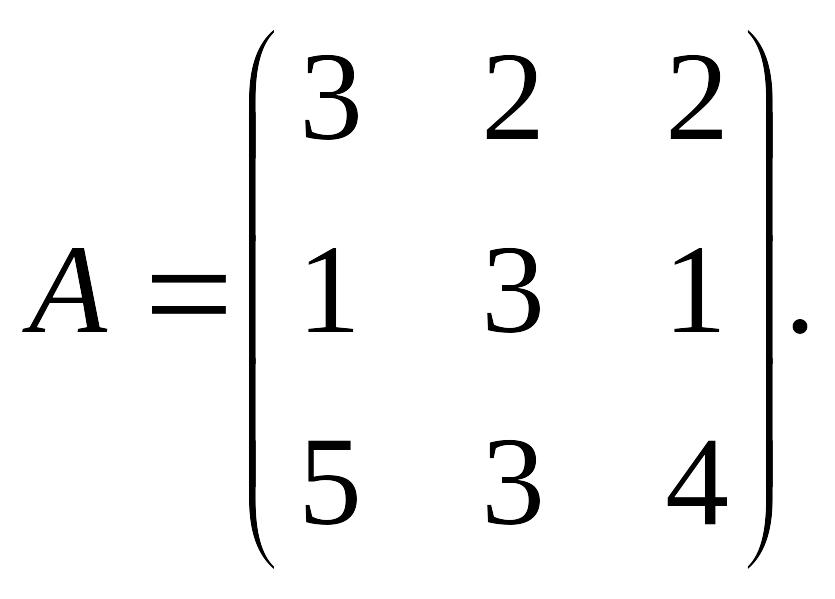 ;
2) EMBED Equation.3
;
2) EMBED Equation.3

3) EMBED Equation.DSMT4
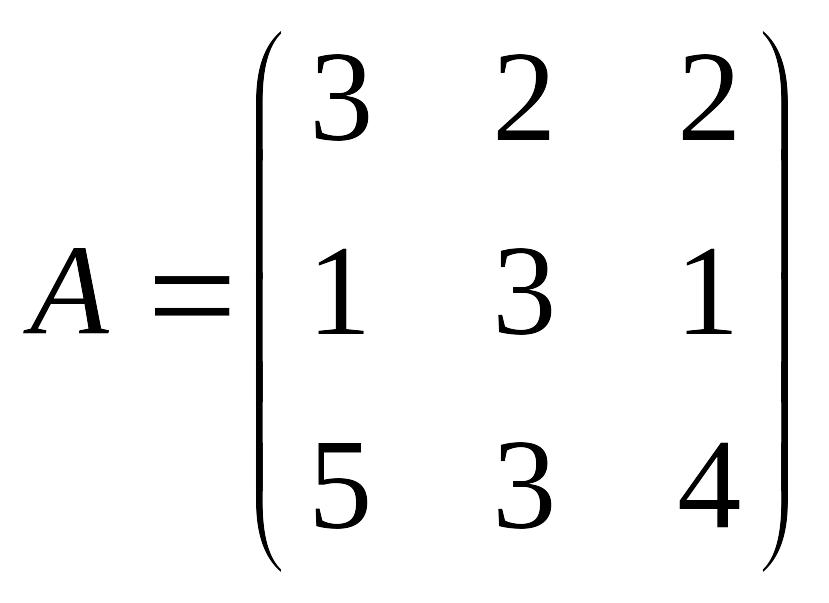 .
.
2. Определить ранг матрицы:
1) EMBED Equation.DSMT4
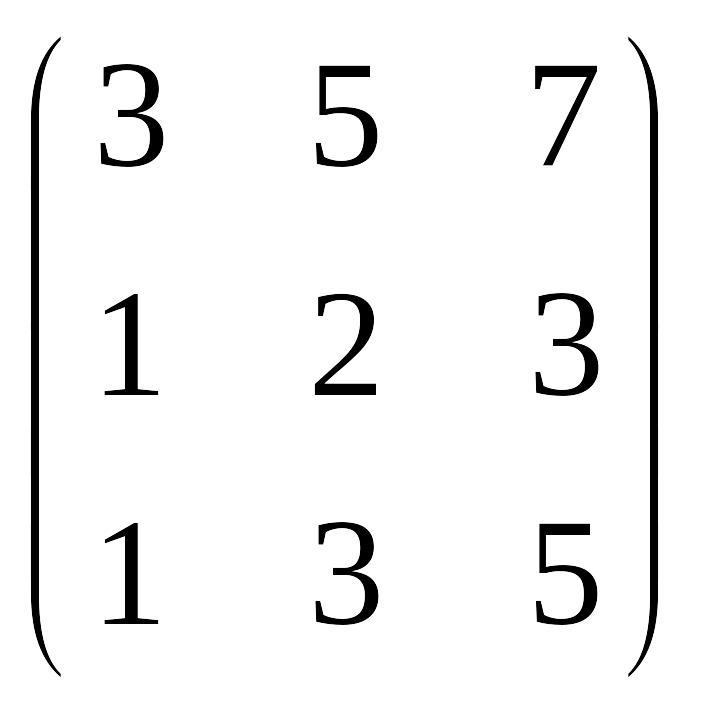 .
2) EMBED Equation.DSMT4
.
2) EMBED Equation.DSMT4
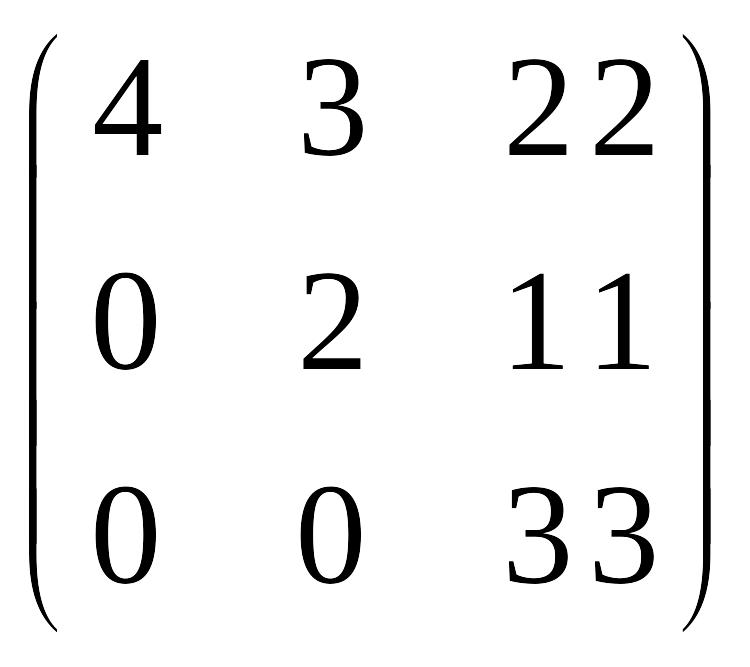 3) EMBED Equation.DSMT4
3) EMBED Equation.DSMT4
 .
.
3. Определить ранг матрицы и найти базисные миноры.
1) EMBED
Equation.DSMT4
 ;
2) EMBED Equation.DSMT4
;
2) EMBED Equation.DSMT4

Ответы:
1. 1)
EMBED Equation.3

2)
EMBED Equation.3

3)
EMBED Equation.DSMT4
 .
.
2. 1) r(A) =2; 2) r(A) =3; 3) r(A) =3.
3. 1) r(A) =2; базисными минорами являются
EMBED Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() EMBED Equation.DSMT4
EMBED Equation.DSMT4
![]() EMBED Equation.DSMT4
EMBED Equation.DSMT4
![]() ,
,
EMBED
Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() ,
EMBED Equation.DSMT4
,
EMBED Equation.DSMT4
![]() /
/
EMBED Equation.DSMT4
![]() 2)
r(A)
=3; базисными минорами являются
2)
r(A)
=3; базисными минорами являются
EMBED
Equation.DSMT4
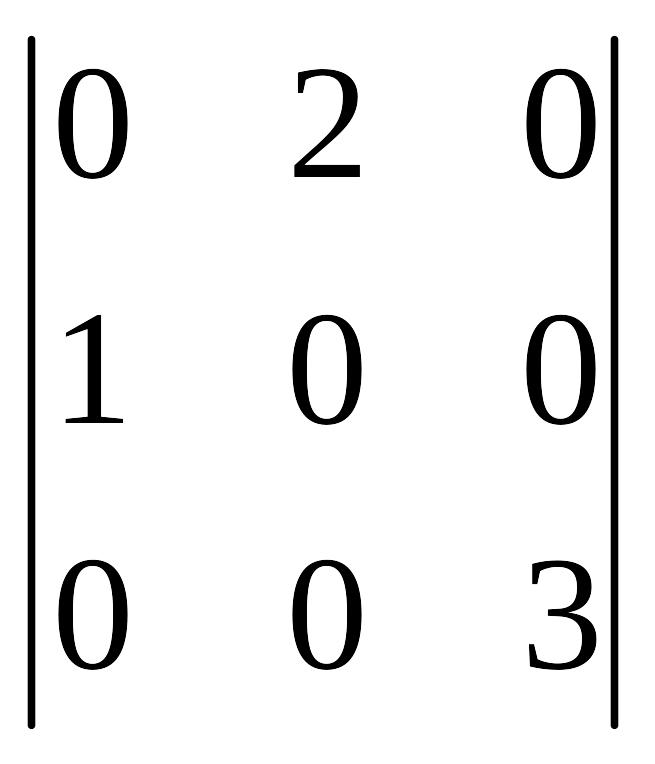 и EMBED Equation.DSMT4
и EMBED Equation.DSMT4
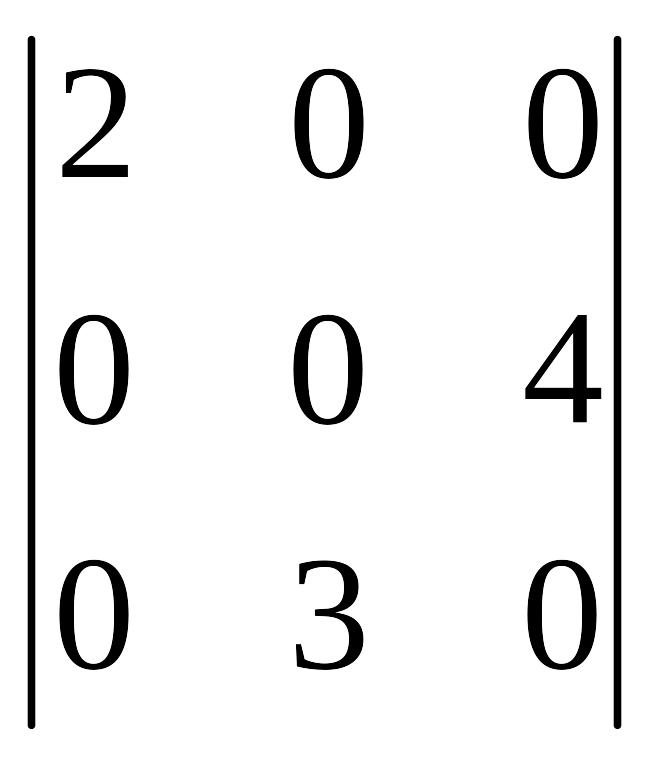 .
.
Занятие 4. Метод Гаусса решения систем линейных уравнений
Формулы
Крамера просты по своей записи, но при
больших n
они приводят к громоздким вычислениям.
Кроме того, они, в основном, используются,
когда число уравнений равно числу
неизвестных и EMBED Equation.3
![]() .
.
При решении систем, содержащих более трех уравнений, гораздо удобнее использовать метод последовательного исключения переменных (метод Гаусса). Пусть дана система:
EMBED
Equation.3
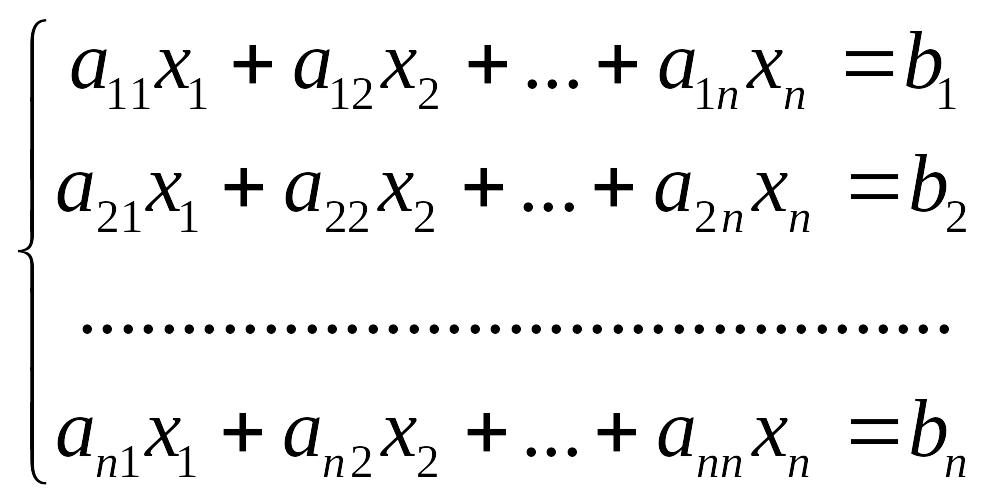 (4.1)
(4.1)
Элементарными преобразованиями системы называются следующие операции:
1.
умножение обеих частей одного из
уравнений системы на произвольное число
EMBED Equation.3
![]() .
.
2. прибавление к обеим частям одного из уравнений соответствующих частей другого уравнения, умноженного на число EMBED Equation.3 .
3. перестановки уравнений в системе.
Очевидно, что в результате каждой из этих операций система (4.10) перейдет в систему, эквивалентную исходной.
Выпишем матрицу системы (4.1):
EMBED
Equation.3
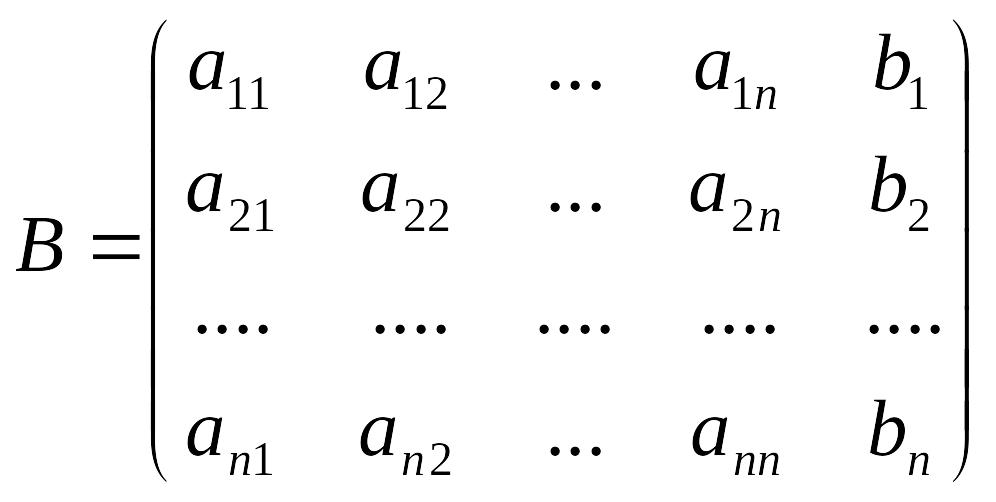
Если в системе (4.1) выполнено преобразование (2), то получим новую систему с матрицей В|, причем В| получается из В следующим образом: к некоторой строке матрицы В прибавляется другая строка, умноженная на λ; и т.д..
Поэтому вместо того, чтобы писать новую систему уравнений, пишут соответствующую ей матрицу В. При этом возможны следующие случаи:
1. Система преобразуется к «треугольному виду», тогда она имеет единственное решение.
2. В преобразованной системе число уравнений может оказаться меньше числа переменных. Такая система преобразуется к «трапецевидной» форме. Система (4.1) имеет бесчисленное множество решений.
3. В ходе исключения получается противоречивое уравнение. Тогда система (4.1) несовместна.
Пример 4.1. Решить систему уравнений:
EMBED Equation.3
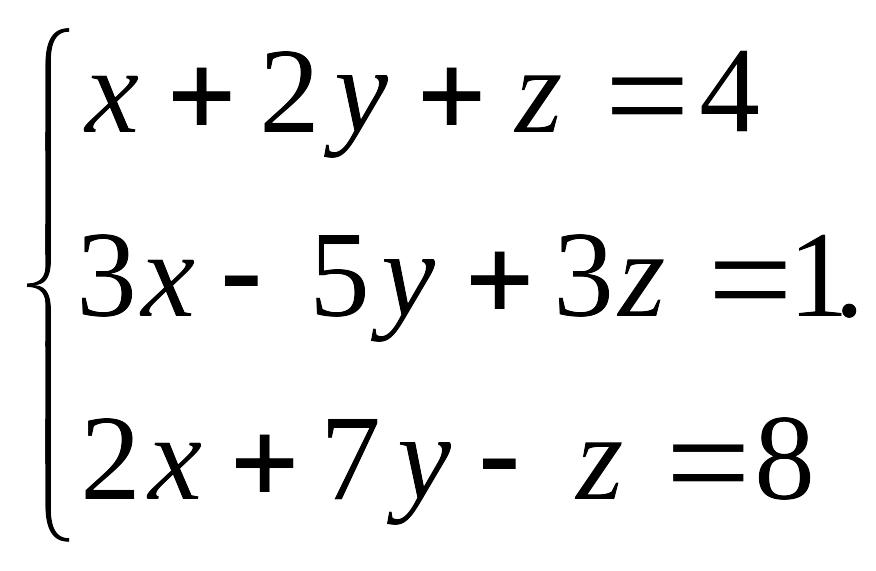
Решение. Расширенная матрица системы
 EMBED Equation.3
EMBED Equation.3
 ~
~
Умножаем каждый элемент 1-й строки на(-3) и складываем со 2-й строкой. Умножаем каждый элемент 1-й строки на(-2) и складываем с 3-й строкой. Получаем:
 EMBED Equation.3
EMBED Equation.3
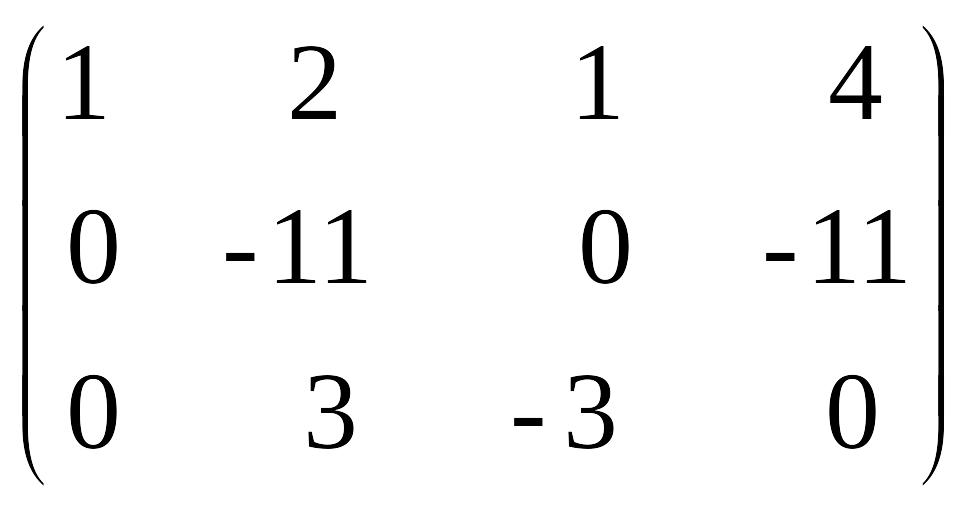 ~
Умножаем каждый элемент 2-й строки на (
EMBED Equation.3
~
Умножаем каждый элемент 2-й строки на (
EMBED Equation.3
![]() )
и складываем с 3-й строкой. Получаем:
)
и складываем с 3-й строкой. Получаем:
~ EMBED Equation.3
EMBED Equation.3
 .
.
Матрица привелась к «треугольному» виду. Система имеет единственное решение. Вернемся к системе уравнений.
EMBED
Equation.3
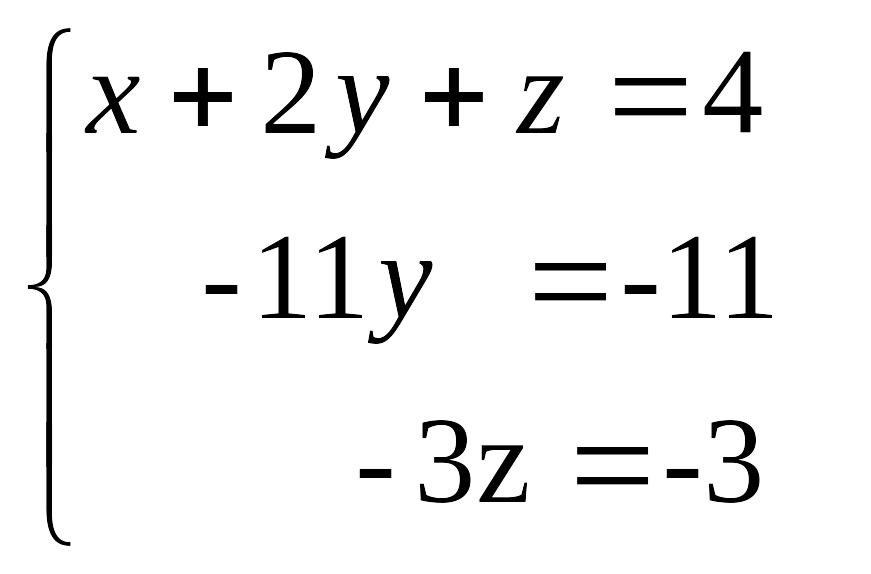
Из последнего уравнения получим z = 1. Подставим найденное значение во второе уравнение, найдем y=1 , а затем в первое. Таким образом, поднимаясь по системе от последнего уравнения к первому, найдем ее решение.
Решение системы: z = 1; y=1; x=1.
Пример 4.2. Решить систему уравнений:
EMBED Equation.3
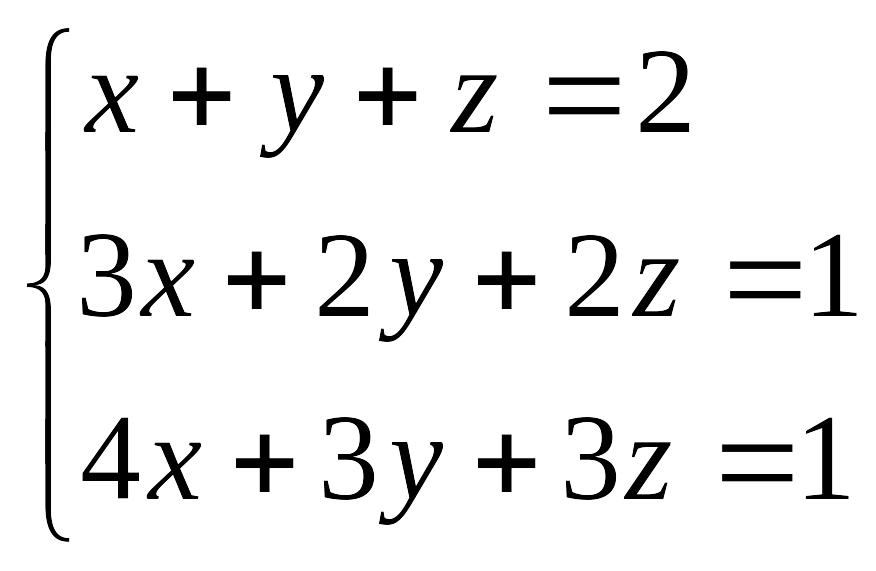
Решение. Расширенная матрица системы
 EMBED Equation.3
EMBED Equation.3
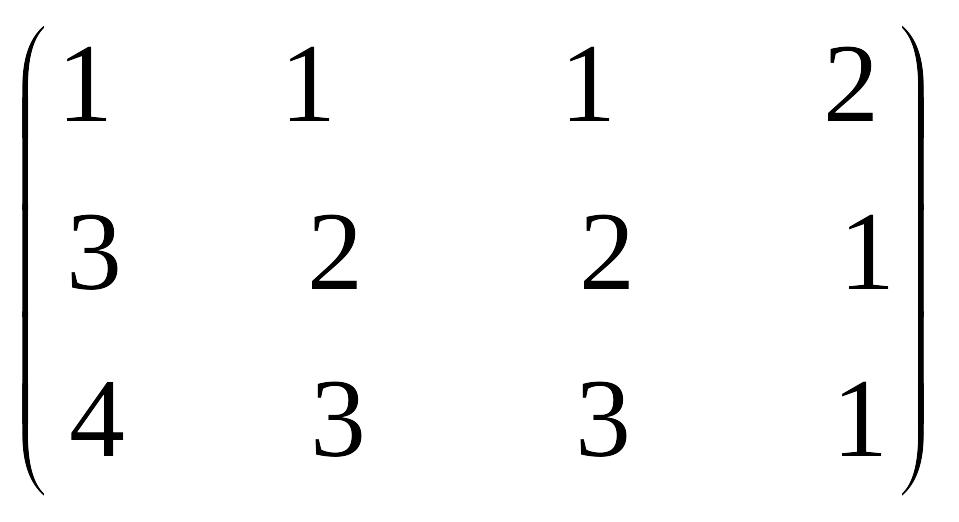 ~
Умножаем
каждый элемент 1-й
~
Умножаем
каждый элемент 1-й
строки на(-3) и на (-4) и сложим со второй и третьей строкой соответственно. Получим :
~
EMBED Equation.3
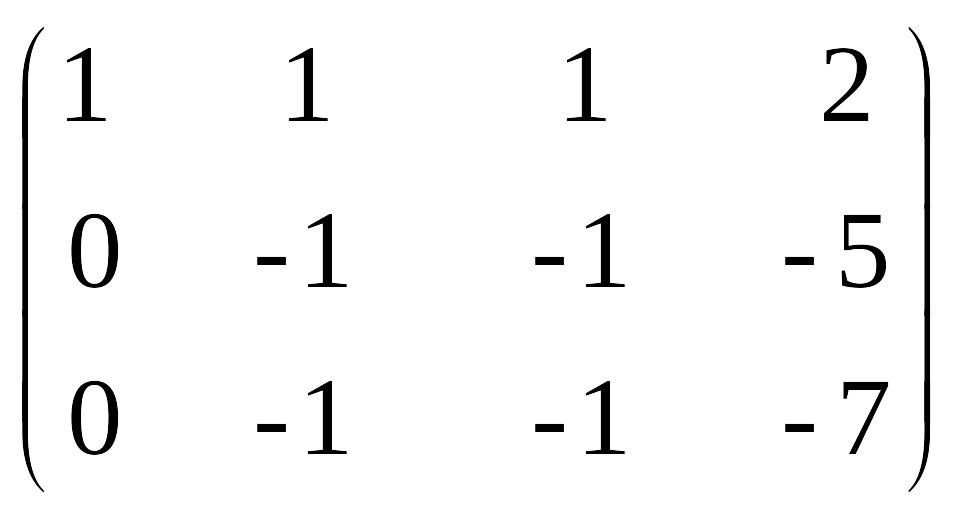 ~
Умножаем каждый элемент 2-й
~
Умножаем каждый элемент 2-й
строки на(-1) и сложим с 3-й. Получим :
~
EMBED Equation.3
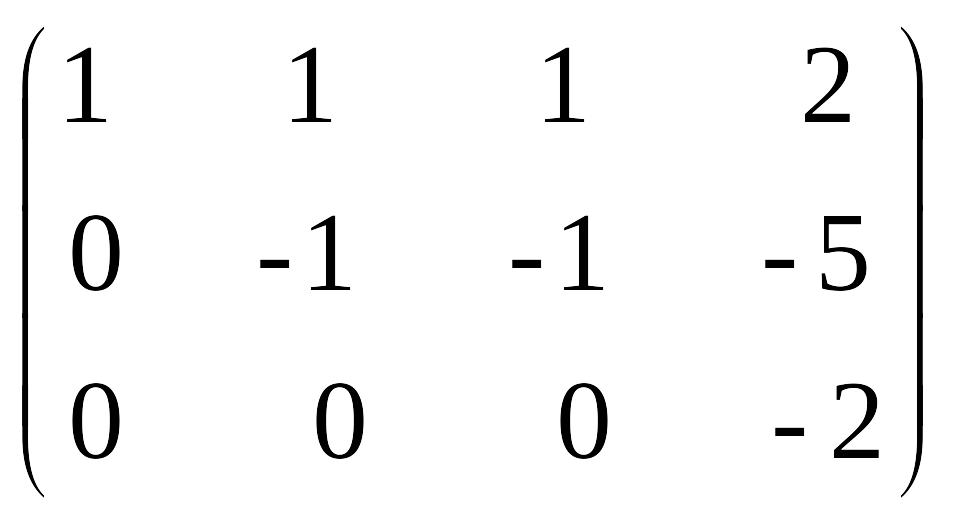 .
.
Третье уравнение системы противоречиво. С другой стороны,
ранг матрицы системы r(A)=2, ранг расширенной матрицы r(A/B)=3, r(A)≠r(A/B), следовательно, система несовместна.
Пример 4.3. Решить систему уравнений:
EMBED Equation.3
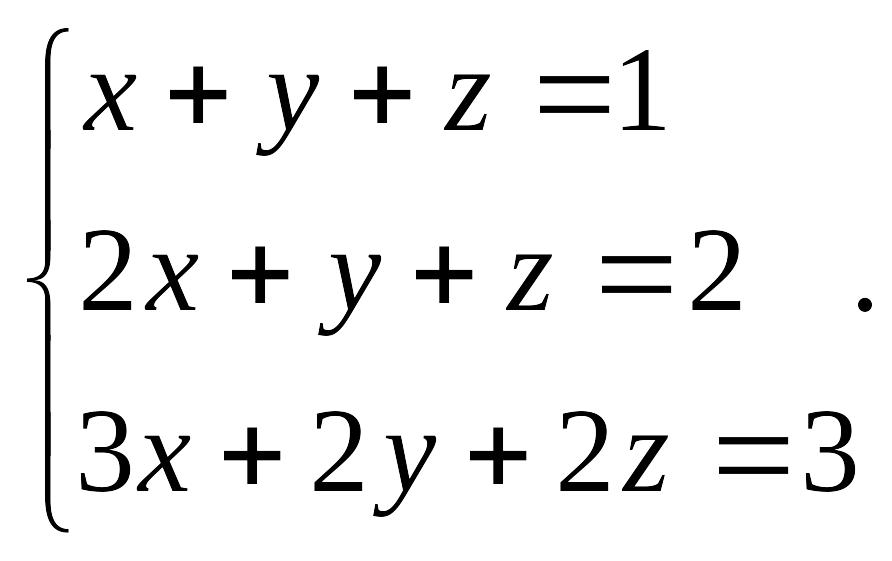
Решение. Расширенная матрица системы
EMBED Equation.3
 ~
EMBED
Equation.3
~
EMBED
Equation.3
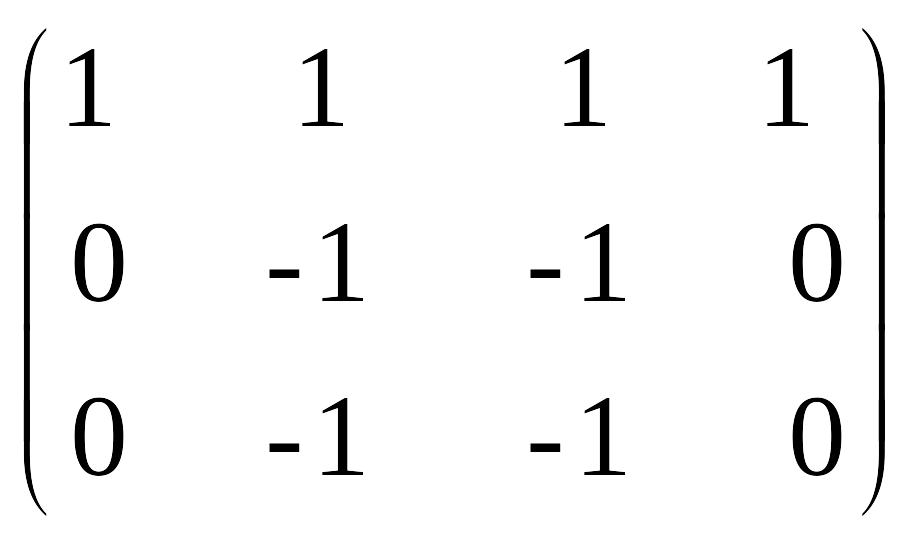 ~
EMBED Equation.3
~
EMBED Equation.3
EMBED Equation.3
~
EMBED Equation.3
~
EMBED Equation.3
EMBED Equation.3
 ,
,
Матрица привелась к «трапецевидной» форме
r(A)=2; r(A/B)= 2 => система совместна и имеет бесчисленное множество решений. Тогда
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
Пусть z = t, t- любое число, тогда x =1, y = -t, z = t , t – любое число.
Однородная система имеет либо единственное тривиальное решение, т.е. x = y = z = 0, если EMBED Equation.3 ≠0 и ранг матрицы равен числу неизвестных, причем число неизвестных равно числу уравнений, либо имеет бесчисленное множество решений в противном случае.
