
- •1.1. Понятие определителя
- •Пусть дана матрица
- •1.2. Основные свойства определителя
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •2.1. Определения
- •2.2. Решение систем линейных уравнений
- •2.3. Однородные системы
- •2.4. Действия над матрицами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •3.1. Вычисление ранга матрицы
- •Матрица (3.1) имеет ступенчатый вид, где embed Equation.3 , * - некоторые числа.
- •3.2. Вычисление обратной матрицы
- •3.3. Матричная форма системы уравнений.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •5.1. Понятие вектора
- •5.2. Линейные операции над векторами
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •6.1. Проекции вектора на ось. Свойства проекций
- •6.2. Декартова прямоугольная система координат
- •6.3. Действия над векторами в координатах.
- •6.4. Координаты вектора
- •6.5. Условие коллинеарности векторов в координатной форме.
- •6.6. Деление отрезка в данном отношении.
- •6.7. Разложение вектора по базису
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства скалярного произведения
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Алгебраические свойства векторного произведения
- •Пример 8.1. Упростить выражение
- •Находим площадь треугольника
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •10.1. Общее уравнение плоскости.
- •10.2. Нормальное уравнение плоскости.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •11.1. Уравнение плоскости в отрезках.
- •11.2. Уравнение плоскости, проходящей через три точки.
- •11.3. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •Задачи для самостоятельного решения
- •12.1. Общее и канонические уравнения прямой в пространстве.
- •12.2. Уравнение прямой, проходящей через две заданные точки.
- •12.3. Параметрические уравнения прямой.
- •12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •13.1. Условие принадлежности двух прямых к одной плоскости.
- •13.2. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •13.3. Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •14.1. Общее уравнение прямой.
- •14.2. Каноническое уравнение прямой.
- •14.3. Параметрические уравнения прямой.
- •14.4. Уравнение прямой с угловым коэффициентом.
- •14.5. Угол между двумя прямыми.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •15.2. Эллипс.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •16 1. Гипербола.
- •16.2. Парабола.
- •Задачи для самостоятельного решения
- •Типовые расчеты
- •Правила выполнения и оформления типовых расчетов
- •1 . Матрицы. Определители. Системы линейных уравнений
- •2. Векторная алгебра
- •Аналитическая геометрия
- •4. Аналитическая геометрия на плоскости
- •2.15. Через точку м (2,-1) провести прямую, параллельную прямой embed Equation.3
- •5. Кривые второго порядка
- •Библиографический список
- •Оглавление
- •394026 Воронеж, Московский просп., 14
2.3. Однородные системы
Однородной называется система вида
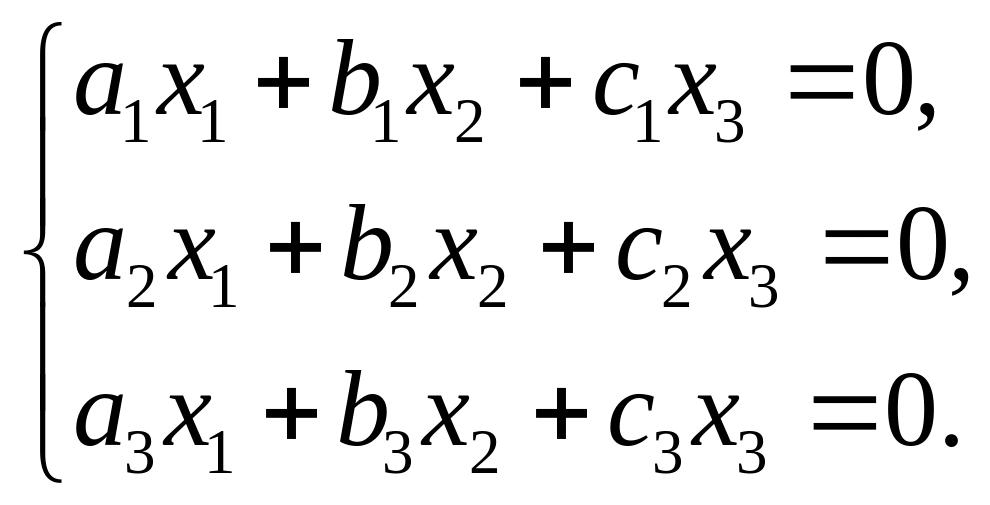 (2.5)
(2.5)
Очевидно, что всякая однородная система имеет решение
x= 0, y=0, z= 0, называемое нулевым Теорема Крамера изменится:
1) если , система однородных линейных уравнений (2.5) имеет только нулевое решение;
2) если , система имеет бесчисленное множество решений;
Запишем
эти решения. Пусть
![]()
 Перепишем систему уравнений
Перепишем систему уравнений
![]()
И решим ее по формулам Крамера

 .
.
Переменная
![]() может быть выбрана произвольно, а две
другие переменные находятся по полученным
формулам. Система имеет бесчисленное
множество решений.
может быть выбрана произвольно, а две
другие переменные находятся по полученным
формулам. Система имеет бесчисленное
множество решений.
Пример 2.2. Решить систему уравнений
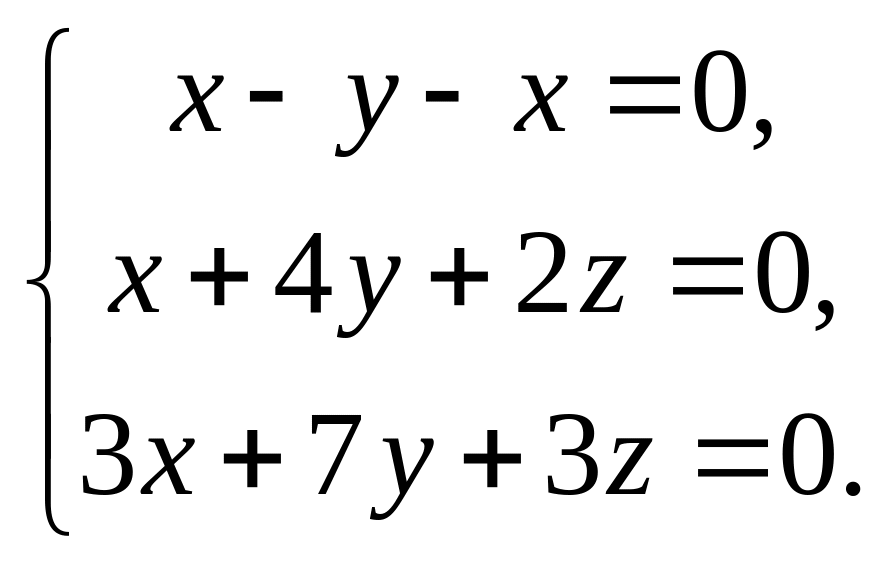
Определитель системы равен нулю. Система имеет бесчисленное множество решений. Перепишем систему
![]()
Решим полученную систему по формулам Крамера.
![]()
![]() Придавая
z
различные значения, получим бесчисленное
множество решений.
Придавая
z
различные значения, получим бесчисленное
множество решений.
2.4. Действия над матрицами
1. Суммой матриц А и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Представим это в сокращенной записи. Пусть
А=![]() ,
В
=
;
i
=1, 2, …, m,
j
=1, 2, …, n.
,
В
=
;
i
=1, 2, …, m,
j
=1, 2, …, n.
Тогда сумма этих матриц С = А + В имеет вид
С=![]() ,
,
![]() i
=1, 2, …, m,
j
=1, 2, …, n.
i
=1, 2, …, m,
j
=1, 2, …, n.
Пусть А, В, С – матрицы, имеющие одинаковый размер. Операция суммирования матриц обладает следующими свойствами
1.
А+В=В+А.
2. (А+В)+С=А+(В+С).
3. А+О=А, где О – нулевая матрица.
Пример 2.3. Пусть даны матрицы А и В:
А
=![]() ,
В
=
,
В
=![]() .
.
Тогда их суммой, согласно определению, является матрица
С
=![]() ,
С=
,
С=![]() .
.
2.
Произведением
матрицы А на число
называется матрица В=
А,
которая получается из матрицы А
умножением всех ее элементов на
§:
EMBED Equation.3
![]()
Пусть
А, В, С –
матрицы,
имеющие одинаковый размер, а EMBED
Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() - некоторые вещественные числа. Тогда:
- некоторые вещественные числа. Тогда:
1.
EMBED Equation.3
![]()
2.
EMBED Equation.3
![]()
3.
EMBED Equation.3
![]()
4.ОА=О, где О – нулевая матрица.
Пример
2.4. Пусть
даны матрица А
и число EMBED
Equation.3
![]() :
:
А
= EMBED
Equation.3
![]() ,
EMBED Equation.3
=2.
,
EMBED Equation.3
=2.
Тогда произведением матрицы А на число EMBED Equation.3 является матрица
С
= EMBED Equation.3
![]() .
.
3.Произведением
АВ
двух квадратных матриц
А
и В
одного порядка называется третья
квадратная матрица
С
того же порядка, составленная по
следующему правилу: элемент EMBED Equation.3
![]() ,
стоящий в матрице С
на пересечении k-й
строки с l-м
столбцом,
есть сумма произведений элементов
EMBED Equation.3
,
стоящий в матрице С
на пересечении k-й
строки с l-м
столбцом,
есть сумма произведений элементов
EMBED Equation.3
![]() строки матрицы А
на соответствующие элементы l-го
столбца матрицы В:
строки матрицы А
на соответствующие элементы l-го
столбца матрицы В:
EMBED
Equation.3
![]() .
(2.6)
.
(2.6)
Определение
произведения можно распространить на
неквадратные матрицы, у которых число
столбцов
матрицы множимого А
равно числу
строк
матрицы множителя EMBED Equation.3
![]() .
При соблюдении этого условия множимого
А
может иметь любое число (m)
строк, а матрица В
– любое число
(n)
столбцов. Матрица С
= АВ будет
иметь m
строк и n
столбцов, ее элементы вычисляются по
формуле (2.6).
.
При соблюдении этого условия множимого
А
может иметь любое число (m)
строк, а матрица В
– любое число
(n)
столбцов. Матрица С
= АВ будет
иметь m
строк и n
столбцов, ее элементы вычисляются по
формуле (2.6).
Пример 2.5. Найти произведения АВ и ВА матриц
А
= EMBED Equation.3
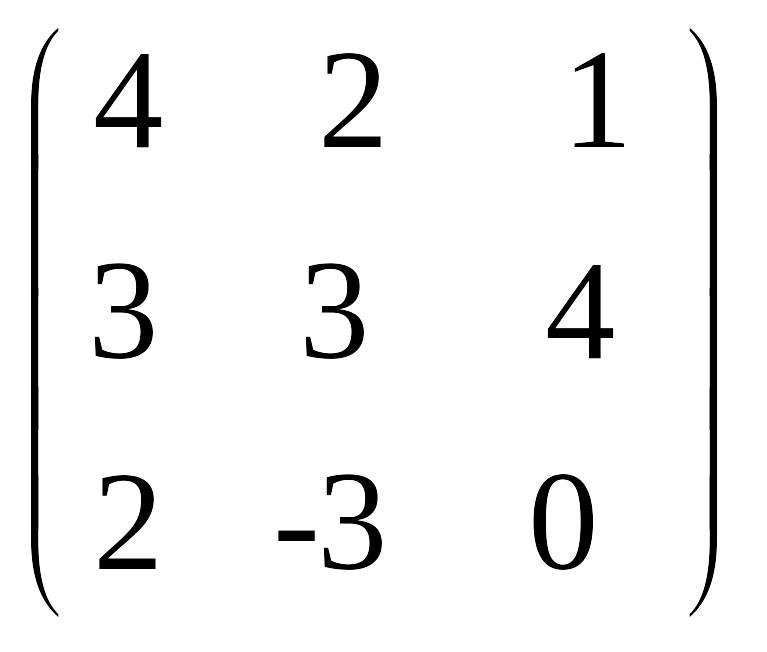 ,
В
= EMBED Equation.3
,
В
= EMBED Equation.3

Решение. По формуле (2.6) получаем элементы
матрицы АВ:
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]()
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]()
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]()
Итак,
АВ
= EMBED Equation.3
 ;
;
По формуле (2.6) получаем элементы матрицы ВА:
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]()
EMBED
Equation.3
![]() EMBED Equation.3
EMBED Equation.3
![]()
EMBED
Equation.3
![]()
Итак, ВА=
EMBED Equation.3
 .
.
Сравнивая
матрицы АВ
и ВА
и пользуясь
определением равенства матриц, заключаем,
что EMBED Equation.3
![]() .
.
Пример 2.6. Найти произведения АВ матриц
А
= EMBED Equation.3
![]() ,
В = EMBED Equation.3
,
В = EMBED Equation.3
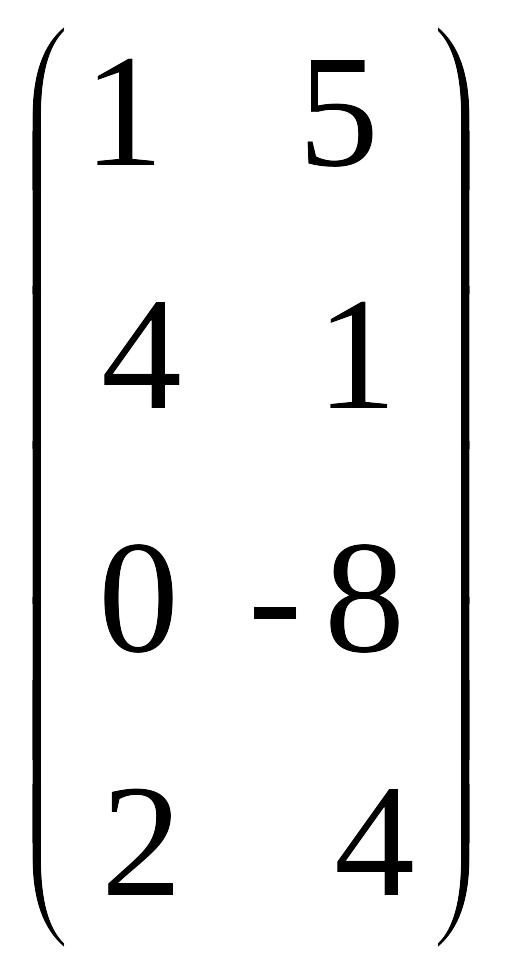 .
.
Решение. Число столбцов матрицы А равно числу строк матрицы EMBED Equation.3 , поэтому можно умножать матрицу А на матрицу EMBED Equation.3 . По формуле (2.6) находим:
EMBED
Equation.3
![]()
EMBED
Equation.3
![]()
EMBED
Equation.3
![]()
EMBED
Equation.3
![]()
Следовательно:
АВ
= EMBED Equation.3
![]() .
.
Пусть А, В и С – матрицы соответствующих размеров (чтобы произведение матриц были определены), а EMBED Equation.3 - действительное число. Тогда имеют место следующие свойства произведения матриц:
АВ EMBED Equation.3
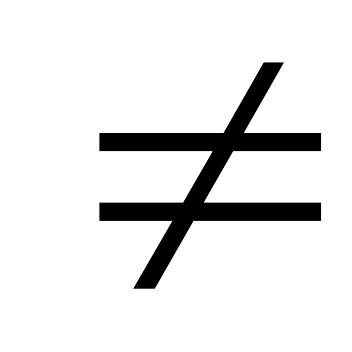 ВА
ВА
2. (АВ)С = А(ВС).
3. (А + В)С = АС + ВС.
4. А(В + С) = АВ + АС.
5. EMBED Equation.3 (АВ) = ( EMBED Equation.3 А)В = А( EMBED Equation.3 В).
Нетрудно
убедиться, что в алгебре квадратных
матриц единичная матрица EMBED Equation.3
![]() играет роль единицы, т.е. можно отметить
еще два свойства, связанных с умножением
на эту матрицу слева и справа:
играет роль единицы, т.е. можно отметить
еще два свойства, связанных с умножением
на эту матрицу слева и справа:
6. АЕ = А.
7. ЕА = А.
Иными словами, произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу.
