Задачи для самостоятельного решения
1.
Составить уравнение гиперболы, проходящей
через точку М(9;
8), если асимптоты гиперболы имеют
уравнения
EMBED Equation.3
.
Ответ:
EMBED Equation.3
.
2.
Найти уравнение гиперболы, вершины и
фокусы которой находятся в соответствующих
фокусах и вершинах эллипса
EMBED Equation.3
.
Ответ:
EMBED Equation.3
.
3. Через точку М(0;-1) и правую вершину гиперболы
Зх2- 4у2=12 проведена прямая. Найти вторую точку пересечения прямой с гиперболой.
Ответ: N(-4; -3).
4. Дана гипербола х2 - у2=8. Найти софокусный эллипс, проходящий через точку М (4, 6).
Ответ:
EMBED Equation.3
.
5. Дан эллипс 9х2 + 25у2=1. Написать уравнение софокусной равнобочной гиперболы.
Ответ:
EMBED Equation.3
.
6.
Составить уравнение гиперболы, если ее
эксцентриситет равен 2 и фокусы
совпадают с фокусами эллипса EMBED
Equation.3
.
7.
Составить простейшее уравнение параболы,
если известно, что ее фокус находится
в точке пересечения прямой EMBED Equation.3
с осью Ох.
Ответ.
EMBED Equation.3
.
8.
На параболе EMBED Equation.3
найти точку, расстояние которой от
директрисы параболы равно 4.
Ответ.
EMBED Equation.3
и EMBED Equation.3
.
9.
Составить уравнение параболы с вершиной
в начале координат, симметричной
относительно оси Ох
и отсекающей
от прямой EMBED Equation.3
хорду длиной EMBED Equation.3
.
Ответ.
EMBED Equation.3
,
EMBED Equation.3
.
10.
Парабола EMBED Equation.3
отсекает от прямой, проходящей через
начало координат, хорду, равную EMBED
Equation.3
.
Составить уравнение этой прямой.
Ответ.
EMBED Equation.3
.
11. Составить простейшее уравнение параболы, если хорда, перпендикулярная к оси симметрии и делящая пополам расстояние между фокусом и вершиной, равна 1.
Ответ.
EMBED Equation.3
EMBED Equation.3
.
12.
На параболе EMBED Equation.3
найти точку, расстояние которой от
прямой EMBED Equation.3
равно 2.
Ответ.
EMBED Equation.3
Занятие 17. Преобразование координат и упрощение уравнений кривых второго порядка
17.1. Преобразование координат.
Перейдем
от системы координат Оху
к новой системе EMBED Equation.3
(направление
осей координат прежнее, за новое начало
координат принята точка EMBED Equation.3
b)).
Связь между старыми и новыми координатами
некоторой точки М
плоскости
определяется следующими формулами:
EMBED
Equation.3
или
EMBED
Equation.3
Первая
пара формул дает выражение старых
координат через новые, вторая-выражение
новых координат через старые. При
повороте осей координат на угол EMBED
Equation.3
(начало координат прежнее, причем
EMBED Equation.3
отсчитывается против часовой стрелки)
зависимость между старыми координатами
( х, у)
и новыми ( EMBED Equation.3
)
определяется следующими формулами:
EMBED
Equation.3
EMBED
Equation.3
Пример
17.1. Сделан
параллельный перенос осей координат,
причем новое начало расположено в точке
EMBED Equation.3
.
Известны старые координаты точки EMBED
Equation.3
Определить
новые координаты этой точки.
Решение.
Здесь EMBED Equation.3
b=-4,
х=7,
у=8.
Так
как EMBED Equation.3
EMBED Equation.3
b,
то EMBED Equation.3
=7-3=4,
EMBED Equation.3
8-(-4)=12.
Пример
17.2 На
плоскости Оху
дана точка М(4;3).
Систему координат повернули вокруг
начала координат так, что новая ось
прошла через точку М.
Определить
старые координаты точки А,
если известны
ее новые координаты EMBED Equation.3
,
EMBED Equation.3
Решение.
Так как EMBED Equation.3
,
то sin
EMBED
Equation.3
=
EMBED
Equation.3
,
cos
EMBED
Equation.3
;
получаем формулы преобразования
координат: EMBED Equation.3
EMBED
Equation.3
EMBED Equation.3
Положив
EMBED Equation.3
,
находим х=1,
у=7.
Пример 17.3. Привести уравнение кривой к каноническому виду
EMBED
Equation.3
.
Решение. Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем
EMBED
Equation.3
или
EMBED
Equation.3
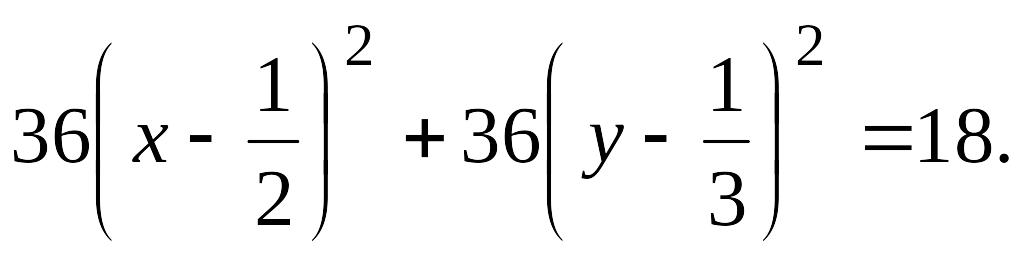Вводя новые координаты EMBED Equation.3
,
после деления на 18, получаем EMBED Equation.3
или EMBED Equation.3
.
Таким
образом, получено уравнение окружности
с центром в точке EMBED Equation.3
.
Пример
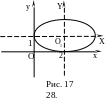
17.4. Привести
уравнение кривой к каноническому виду
и построить линию, определяемую уравнением
EMBED Equation.3
.
Решение. Выделяя полные квадраты , преобразуем левую часть уравнения. Имеем
EMBED
Equation.3
;
EMBED
Equation.3
;
EMBED
Equation.3
.
Вводя
новые координаты EMBED Equation.3
,
получаем EMBED Equation.3
.
Таким
образом, получено уравнение эллипса с
центром в точке EMBED Equation.3
.
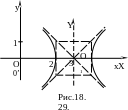
Пример
17.5. Привести
уравнение кривой к каноническому виду
и построить линию, определяемую уравнением
EMBED Equation.3
.
Решение. Выделяя полные квадраты , преобразуем левую часть уравнения. Имеем
EMBED
Equation.3
EMBED Equation.3
;
EMBED
Equation.3
.
Вводя
новые координаты EMBED Equation.3
,
получаем EMBED Equation.3
- уравнение гиперболы, для которой
действительной осью является ось EMBED
Equation.3
,
а центр расположен в точке EMBED Equation.3
.
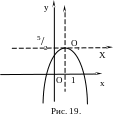
Пример
17.6. Привести
уравнение кривой к каноническому виду
и построить линию, определяемую уравнением
EMBED Equation.3
.
Решение. Выделяя полный квадрат, преобразуем левую часть уравнения. Имеем
EMBED
Equation.3
;
EMBED
Equation.3
;
EMBED
Equation.3
.
Вводя новые координаты
EMBED
Equation.3
,
получаем
EMBED Equation.3
Это
уравнение параболы, вершина которой в
точке EMBED Equation.3
.
Пример 17.7. Привести к каноническому виду уравнение
EMBED
Equation.3
Решение. 1). Преобразуем это уравнение, воспользовавшись формулами поворота осей координат
EMBED
Equation.3
EMBED Equation.3
Имеем
EMBED Equation.3
или
EMBED Equation.3
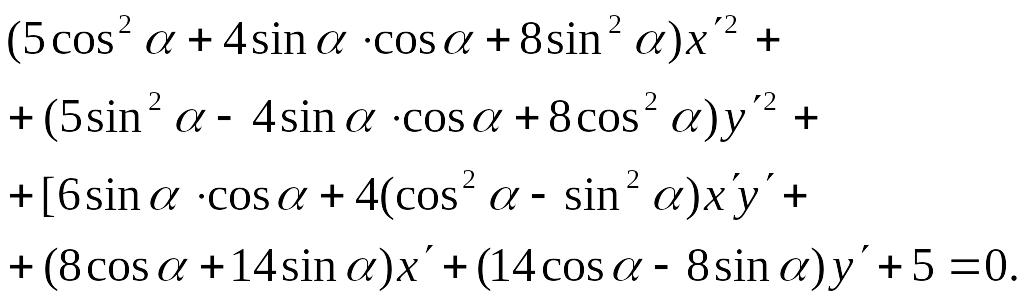
Найдём EMBED Equation.3 из условия
EMBED Equation.3
т.е.
приравниваем нулю коэффициент при
EMBED Equation.3
.
Получаем
уравнение
EMBED Equation.3
.Отсюда
EMBED Equation.3
Заметим,
что эти значения EMBED Equation.3
соответствуют двум взаимно перпендикулярным
направлениям. Поэтому, беря EMBED Equation.3
вместо
2, мы только меняем ролями оси EMBED
Equation.3
и
EMBED Equation.3
.
Пусть
EMBED
Equation.3
,
тогда EMBED Equation.3
EMBED Equation.3
возьмём
положительные значения EMBED Equation.3
и
EMBED Equation.3
Тогда уравнение принимает вид
EMBED Equation.3
или
EMBED Equation.3
2) Выражение в скобках дополним до полных квадратов:
EMBED Equation.3
или
EMBED Equation.3
Приняв
за новое начало точку EMBED Equation.3
применим
формулы преобразования координат EMBED
Equation.3
EMBED Equation.3
получим
EMBED Equation.3
или
EMBED Equation.3
(уравнение эллипса).
Пример 17.8. Привести к каноническому виду уравнение
EMBED
Equation.3
Решение. 1). Преобразуем это уравнение, воспользовавшись формулами поворота осей координат
EMBED Equation.3 EMBED Equation.3
Имеем
EMBED Equation.3
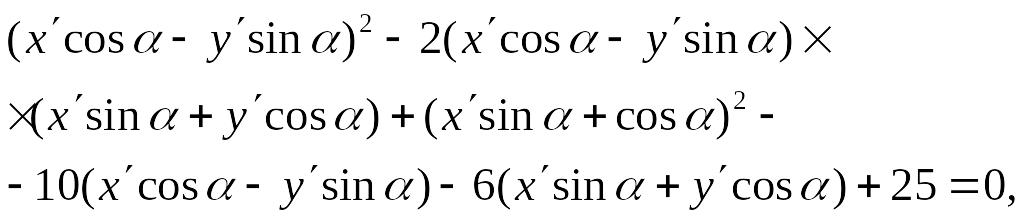
или
EMBED
Equation.3
Приравнивая
нулю коэффициент при EMBED Equation.3
,
получаем уравнение EMBED Equation.3
,
откуда EMBED Equation.3
,
т.е. EMBED Equation.3
Пусть
EMBED
Equation.3
,
тогда EMBED Equation.3
EMBED Equation.3
.
Тогда уравнение принимает вид
EMBED
Equation.3
или
EMBED
Equation.3
2) Выражение в скобках дополним до полного квадрата:
EMBED
Equation.3
или EMBED Equation.3
Приняв
за новое начало, точку EMBED Equation.3
применим
формулы преобразования координат EMBED
Equation.3
EMBED Equation.3
получим
EMBED Equation.3
(уравнение параболы).
Вопросы для самопроверки
Каковы канонические уравнения эллипса, гиперболы, параболы?
Что называется фокусами, директрисами и эксцентриситетом эллипса, гиперболы, параболы?
Каковы геометрические свойства эллипса, гиперболы, параболы?
Что называется асимптотами гиперболы?
Каков геометрический смысл неравенства первой степени с двумя переменными?
Задачи для самостоятельного решения
1. Привести уравнения кривых к каноническому виду и построить линии, определяемые уравнениями:
1)
EMBED Equation.3
;
2)
EMBED Equation.3
3)
EMBED Equation.3
4)
EMBED Equation.3
5)
EMBED Equation.3
6)
EMBED Equation.3
Ответы:
1)
EMBED Equation.3
,
новое начало EMBED Equation.3
2)
EMBED Equation.3
,
новое начало EMBED Equation.3
3)
EMBED Equation.3
,
новое начало EMBED Equation.3
4)
EMBED Equation.3
,
новое начало EMBED Equation.3
5)
EMBED Equation.3
;
новое начало
EMBED Equation.3
6)
EMBED Equation.3
;
новое начало EMBED Equation.3
.
2. Привести уравнения кривых к каноническому виду и построить линии, определяемые уравнениями:
1)
EMBED Equation.3
2)
EMBED Equation.3
Ответы:
1)
EMBED
Equation.3
2)
EMBED
Equation.3
.