6.3. Действия над векторами в координатах.

Пусть даны координаты двух радиусов-векторов EMBED Equation.3 и EMBED Equation.3 или EMBED Equation.3 и EMBED Equation.3

1. два радиус-вектора равны EMBED Equation.3 тогда и только тогда, когда равны их координаты

EMBED Equation.3

2. Чтобы умножить радиус-вектор на число, надо каждую из его координату умножить на это число:

EMBED Equation.3 или EMBED Equation.3 , т.к.

EMBED Equation.3 и т.д. – по первому свойству проекций.

3. Чтобы сложить (вычесть) два радиус-вектора, надо сложить (вычесть) их одноименные координаты.

EMBED Equation.3 или EMBED Equation.3 ;

т.к. EMBED Equation.3 и т.д. – по второму свойству проекций.

6.4. Координаты вектора

Пусть даны координаты точек EMBED Equation.3 и EMBED Equation.3 .

Н айдем координаты вектора EMBED Equation.3 . Рассмотрим радиус-векторы: EMBED Equation.3 и EMBED Equation.3 .

Очевидно, что

EMBED Equation.3 . В координатной форме:

EMBED Equation.3 . (6.5)

Следовательно, чтобы найти координаты вектора EMBED Equation.3 , нужно из координат его конца вычесть координаты начала.

6.5. Условие коллинеарности векторов в координатной форме.

Пусть EMBED Equation.3 и EMBED Equation.3 - коллинеарные векторы. Тогда EMBED Equation.3 .

EMBED Equation.3 (5.6)

Т.е. векторному равенству соответствует три равенства (5.6) для координат. Если векторы пропорциональны, то из (5.6) следует пропорциональность их координат:

EMBED Equation.3

Пример 6.1. Будут ли коллинеарны векторы EMBED Equation.3 , EMBED Equation.3 ?

Решение. Координаты векторов пропорциональны, следовательно, векторы коллинеарны, причем EMBED Equation.3 .

Пример 6.2. Даны векторы

EMBED Equation.3 . Коллинеарны ли векторы EMBED Equation.3 и EMBED Equation.3 ?

Решение. Найдем координаты векторов

EMBED Equation.3

EMBED Equation.3

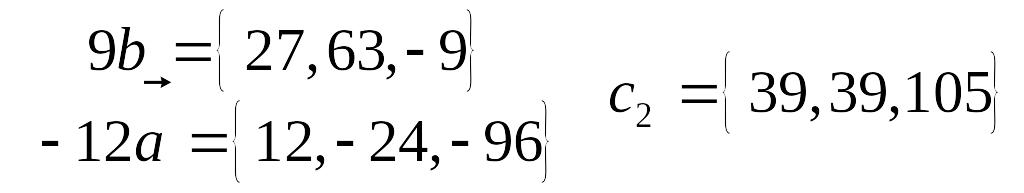
Координаты векторов не пропорциональны

EMBED Equation.3

Следовательно, векторы не коллинеарны.

6.6. Деление отрезка в данном отношении.

Даны две точки: EMBED Equation.3 и EMBED Equation.3 . На отрезке АВ найти точку EMBED Equation.3 , которая делит отрезок в отношении λ: EMBED Equation.3 . EMBED Equation.3 , т.е. EMBED Equation.3 .

Но EMBED Equation.3 и EMBED Equation.3 .

По условию коллинеарности:

EMBED Equation.3 . Отсюда EMBED Equation.3

EMBED Equation.3 (6.7)

Если λ=1, то получаем формулы деления отрезка пополам; координаты середины отрезка равны среднему арифметическому координат его концов.

EMBED Equation.3 (6.8)

Соответствующие формулы на плоскости получаются при EMBED Equation.3 из формул (6.7) и (6.8).

Пример 6.3. Даны точки А (-3, 1) и В (2, 4). В каком отношении ось Оy делит отрезок АВ?

Решение. Пусть ось Оy пересекает отрезок АВ в точке С.

Ее координаты ( 0, у). Координаты концов отрезка

EMBED Equation.3

Пример 6.4 Найти координаты центра масс треугольника АВС, если известны координаты его вершин: А (-4, -2); В (2, 0); С (1, 3).

Решение. Искомая точка лежит на пересечении его медиан. Найдем координаты точки D - середины стороны АВ:

EMBED Equation.DSMT4

Известно, что медианы треугольника пересекаются в точке М, которая делит медиану AD в отношении 1/2

EMBED Equation.DSMT4

EMBED Equation.DSMT4

Следовательно, EMBED Equation.DSMT4