8. Неопределенный интеграл и формула Ньютона - Лейбница

Теорема Коши, доказанная в предыдущем пункте, позволит получить формулу подобную формуле Ньютона – Лейбница для интегрирования функций действительного переменного, которую в дальнейшем будем называть просто формулой Ньютона – Лейбница. Значение этого очень велико, поскольку позволит перенести методы интегрирования функций действительной переменной на интегрирование функции комплексной переменной (лишь в том случае, если последние аналитические). Отметим, что если интеграл от некоторой функции по любому замкнутому контуру равен нулю, то этот интеграл не зависит от кривой интегрирования. Записывая такой интеграл, следует указывать лишь начальную и конечную точки интегрирования. Этим мы далее будем пользоваться.

Теорема 8.7. Пусть функция f(z) определена и непрерывна в некоторой односвязной области Ω, а интеграл от этой функции по любому замкнутому контуру Γ, целиком лежащему в данной области, равен нулю. Тогда функция, где, является аналитической в области Ω и первообразной к f(z).

Доказательство утверждения об аналитичности Ф(z) следует из равенства Ф'(z) = f(z), поэтому для доказательства теоремы достаточно доказать, что

. (8.1)

Левую часть равенства (8.1) преобразуем, воспользовавшись следующими двумя замечаниями.

1. Независимость интеграла от пути интегрирования (см. теорему Коши) позволяет считать, что все три точки z, z₀, z + Dz расположены на одной кривой, полностью принадлежащей области Ω. Но тогда, согласно свойству аддитивности (см. (6.3)),

.

2. Величину |Dz| мы вправе считать сколь угодно малой, так, чтобы отрезок на комплексной плоскости принадлежал области Ω. При интегрировании по прямой. Это вытекает из определения 6.1, поскольку при любом разбиении отрезка длиной Dz на части. Поэтому.

Эти два замечания позволяют левую часть равенства (8.1) представить в виде

.

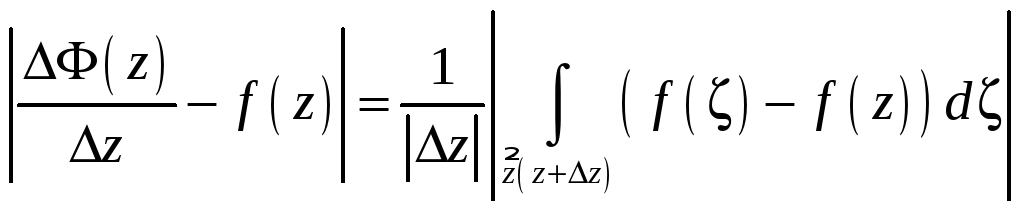Теперь, применение свойства (6.6) приводит к неравенству, из которого (8.1) следует ввиду непрерывности функции f(z) в рассматриваемой области. Доказательство закончено.

Формула Ньютона – Лейбница, справедливая для интегрирования функций действительной переменной, теперь может быть распространена на аналитические функции комплексной переменной. В самом деле, интеграл по любому замкнутому контуру, принадлежащему односвязной области аналитичности f(z) равен нулю (теорема Коши), поэтому

для любой точки z₀, принадлежащей области аналитичности f(z). Но каждый из интегралов справа представляет собой значение первообразной Ф(z) в соответствующей точке и мы получаем аналог формулы Ньютона – Лейбница

, (8.2)

где обозначено.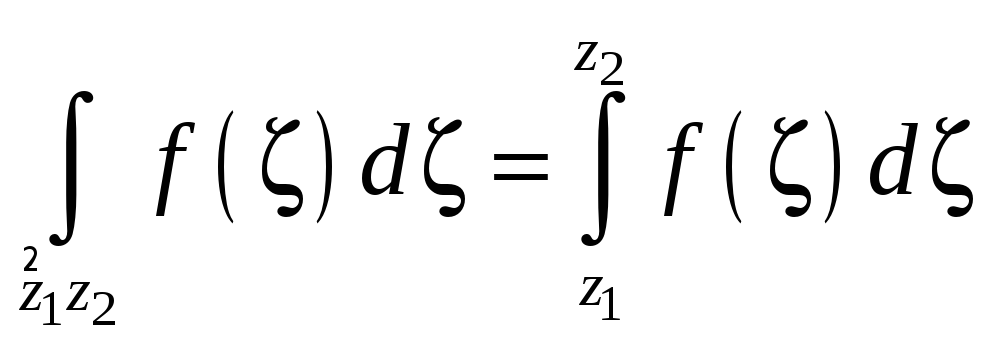

Особенности применения формулы (8.2) к функциям комплексной переменной заключаются в выполнении следующих двух требований: 1) кривая интегрирования должна находиться в односвязной области, в которой подынтегральная функция аналитична; 2) первообразная подынтегральной функции однозначна в этой области. Для демонстрации особенностей применения формулы рассмотрим (традиционный для этой темы) следующий пример.

Пусть

, (8.3)

где интегрирование может совершаться по любой линии, соединяющей точку ζ = 1 с точкой ζ = z. Очевидно, что подынтегральная функция является аналитической на плоскости  за исключением точки ζ = 0. Линия интегрирования предполагается не проходящей через начало координат.

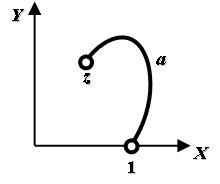
Случай 1. Найдем значение интеграла, взятого вдоль пути, не окружающего нулевую точку (см. рис. 4 ниже). Выбранную кривую можно поместить внутри односвязной области D, в которой подынтегральная функция аналитична тем самым выполнено требование 1). Для удовлетворения требования 2) нужно указать первообразную к 1/z, однозначную в этой области D. Первообразной к функции 1/z, как мы убедились ранее (см. пример 4.1), является многозначная функция (k = 0, ±1, ±2, …). Поэтому для применения формулы (8.2) необходимо выбрать какую-либо ветвь этой функции. Например, главную ветвь этой функции ln z (при k = 0). Итак, , где в качестве первообразной выбрана однозначная функция ln z (главная ветвь логарифмической функции, см.(4.7)). Так же как и для обычного криволинейного интеграла, этот результат не зависит от пути интегрирования, а только от начальной и конечной точек.

Рис. 4. Путь интегрирования в случае 1

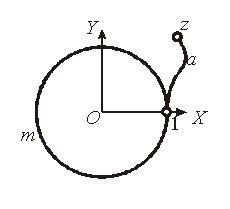
Рис. 5. Путь интегрирования в случае 2

Случай 2. Теперь в качестве пути интегрирования возьмем кривую, окружающую один раз нулевую точку так, как указано на рис. 5 по контуру.

Эту кривую нельзя поместить в односвязную область, где подынтегральная функция аналитична. Требование 1) не выполнено и нет основания для применения формулы Ньютона – Лейбница. Но интеграл вычислить можно. Для этого путь интегрирования разобьем на части и тогда.

Первое слагаемое равно 2π i (см.(4.7)), а второе слагаемое находится как в случае 1 и равно ln z. Таким образом,

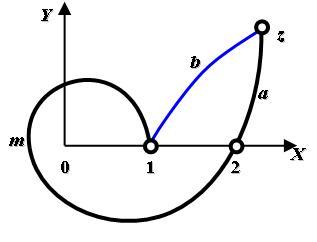
Случай 3. Путь интегрирования по кривой типа спирали 1m2az делает не меньше оборота вокруг точки z = 0 (рис 6 слева).

до деформации

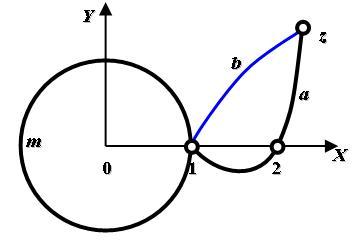
после деформации

Рис. 6. Путь интегрирования в случае 3. Деформация пути интегрирования.

Из свойств интеграла и равенства (7.3) следует, что:.

Следовательно,.

Результат вызывает недоумение, поскольку, на первый взгляд, рассмотренный случай не отличается от случая 1. Дело в том, что только первое требование применимости формулы Ньютона-Лейбница (8.2) выполнено, но не выполнено требование 2) – однозначности певообразной всюду в области интегрирования. Например, возьмем в качестве однозначной первообразной к 1/z функцию ln z (главную ветвь логарифмической функции). Если z перемещается по рассматриваемой в этом случае кривой, то аргумент переменной точки z (z – верхний предел интегрирования) двигающейся по спирали, непрерывно меняясь, увеличивается на 2 i. А теперь посмотрим, что происходит с функцией ln z = ln|z| + i arg z. Если arg z увеличился на 2 i , то мы после оборота по спирали мы приходим к функции ln|z| + i (arg z + 2) = ln z + 2 i , которая отличается от исходной на 2 i. Таким образом, первообразная к 1/z в нашей односвязной области (эту односвязную область получили с помощью соответствующего разреза) перестает быть однозначной. В данном случае для вычисления интеграла применяется следующая конструкция. Кривая интегрирования деформируется, как показано на рис.6 справа. Тогда

Случай 4. Если путь интегрирования делает n оборотов в положительном (или отрицательном) направлении около нулевой точки (по произвольной траектории), то очевидно, к значению ln z прибавляется (или отнимается) 2πn i. Следовательно (см.(3.4)). По сути, последняя формула дает интегральное представление функции Ln z и объясняет многозначность этой функции. Более того, формула показывает, каким образом возникает многозначность интеграла, понимаемого как функции верхнего предела: интеграл до некоторой степени оказывается зависящим от пути.