- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Вычисление несобственных интегралов.
Леммы Жордано широко применяются при вычислении несобственных интегралов от экспоненциально растущих функций действительной и комплексной переменной. Мы рассмотрим лишь два типа интегралов. Первые касаются несобственных интегралов от функций, не имеющих особенностей на действительной оси, а вторые имеют прямое отношение к вычислению «оригиналов» в операционном исчислении, построенном на базе преобразования Лапласа.
-
Интегралы типа
Теорема 16.19.
Пусть функция f(x), заданная на
действительной оси – ∞ < x <
∞, может быть продолжена на верхнюю
полуплоскость Im z ≥ 0
и ее аналитическое продолжение – функция
f(z) – удовлетворяет условиям
леммы Жордано в области Im z ≥ 0
и не имеет особых точек на действительной
оси. Тогда несобственный интеграл
![]() (a > 0)
существует и вычисляется по формуле
(a > 0)
существует и вычисляется по формуле
![]() , (16.4)
, (16.4)
где сумма берется по всем полюсам zk, лежащим в верхней полуплоскости.
Доказательство. Пусть число R0
таково, что все особые точки аналитического
продолжения f(z) лежат внутри
круга |z|< R0 и R >
R0. Рассмотрим замкнутый контур,
состоящий из отрезка действительной
оси R ≤ x ≤ R
и дуги полуокружности![]() .
По основной теореме о вычетах
.
По основной теореме о вычетах
![]() .
.
Здесь правая часть не зависит от R. Следовательно, при R ∞ существует предел левой части этого равенства. Переходя к пределу и воспользовавшись леммой Жордано, получим (16.4). Доказательство закончено.
Из (16.4) вытекают также следующие формулы.
![]() , (16.5)
, (16.5)
если f(x) – четная функция.
![]() , (16.6)
, (16.6)
если f(x) – нечетная функция.
Для доказательства этих равенств вначале заметим, что
![]() =
=
=![]() .
.
Отсюда равенство (16.5) следует, если предположить функцию f(x) четной, а равенство (16.6) – если предположить функцию f(x) нечетной.
Пример 16.1.
Вычислить несобственный интеграл
![]()
Решение. Чтобы воспользоваться
формулой (16.5) будем полагать a > 0,
m > 0
и проверим выполнение условий леммы
Жордано для аналитического продолжения
![]() функции
функции![]() .
В самом деле, в верхней полуплоскости
Re z ≥ 0
единственная особая точка z = i m
является простым полюсом и на действительной
оси функция f(z) не имеет особых
точек. Кроме того, на окружности |z| =
R ( R >
R0 = max(1,m)) выполняется
равномерная относительно arg z оценка
.
В самом деле, в верхней полуплоскости
Re z ≥ 0
единственная особая точка z = i m
является простым полюсом и на действительной
оси функция f(z) не имеет особых
точек. Кроме того, на окружности |z| =
R ( R >
R0 = max(1,m)) выполняется
равномерная относительно arg z оценка
![]() .
.
Таким образом, выполнены условия леммы
Жордано. По формуле (16.5) получим![]() .
.
Нетрудно заметить, что по соображениям симметрии
![]() .
.
-
Контур Бромвича и интеграл Бромвича – Вагнера.
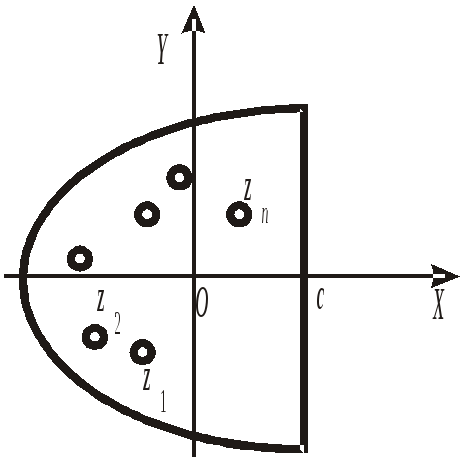
Контуром Бромвича для функции Φ(z) комплексного переменного z называется прямая (с – i ∞, с + i ∞) (замкнутая бесконечно удаленной точкой) слева от которой находятся все особые точки функции Ф(z) (рис.8). Величина с, равная расстоянию от контура Бромвича до мнимой оси 0y всегда считается неотрицательной (с ≥ 0). Если все особые точки функции Φ(z) лежат левее оси 0y, то за контур Бромвича принимается ось 0y.
|
Рис. 8. Контур Бромвича. Замыкание слева. |
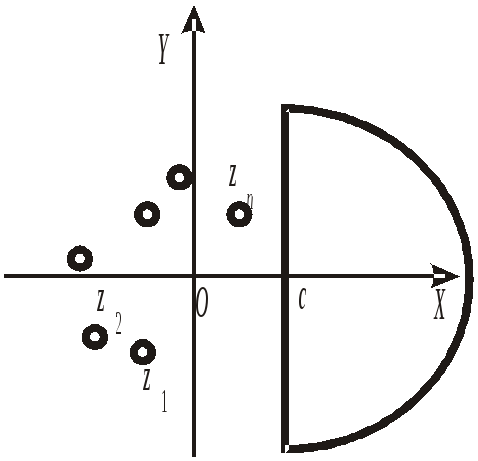
Рис. 9. Контур Бромвича. Замыкание справа
|
Пусть для функции Ф(z) прямая Re z = с: (с – i ∞, с + i ∞) является контуром Бромвича. Следующий несобственный интеграл (при t > 0)
![]() (16.7)
(16.7)
называется интегралом Бромвича – Вагнера.
Предположим, что функция Φ(z)
удовлетворяет условиям леммы Жордано
и воспользуемся леммой Жордано 16.4. Для
этого выберем достаточно большое число
R, чтобы все особые точки функции
Φ(z) оказались внутри контура,
составленного из отрезка
![]() и полуокружности CR = {|z – c| = R
, Re z < c}.
Этот контур обозначим Γ. Всюду на контуре
справедлива оценка
и полуокружности CR = {|z – c| = R
, Re z < c}.
Этот контур обозначим Γ. Всюду на контуре
справедлива оценка![]() .
Поэтому условия леммы выполняются также
и для функции
.
Поэтому условия леммы выполняются также
и для функции![]() .
Согласно основной теореме о вычетах,
имеем
.
Согласно основной теореме о вычетах,
имеем![]() .
С другой стороны,
.
С другой стороны,![]() .
Переходя к пределу при
.
Переходя к пределу при![]() ,
получим
,
получим
![]() (t > 0). (16.8)
(t > 0). (16.8)
Условие t > 0
является важным для использования
формулы (16.8). Рассмотрим, что будет, если
это условие не выполняется. Приведенная
выше оценка для функции
![]() примет вид на контуре Г
примет вид на контуре Г![]() .
Если функция Φ(z)
убывает как степенная функция, то все
несобственные интегралы расходятся и
формула (16.8) несправедлива. Однако, если
замкнуть контур Г в правой полуплоскости
(рис. 9), то для него условия леммы 16.4
выполняются и формула (16.8) примет вид
.
Если функция Φ(z)
убывает как степенная функция, то все
несобственные интегралы расходятся и
формула (16.8) несправедлива. Однако, если
замкнуть контур Г в правой полуплоскости
(рис. 9), то для него условия леммы 16.4
выполняются и формула (16.8) примет вид
![]() ,
где суммирование производится по
полюсам подынтегральной функции,
находящимся внутри контура Г. Однако,
по выбору контура Г, таких полюсов нет,
внутри контура функция является
аналитической, соответственно
,
где суммирование производится по
полюсам подынтегральной функции,
находящимся внутри контура Г. Однако,
по выбору контура Г, таких полюсов нет,
внутри контура функция является
аналитической, соответственно![]() .
Окончательно,
.
Окончательно,
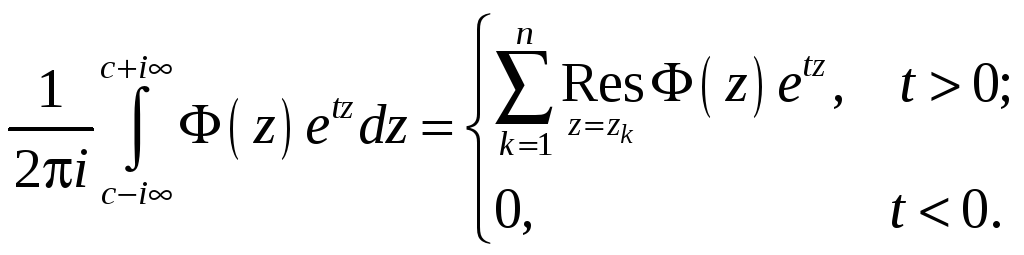 (16.9)
(16.9)
В точке t = 0 интеграл вычисляется непосредственно.