1. Расширение понятия комплексная плоскость

Введем понятие бесконечно удаленной точки комплексной плоскости, существенное для дальнейшего. Пусть дана последовательность комплексных чисел {z_n} такая, что для любого положительного числа R найдется номер N, начиная с которого члены последовательности удовлетворяют условию |z_m| > R. Такую последовательность назовем бесконечно большой. Ясно, что она не может иметь конечный предел. Такое особое положение бесконечно большой последовательности вызывает ряд неудобств. Чтобы избежать этого, введем комплексное число , и будем считать всякую бесконечно большую последовательность сходящейся к этому числу, которому поставим в соответствие бесконечно удаленную точку комплексной плоскости. Объединение комплексной плоскости  и бесконечно удаленной точки z = ∞ будем называть расширенной комплексной плоскостью и обозначать.

Отметим связь числа z = ∞ с комплексным нулем: у этих чисел не определен аргумент; если, то. В связи с этим полагают.

Для бесконечно удаленной точки устанавливаются следующие соотношения

z · ∞ = ∞ , если z  0, z + ∞ = ∞ , , если z  ∞ ,

которые естественны с точки зрения предельного перехода в операциях сложения и умножения. При этом операция является неопределенной.

2. Сфера Римана

Б.Риман предложил интерпретацию расширенной комплексной плоскости, показанную на рис.2.

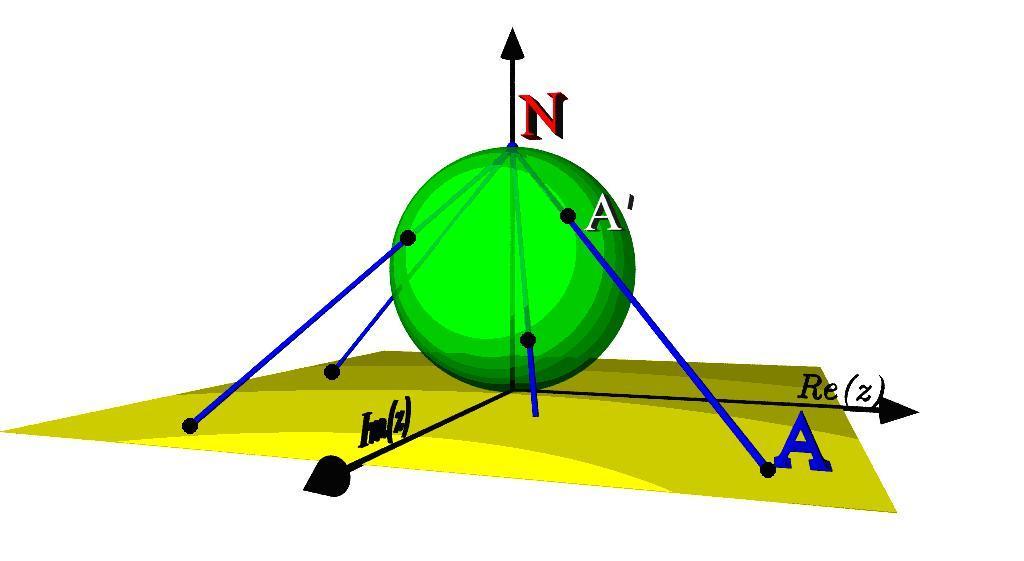
Рис. 2. Сфера Римана

Сферу, где зафиксированы северный и южный полюсы, поставим южным полюсом в начало координат. Между точками и сферы тогда устанавливается взаимно однозначное соответствие: точке A на плоскости ставится в соответствие ее проекция A на сферу из северного полюса. Ясно, что это соответствие взаимно – однозначное (изоморфизм). При этом бесконечно удаленной точке ставится в соответствие лишь одна точка – северный полюс N. Таким образом, множество точек расширенной комплексной плоскости надо трактовать как сферу Римана. Говорят изоморфно сфере Римана.

3. Функции комплексной переменной (фкп)

Рассмотрим множество. Будем говорить, что точка является внутренней точкой области, если существует  - окрестность (| z – z₀| < ) этой точки, которая принадлежит области Ω.

Точка z₀ называется граничной точкой области Ω, если любая ее  - окрестность содержит как точки принадлежащие, так и не принадлежащие области Ω.

Совокупность всех граничных точек называют границей множества  и обозначают либо гр., либо Г, либо ∂Ω. Множество, состоящее только из внутренних точек, называется открытым. Множество будем называть связным, если любые две точки области можно соединить непрерывной кривой, не выходящей за ее пределы (состоящей только из внутренних точек данного множества). Множество  называется областью, если оно открыто и связно. Область  вместе с ее границей называют замкнутой областью и обозначают, то есть,.

Пусть каждой точке z = x + iy некоторого множества Ω комплексной плоскости  поставлено в соответствие одно или несколько комплексных чисел f(z) = u + iv. Тем самым на множестве Ω определена однозначная, или соответственно, многозначная функция комплексной переменной.

f(z) = u(x,y) + iv(x,y).

Рассмотрим свойства некоторых функций.