
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Теоремы о вычетах
Теорию вычетов для вычисления контурных интегралов создал Коши в течении 1826 – 1829 годов. Основой теории являются формулы (9.1) и (9.2). Столь странное название объясняется, по-видимому, тем, что к этому понятию Коши пришел, отыскивая разность между интегралами по двум разным путям, между которыми находятся полюсы аналитической функции (то есть в результате этого вычитания и получается замкнутый контур, содержащий полюсы внутри себя). Далее, если не оговорено противное, все интегралы по замкнутому контуру берутся в положительном направлении.
Определение 12.12.
Вычетом функции f(z) в изолированной
особой точке z0 называется
число![]() .
.
Теорема 12.14. Вычет функции f(z) относительно устранимой особой точки равен нулю.
Доказательство. Устраняя особенность,
рассмотрим функцию ,
которая, как уже отмечалось, является
аналитической. Поэтому
,
которая, как уже отмечалось, является
аналитической. Поэтому![]() .
Но на контуре интегрирования f(z) = φ(z),
откуда следует утверждение теоремы.
.
Но на контуре интегрирования f(z) = φ(z),
откуда следует утверждение теоремы.
Теорема 12.15. Вычет функции f(z) относительно полюса порядка n определяется по формуле
![]() . (12.1)
. (12.1)
В частности при n = 1 (простой полюс)
![]() . (12.2)
. (12.2)
Если же при этом функцию f(z)
можно представить в виде дроби
![]() со знаменателем ψ(z0) = 0,
ψ'(z0) ≠ 0 и
со знаменателем ψ(z0) = 0,
ψ'(z0) ≠ 0 и![]() ,
то
,
то
![]() . (12.3)
. (12.3)
Доказательство. Формула (12.2) следует
из (12.1) при n = 1. Формула (12.3) с
очевидностью следует из (12.2) ввиду того,
что![]() ,
поскольку ψ(z0) = 0. Докажем
(12.1). Имеем
,
поскольку ψ(z0) = 0. Докажем
(12.1). Имеем
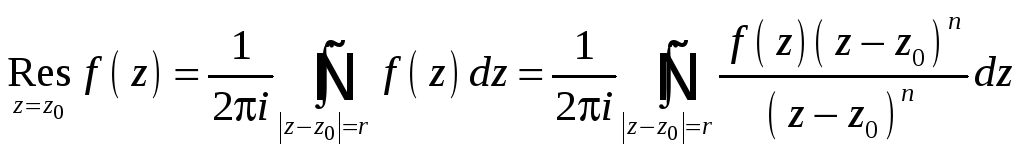 .
.
Числитель получившейся дроби имеет конечный предел при z z0 (см. определение «полюса порядка n»). Следовательно, исходя из возможности аналитического доопределения функции, бесконечной дифференцируемости аналитических функций (свойство 6 аналитических функций) и формулы (9.2), применяемой к функции (z – z0)n f(z), получим утверждение (12.1).
Теорема 12.16
(основная теорема о вычетах). Пусть
функция f(z) аналитическая в
замкнутой области
![]() за исключением конечного числа
изолированных особых точек zk Ω,
k = 1,2, … n. Тогда
за исключением конечного числа
изолированных особых точек zk Ω,
k = 1,2, … n. Тогда
![]() . (12.4)
. (12.4)
Доказательство. Каждую из особых точек
вырежем из области Ω вместе с круговыми
окрестностями |z – zk| < rk
достаточно малых радиусов rk,
чтобы была возможность применить теорему
Коши для многосвязной области. Тогда
равенство (7.2) дает![]() ,
где каждый из интегралов справа есть
соответствующий вычет, умноженный на
2π i. Доказательство
закончено.
,
где каждый из интегралов справа есть
соответствующий вычет, умноженный на
2π i. Доказательство
закончено.
-
Об аналитическом продолжении
Мы уже отметили ряд необычных свойств аналитических функций. Для обоснования возможности применения теории вычетов при интегрировании функций действительной переменной нам понадобится еще одно важное свойство – единственности аналитических функций. Это свойство позволяет заключить, что для определения функции, аналитической в данной области, достаточно знать значения этой функции на произвольном множестве из этой области, имеющем точку сгущения. А именно, справедливо следующее утверждение.
Теорема 13.17 (единственности). Пусть функция f(z) является аналитической в области Ω и обращается в нуль в различных точках zn Ω, n = 1,2,3, …. Если последовательность {zn} сходится к пределу, принадлежащему той же области Ω, то функция f(z) тождественно равна нулю в области Ω.
Доказательство. Пусть![]() .
Аналитическая функция f(z) в
окрестности этой точки представляется
степенным рядом (с радиусом сходимости
не меньше расстояния от точки z0
до границы области аналитичности функции
f(z)).
.
Аналитическая функция f(z) в
окрестности этой точки представляется
степенным рядом (с радиусом сходимости
не меньше расстояния от точки z0
до границы области аналитичности функции
f(z)).
![]() , (13.1)
, (13.1)
Поскольку f(z0) = 0, то
c0 = 0 и разложение в
окрестности z = z0
имеет вид f(z) = (z – z0)
f1(z), где![]() .
Так как f(zn) = 0 и
zn ≠ z0, то
f1(zn) = 0. В
силу непрерывности
.
Так как f(zn) = 0 и
zn ≠ z0, то
f1(zn) = 0. В
силу непрерывности
![]() c1 = 0
f1(z) = (z – z0) f2(z),
где
c1 = 0
f1(z) = (z – z0) f2(z),
где![]() .
Аналогично предыдущему получим, что и
f2(z0) = 0, то есть
с2 = 0. Этот процесс можно
продолжать неограниченно, из чего
заключаем, что все коэффициенты в
разложении (13.1) равны нулю. Но это
означает, что f(z) ≡ 0 внутри
круга сходимости. Чтобы доказать, что
f(z) = 0 в произвольной точке
z1, достаточно заметить, что
путь z0z1 состоящий
из внутренних точек области аналитичности
можно покрыть конечным числом
пересекающихся кругов, каждая точка
которых оказывается точкой сгущения
множества, где f(z) = 0.
Доказательство закончено.
.
Аналогично предыдущему получим, что и
f2(z0) = 0, то есть
с2 = 0. Этот процесс можно
продолжать неограниченно, из чего
заключаем, что все коэффициенты в
разложении (13.1) равны нулю. Но это
означает, что f(z) ≡ 0 внутри
круга сходимости. Чтобы доказать, что
f(z) = 0 в произвольной точке
z1, достаточно заметить, что
путь z0z1 состоящий
из внутренних точек области аналитичности
можно покрыть конечным числом
пересекающихся кругов, каждая точка
которых оказывается точкой сгущения
множества, где f(z) = 0.
Доказательство закончено.
Эта теорема позволяет утверждать, что две функции аналитические в одной и той же области и совпадающие на некотором участке прямой или кривой совпадают. Например, элементарные функции комплексной переменной, совпадающие на действительной оси с соответствующими функциями действительной переменной – единственные, обладающие этим свойством. Более того, из теоремы единственности вытекает, что если на отрезке [a,b] действительной оси задана непрерывная функция f(x), то в некоторой области Ω комплексной переменной, содержащий этот отрезок существует только одна аналитическая функция f(z) комплексной переменной z, принимающая данные значения f(x) на отрезке [a,b]. Функция f(z) называется аналитическим продолжением функции f(x) действительной переменной x в комплексную область Ω.
