
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Функция Хевисайда и ее интегральные представления
Пользуясь формулой (16.9) можно вычислять определенные классы несобственных интегралов. Как следует из формулы, результатом вычисления будут разрывные функции переменной t. В частности, простейшей из разрывных функций является «единичная ступенька» Хевисайда. Прежде чем определить эту функцию рассмотрим пример.
Пример 16.1.
Вычислить интеграл![]() .
.
Решение. Функция 1/z2 имеет особенность в точке z = 0 (полюс второго порядка), которая расположена слева от прямой Im z = c при c > 0. Поэтому прямая интегрирования Im z = c при c > 0 является контуром Бромвича для функции 1/z2. Следовательно, применима формула (16.8). Имеем при t > 0
![]()
По формуле (16.9) получим
![]()
При t = 0 интеграл вычислен в смысле главного значения.
Опираясь на пример, можно легко получить общую формулу для степенных функций (n ≥ 2)
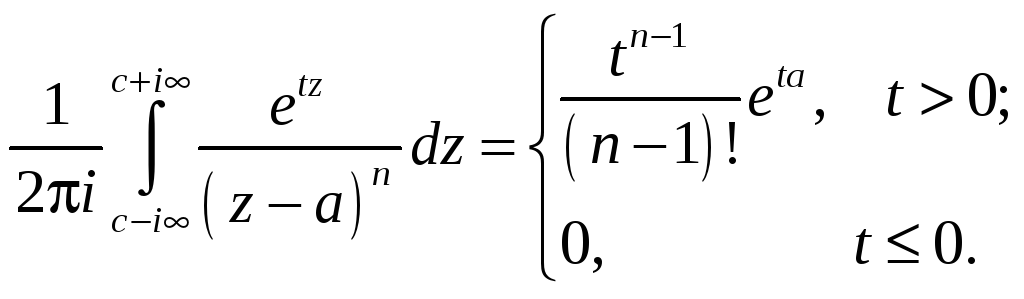 (16.10)
(16.10)
Очень важен случай n = 1. Положим для простоты a = 0:
![]() .
(16.11)
.
(16.11)
Формулу (16.9) можно применить и в данном случае. При t = 0 получим
![]() .
.
Окончательно,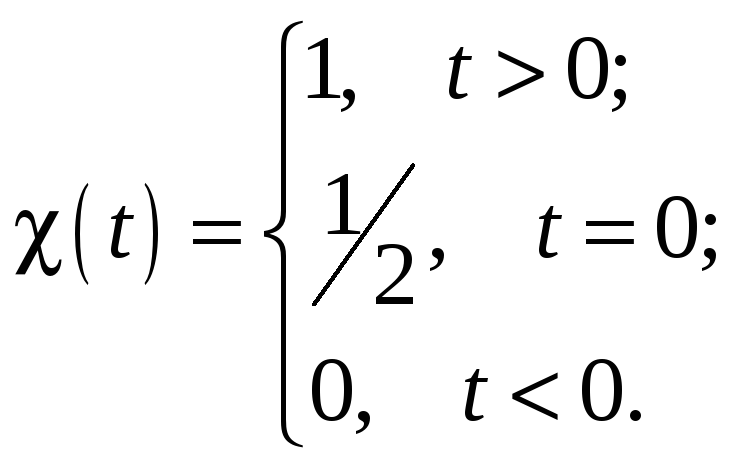 (16.12)
(16.12)
Функция (t) называется единичной ступенькой или функцией Хевисайда. Формула (16.11) является интегральным представлением функции Хевисайда.
Рассмотрим другое представление функции
Хевисайда. С этой целью вычислим интеграл
![]() (интеграл вычисляется в смысле главного
значения,
(интеграл вычисляется в смысле главного
значения,![]() ).
Если воспользуемся преобразованием
(16.4), получим представление функции:
).
Если воспользуемся преобразованием
(16.4), получим представление функции:
при a > 0
![]() ,
,
при a < 0
![]() .
.
при a = 0
![]() .
.
Разбивая область интегрирования в точке
x = 0,
преобразуем интеграл к виду![]() .
Заметим, что интеграл нечетен относительно
параметра a:
.
Заметим, что интеграл нечетен относительно
параметра a:![]() .
.
Часть 2. Решение задач по теории функций комплексной переменной
При составлении задач авторы, помимо оригинальных вариантов, руководствовались учебными изданиями [6, 7, 8]. Студентам, желающим углубить свои познания в области теории функций комплексной переменной, рекомендуются указанные книги.
-
Комплексные числа
-
Формы записи комплексных чисел
-
Комплексными числами называются
числа вида![]() ,
где
,
где
![]() и
и
![]() – действительные числа, мнимая единица
– действительные числа, мнимая единица
![]() определена равенством
определена равенством![]() .
Число
.
Число
![]() называется действительной частью
комплексного числа
называется действительной частью
комплексного числа
![]() и обозначается
и обозначается![]() ,
а число
,
а число![]() –
мнимой частью комплексного числа
–
мнимой частью комплексного числа
![]() и обозначается
и обозначается![]() .
.
Комплексное число
![]() изображается на плоскости
изображается на плоскости
![]() декартовых координат (которая в этом
случае называется комплексной плоскостью,
а оси
декартовых координат (которая в этом
случае называется комплексной плоскостью,
а оси
![]() и
и
![]() - вещественной и мнимой соответственно)
точкой с координатами
- вещественной и мнимой соответственно)
точкой с координатами
![]() или вектором, начало которого находится
в точке О(0,0), а конец в точке
или вектором, начало которого находится
в точке О(0,0), а конец в точке![]() .
.
Комплексные числа
![]() и
и
![]() равны, если равны их действительные и
мнимые части:
равны, если равны их действительные и
мнимые части:![]() ,
,![]() .
Комплексные числа
.
Комплексные числа
![]() и
и
![]() называются комплексно сопряженными
числами.
называются комплексно сопряженными
числами.
1. Алгебраическая форма:![]() .
Это основная форма записи комплексных
чисел, она представляется наиболее
естественной, поскольку в таком виде
находятся решения квадратных уравнений
(с отрицательным дискриминантом), кроме
того, именно в этой форме алгебраические
операции (сложения, умножения и др.) над
комплексными числами являются естественным
распространением известных операций
над двучленами.
.
Это основная форма записи комплексных
чисел, она представляется наиболее
естественной, поскольку в таком виде
находятся решения квадратных уравнений
(с отрицательным дискриминантом), кроме
того, именно в этой форме алгебраические
операции (сложения, умножения и др.) над
комплексными числами являются естественным
распространением известных операций
над двучленами.
2. Тригонометрическая форма:![]() ,
где
,
где
![]() - модуль числа
- модуль числа![]() ,
,
![]()
![]() - бесконечнозначный аргумент числа
- бесконечнозначный аргумент числа![]() .
Из множества значений аргумента
выделяется одно, лежащее в полуинтервале
.
Из множества значений аргумента
выделяется одно, лежащее в полуинтервале![]() ,
обозначаемое символом
,
обозначаемое символом
![]() и называемое главным значением
аргумента. Далее, если не оговорено,
для главного значения аргумента
комплексного числа
и называемое главным значением
аргумента. Далее, если не оговорено,
для главного значения аргумента
комплексного числа
![]() используется обозначение
используется обозначение![]() .
В следующей таблице приведены формулы
вычисления аргумента для различных
областей комплексной плоскости.
.
В следующей таблице приведены формулы
вычисления аргумента для различных
областей комплексной плоскости.
Таблица 1. Значения аргумента комплексного числа z
|
Область значений z |
I, IV квадрант |
II квадрант |
III квадрант |
|
x < 0, y = 0 |
|
Значение аргумента |
|
|
|
|
π |
Для комплексного числа
![]() понятие аргумента не определено.
понятие аргумента не определено.
3. Показательная форма:![]() .
.
Связь между показательной и тригонометрической формами комплексного числа осуществляется формулой Эйлера:
![]()
