
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Аналитические функции
Определение 5.7. Функция f(z) называется аналитической в точке, если она дифференцируема в некоторой окрестности этой точки.
Определение 5.8. Функция f(z) называется аналитической в области Ω, если она дифференцируема в каждой ее точке, а ее производная непрерывна в этой области.
Замечание. Условие непрерывности производной аналитической функции в дальнейшем можно будет снять, поскольку аналитическая функция комплексной переменной оказывается бесконечно дифференцируемой (см. ниже свойство 5.6).
Из теоремы 4.1 и из условий дифференцируемости функций двух переменных вытекает следующий критерий аналитичности: Для аналитичности функции f(z) = u(x,y) + i v(x,y) в области Ω необходимо и достаточно, чтобы в этой области существовали непрерывные частные производные функций u(x,y) и v(x,y), удовлетворяющие условиям Коши – Римана (4.1).
-
Свойства аналитических функций
Ряд свойств дифференцируемых функций действительного переменного легко переносится на аналитические функции из - за идентичности определения производных. Но имеются и ряд специфических свойств (см. далее свойства 3,4,5).
Свойство 5.1. (об арифметических
действиях над аналитическими функциями).
Если f1(z) и f2(z)
аналитические в области Ω, то их сумма,
разность, и произведение являются
аналитическими функциями. Функция
![]() является аналитической всюду в области
Ω, где f2(z)
0.
является аналитической всюду в области
Ω, где f2(z)
0.
Свойство 5.2. (об аналитичности суперпозиции). Если w = f(z) аналитическая функция в области Ω(z) комплексной плоскости, а в области ее значений Ω(w) определена аналитическая функция = (w), то функция F(z) = (f(z)), является аналитической в области Ω(z).
Свойство 5.3. (об аналитичности
обратной функции). Пусть w = f(z)
аналитическая функция в области Ω(z),
причем![]() .
Тогда в области ее значений Ω(w)
определена обратная функция z = f – 1(w),
являющаяся аналитической функцией в
области Ω(w) и имеет место равенство
.
Тогда в области ее значений Ω(w)
определена обратная функция z = f – 1(w),
являющаяся аналитической функцией в
области Ω(w) и имеет место равенство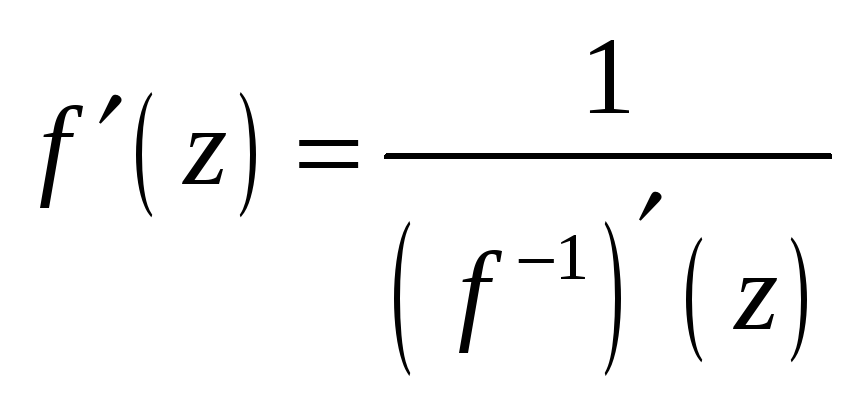 .
.
С
Рис. 3. Пути интегрирования при вычислении
криволинейного интеграла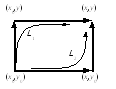
Доказательство. Пусть, например, известна
действительная часть u(x,y)
аналитической функции f(z) = u(x,y) + i v(x,y).
Условия Коши – Римана (5.1) позволяют
найти полный дифференциал неизвестной
мнимой части:
![]() .
Остается воспользоваться правилом
восстановления функции по ее полному
дифференциалу
.
Остается воспользоваться правилом
восстановления функции по ее полному
дифференциалу
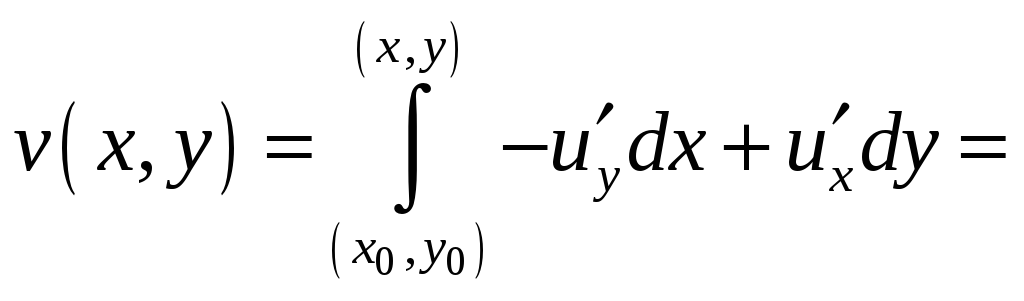
![]() ,
,
которое определит функцию v(x,y)
c точностью до константы. При вычислении
криволинейного интеграла, учитывая,
что подынтегральное выражение является
полным дифференциалом и не зависит от
пути интегрирования, выбран путь L1
, показанный на рис.3. Аналогично можно
получить формулу для восстановления
действительной части аналитической
функции:
![]()
Доказательство закончено.
Определение 5.9. Две линии называются ортогональными в точке пересечения, если ортогональны их касательные в этой точке.
Свойство 5.5. Пусть f(z) = u(x,y) + i v(x,y) аналитическая функция в области Ω. Семейства линий уровня действительной и мнимой части u(x,y) = C1, v(x,y) = C2 взаимно ортогональны:
(grad u, grad v) = 0.
Доказательство вытекает из условий Коши - Римана (5.1):
![]()
Свойство 5.6. Функция f(z), аналитическая в области Ω имеет в каждой точке этой области производные любого порядка.
Доказательство, основанное на представлении аналитических функций рядами Тейлора, мы опускаем. Отметим в этой связи, что возможность представления функции степенным рядом равносильна аналитичности и во многих учебниках такие функции по определению называются аналитическими (см, например книги [3, 4, 5]). Отметим также, что существование производных любого порядка от аналитической функции вытекает из формулы Коши, которая будет доказана в дальнейшем.
