
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Примеры с решениями
В примерах 5.6 – 5.8 вычислить контурные интегралы.
Пример 5.6.
![]()
Решение. Согласно основной теореме о вычетах запишем
![]() .
.
Полюсы подынтегральной функции
![]() и
и
![]() простые, поэтому можем воспользоваться
формулой (5.5). В результате
простые, поэтому можем воспользоваться
формулой (5.5). В результате
![]()
Пример 5.7.![]() ,
где
,
где
![]() – эллипс
– эллипс
![]()
Решение. Точки
![]() , и
, и
![]() есть полюсы второго порядка подынтегральной
функции
есть полюсы второго порядка подынтегральной
функции![]() ,
причем
,
причем
![]()
Найдем вычеты в этих точках. Имеем

![]() ;
;
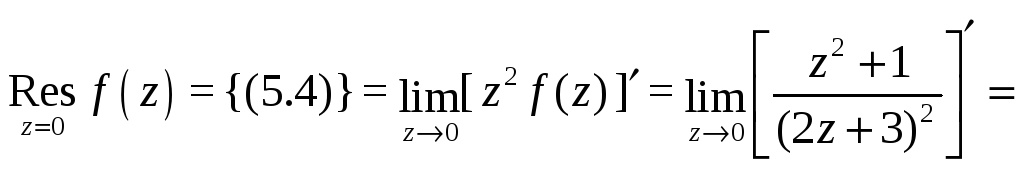
![]()
По основной теореме о вычетах
![]()
Пример 5.8.
Вычислить интеграл .
.
Решение. Точки
![]() и
и
![]() являются полюсами 2-го порядка, но точка
являются полюсами 2-го порядка, но точка
![]() лежит вне окружности
лежит вне окружности![]() ,
а потому
,
а потому
Рис. 14. График к примеру 5.8.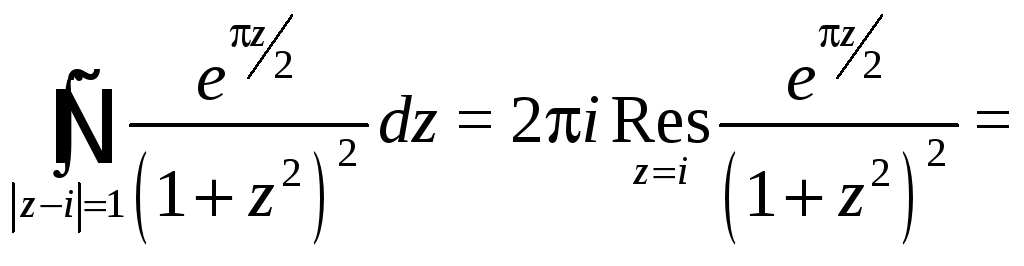

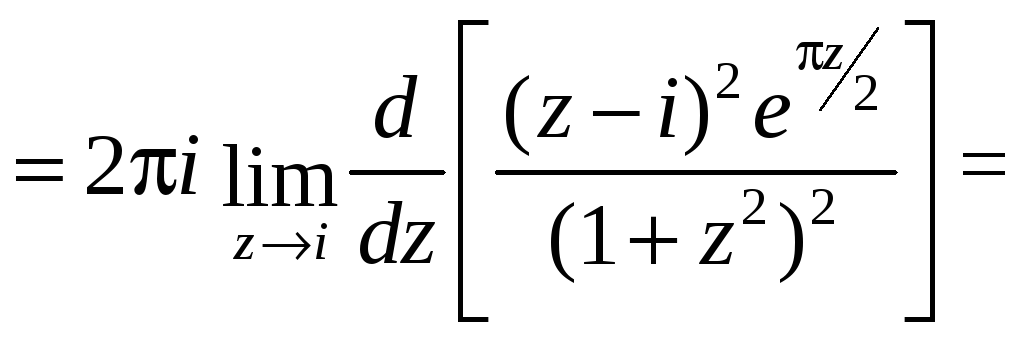
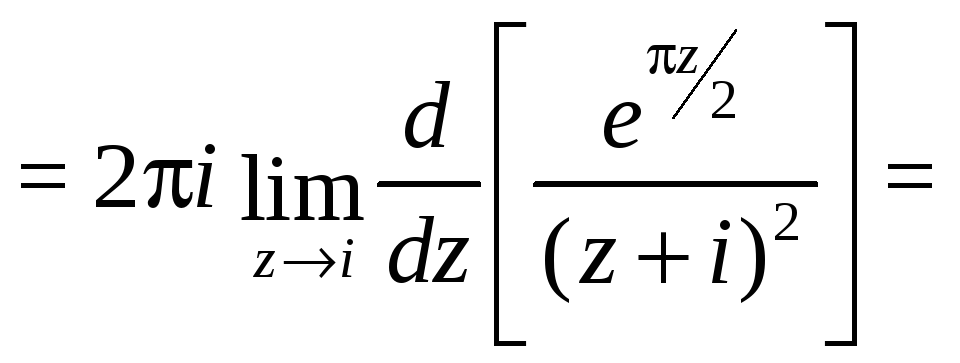
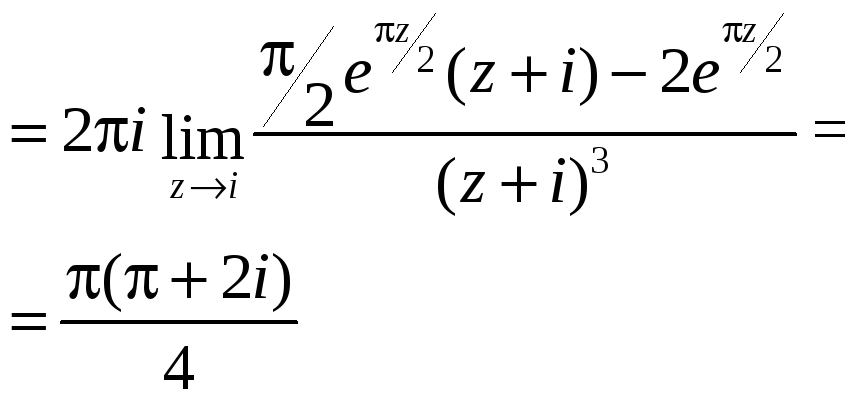
-
Задачи для самостоятельного решения
1. Найти изолированные особые точки и определить их тип.
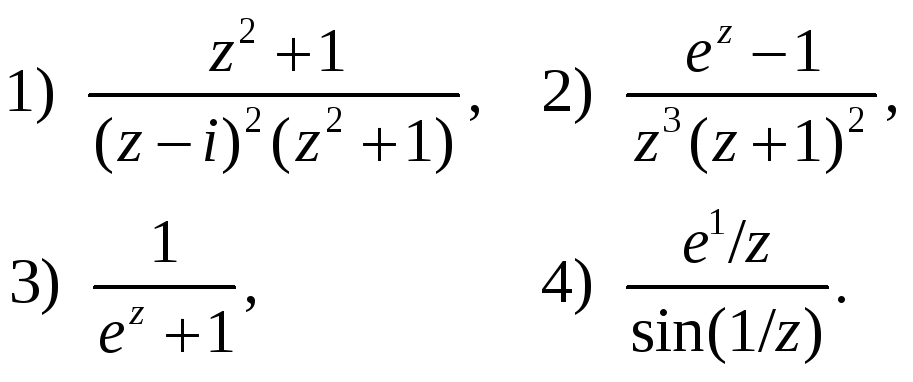
2. Найти вычеты в конечных особых точках функции:
![]()
![]()
3. Вычислить контурные интегралы.
1)![]() 2)
2)
![]()
3)![]() 4)
4)
![]()
5)![]() 6)
6)
![]()
7)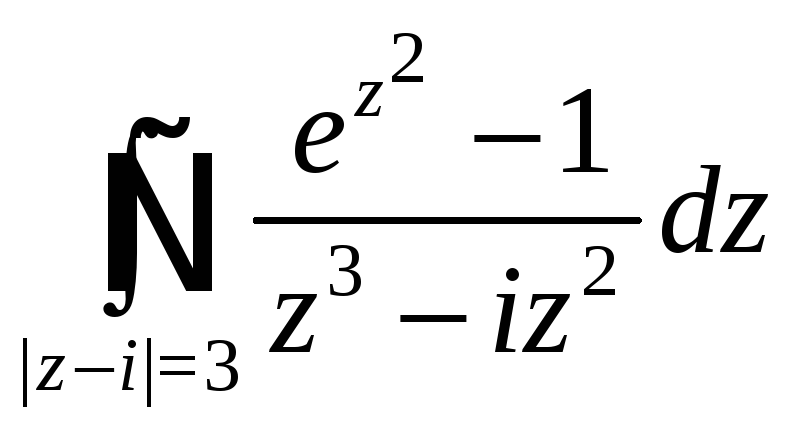 8)
8)
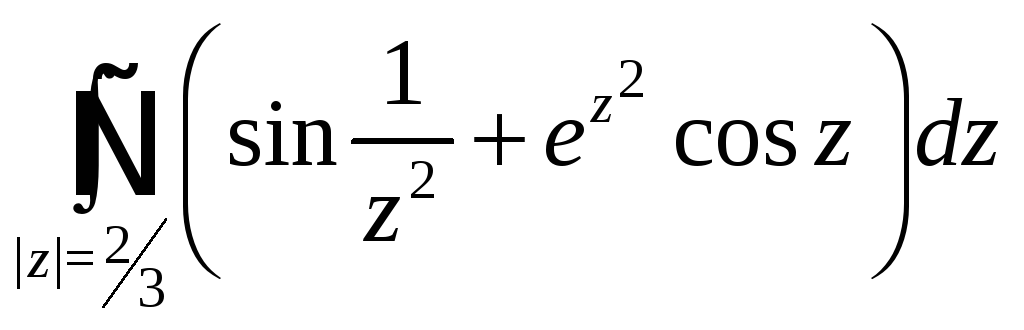
9)![]() ,
где
,
где
![]()
-
Вычисление определенных интегралов от действительных функций
-
Интегралы типа
-
Пример 6.1
![]()
Решение. Введем переменную![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
и при изменении
,
и при изменении
![]() от 0 до
от 0 до
![]() переменная
переменная
![]() пробегает один раз окружность
пробегает один раз окружность
![]() в положительном направлении.
в положительном направлении.
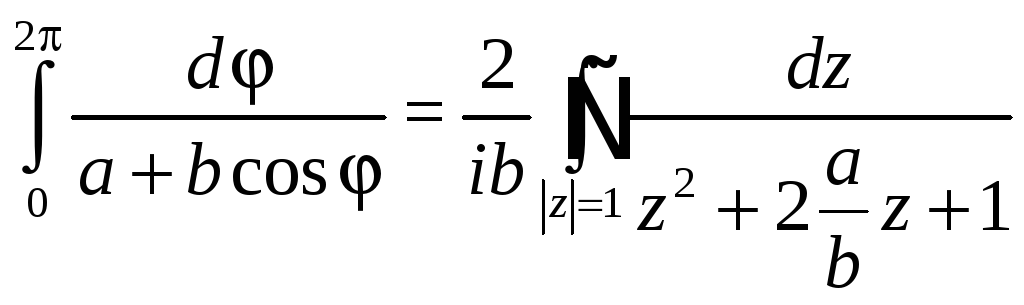 .
.
Подынтегральная функция имеет две
особые точки![]() ,
которые являются полюсами 1-го порядка,
причем внутри контура
,
которые являются полюсами 1-го порядка,
причем внутри контура
![]() лежит только точка
лежит только точка![]() .
По основной теореме о вычетах имеем
.
По основной теореме о вычетах имеем
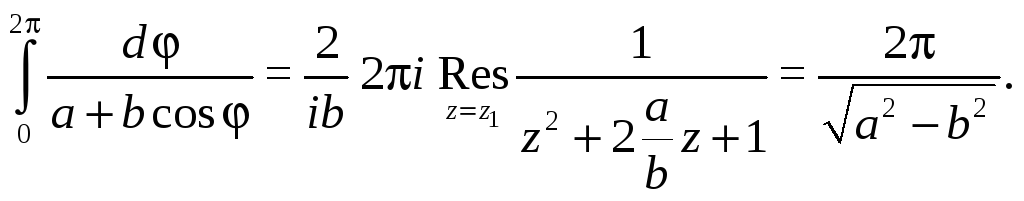
Пример 6.2.
Показать, что интеграл
![]() для любой непрерывной функции f(x)
равен 0, если
для любой непрерывной функции f(x)
равен 0, если![]() .
.
Решение. Пользуясь периодичностью тригонометрических функций, получим
![]() ,
,
так как интеграл от нечетной функции в симметричных пределах равен нулю.
Пример 6.3.
Вычислить интеграл![]() .
.
Решение. Воспользовавшись результатами
примера 6.1, получим:
![]()
-
Вычисление несобственных интегралов второго рода
Формула для вычислений и условия для ее применения даются в теореме 15.1 лекций:
![]()
![]()
Пример 6.3.
![]()
Решение. Аналитическое продолжение
подынтегральной функции
![]() имеет в верхней полуплоскости
имеет в верхней полуплоскости
![]() две особые точки
две особые точки
![]() и
и![]() ,
которые являются полюсами первого
порядка. Используя формулу (6.1), получаем
,
которые являются полюсами первого
порядка. Используя формулу (6.1), получаем
![]()
![]()
-
Вычисление интегралов вида
Сразу же отметим, что методика вычисления
интегралов указанного вида применяется
при нахождении интегральных преобразований
Фурье (![]() )
и Лапласа (
)
и Лапласа (![]() )
функции
)
функции![]() .
Мы рассмотрим указанные интегралы
только для
.
Мы рассмотрим указанные интегралы
только для![]() .
.
Формулы для вычислений и условия применения даются в теоремах раздела 16 лекций. При указанных в этом разделе условиях
![]() .
. ![]()
Из (6.2), учитывая, что![]() ,
,
![]() ,
вытекают формулы
,
вытекают формулы
![]() ,
, ![]()
![]() .
. ![]()
Пример 6.5.
Вычислить интеграл
![]()
Решение. Нетрудно видеть, что
аналитическое продолжение
![]() удовлетворяет всем условиям теоремы
16.1 лекций, а в верхней полуплоскости
удовлетворяет всем условиям теоремы
16.1 лекций, а в верхней полуплоскости
![]() находится одна особая точка
находится одна особая точка
![]() – простой полюс. Применяя формулу (6.3),
получим
– простой полюс. Применяя формулу (6.3),
получим
![]()
![]() .
.
Пример 6.6.
Вычислить интеграл![]() .
.
Решение. В данном случае, прежде воспользуемся четностью подынтегральной функции, а затем применим формулу (6.4). Получим
![]()
![]() .
.
Пример 6.7.
Вычислить интеграл
![]() полагая
полагая
![]() ,
,
![]() .
.
Решение. Вначале вычислим
вспомогательный интеграл
![]() по контуру C, показанному
на рис. 15. По теореме Коши 7.1
по контуру C, показанному
на рис. 15. По теореме Коши 7.1
![]() ,
так как подынтегральная функция является
аналитической всюду в области
интегрирования, ограниченной контуром
C.
,
так как подынтегральная функция является
аналитической всюду в области
интегрирования, ограниченной контуром
C.
Поэтому
Рис. 15. Контур к примеру 6.7![]()
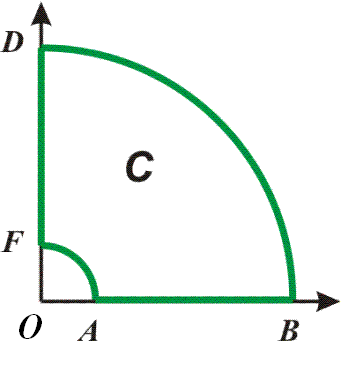 .
.
Полагая
![]() ,
для интегралов, входящих в сумму, получим
,
для интегралов, входящих в сумму, получим
1)
![]() по лемме Жордано 16.1;
по лемме Жордано 16.1;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
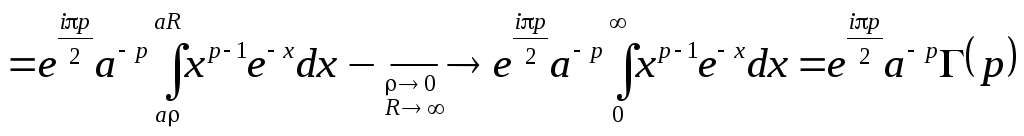 ,
,
где
![]() гамма-функция
(табулированная специальная функция).
Окончательно
гамма-функция
(табулированная специальная функция).
Окончательно
![]() .
Выделяя действительную и мнимую части
последней формулы, имеем
.
Выделяя действительную и мнимую части
последней формулы, имеем
![]() ,
,
![]()
