1. Различные формы представления комплексных чисел

1

Рис. 1. Число на комплексной плоскости.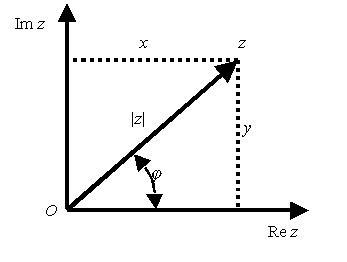

. Алгебраическая форма. Это основная форма представления уже упоминавшаяся выше: z = x + iy, x и y – действительные числа. Число x = Re z называется действительной частью комплексного числа z, а число y = Im z – мнимой.

Геометрическое представление показано на рис.1: точка z c координатами (x, y) на плоскости в прямоугольной системе координат xOy (комплексная плоскость, обозначается тем же символом, что и множество комплексных чисел ). Число z можно отождествить и с вектором (x,y) начало которого совпадает с точкой О. При такой интерпретации сложение и вычитание комплексных чисел производится по правилам сложения и вычитания векторов.

2. Тригонометрическая форма. Пусть  – угол между вектором Oz и осью Ox. Тогда из геометрического представления комплексного числа z вытекает, что. Имеем z = x + iy =  = , где |z| – модуль числа z, а угол  – аргумент этого комплексного числа. Это представление не единственно, что связано с периодичностью тригонометрических функций.

Принято обозначать

,

В дальнейшем, если не оговорено особо, под  подразумеваем главное значение аргумента из полуинтервала.

3. Показательная форма. Из доказанной в теории рядов формулы Эйлера следует

Интересно отметить неожиданную связь, которую открыла показательная форма комплексного числа между числами e,  и i, которые появились в математике по совершенно разным причинам: число e - как основание натурального логарифма ,  - как отношение длины окружности к ее диаметру, а мнимая единица i введена для определения решения любого квадратного уравнения. Полагая z = – 1, мы получим, что.

Приведенные формы представления комплексных чисел используются в различных случаях. Например, из геометрического представления следуют неравенства треугольника (очевидные для векторов)

. (1.1)

Из тригонометрического представления следуют формулы для умножения комплексных чисел в тригонометрической и показательной формах

,

возведения в степень и извлечения корней.

Формула возведения в степень обычно называется формулой Муавра. Последняя формула дает n различных корней (при k = 0, 1, 2, … , n – 1) из комплексного числа z. Например, уравнение z⁴ + 1 = 0 имеет 4 различных корня:

.

В связи с этим примером уместно вспомнить о заблуждении Лейбница (см. Введение). На самом деле мы имеем тождество

,

из которого вытекает так и не полученное Лейбницем разложение на квадратные многочлены с действительными коэффициентами, поскольку

.

2. Предел последовательности комплексных чисел

Дадим два равносильных определения последовательности комплексных чисел.

Определение 2.1. Комплекснозначная функция натурального аргумента называется последовательностью комплексных чисел.

Определение 2.2. Последовательностью комплексных чисел называется перенумерованное бесконечное множество комплексных чисел. Обозначение: {z_n} , n = 0, 1, 2, …

Определение 2.3. Число z = a + ib называется пределом последовательности {z_n} если для любого положительного числа  можно указать такой номер N(), начиная с которого все элементы z_n этой последовательности удовлетворяют неравенству |z – z_n| < , при n > N(). Обозначение:.

Поскольку каждое комплексное число z_n = a_n + ib_n характеризуется парой действительных чисел a_n и b_n, то последовательности комплексных чисел соответствуют две последовательности действительных чисел {a_n} и {b_n}. При этом очевидны соотношения |a_n – a|  |z_n – z|, |b_n – b|  |z_n – z|,

,

из которых вытекают следующие три утверждения, хорошо известные для последовательностей действительных чисел.

Теорема 2.1. Последовательность {z_n} имеет предел тогда и только тогда, когда имеют пределы последовательности действительных {a_n} и мнимых {b_n} частей последовательности {z_n}.

Теорема 2.2. Из всякой ограниченной последовательности {z_n} (т.е. |z_n|  M, n = 0, 1, 2, …) можно выделить сходящуюся подпоследовательность.

Критерий Коши. Последовательность {z_n} сходится тогда и только тогда, если для любого  > 0 можно указать такое число N(), что |z_n – z_n + m| <  для любых n  N(),.