6. Интеграл по комплексной переменной.

   1. Основные свойства.

Пусть в области определения функции f(z) = u(x,y) + i v(x,y) заданы две точки и кривая их соединяющая. Для определения интеграла от функции комплексного переменного воспользуемся схемой определения криволинейного (второго рода) от функций действительного переменного.

Определение 6.10. Произведем произвольное разбиение кривой на части точками. В каждой из частей произвольно выберем точку. Составим интегральную сумму , где (), и обозначим. Если существует конечный предел этой суммы при l  0, не зависящий от способа разбиения кривой на части и от выбора точек z_j, то он называется интегралом по кривой от функции комплексного переменного f(z):

.

Пусть f(z) = u(x,y) + i v(x,y). Учитывая, что Dz_j = Dx_j + i Dy_j, получим следующее представление интегральной суммы

,

из которой вытекает основная формула для вычисления интегралов от функций комплексного переменного

. (6.1)

Это равенство может служить определением интеграла от функции f(z) по кривой и дает возможность перенести основные свойства криволинейных интегралов (второго рода) от функций действительной переменной на интегралы по комплексной переменной. Перечислим эти свойства.

1) . (6.2)

2) . (6.3)

3) Если a – комплексная постоянная, то

. (6.4)

4) . (6.5)

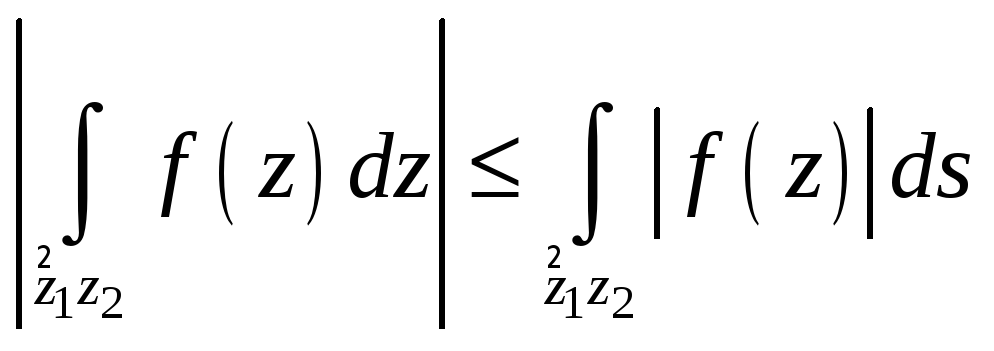5) , (6.6)

где ds – дифференциал длины дуги кривой и в правой части неравенства находится криволинейный интеграл первого рода от действительной функции.

Пятое свойство кажется необычным из-за присутствия (справа) криволинейного интеграла первого рода. Однако оно легко вытекает из неравенства треугольника:

6) Имеет место следующая формула замены переменных

, (6.7)

где z =φ (z) – аналитическая функция z, устанавливающая взаимно однозначное соответствие между кривыми С и Г.

В частности

, (6.8)

где z = z(t) (x = x(t), y = y(t)) есть комплексно - параметрическое задание кривой C, а z(α), z(β) – соответственно начальная и конечная точка последней.

7. Теорема Коши

Определение 7.11. Замкнутым контуром будем называть кусочно-гладкую замкнутую кривую, не имеющую точек самопересечения.

Область, ограниченную одним замкнутым контуром будем называть односвязной, двумя (внутренним и внешним контуром) – двухсвязной и т.д..

За положительное направление обхода контура принято считать такое, при котором внутренняя область, ограниченная данным замкнутым контуром, остается слева от направления движения. Интегрирование в отрицательном направлении будем обозначать. Нам понадобится формула Грина

, (7.1)

связывающая криволинейный интеграл второго рода по замкнутому контуру с двойным интегралом по области ограниченной этим контуром.

Теорема 7.4 (Коши) Пусть в односвязной замкнутой области задана однозначная аналитическая функция f(z). Интеграл от этой функции по любому замкнутому контуру Γ, целиком лежащим в области аналитичности равен нулю.

Доказательство. К криволинейным интегралам справа в формуле (6.1) применим формулу Грина. Получим

,

.

Теперь утверждение теоремы вытекает из условий Коши – Римана.

Приведем два обобщения этой теоремы. Первое из них позволяет применять теорему Коши, если замкнутый контур является границей области аналитичности.

Теорема 7.5 (вторая формулировка теоремы Коши). Если функция f(z) является аналитической функцией в односвязной области Ω, ограниченной кусочно-гладким контуром ∂Ω и непрерывна в замкнутой области, то.

Второе обобщение распространяет теорему Коши на многосвязные области (граница состоит из нескольких замкнутых контуров).

Теорема 7.6. Пусть f(z) является аналитической функцией в многосвязной области Ω, ограниченной извне контуром C₀, а изнутри контурами C₁, C₂, … ,C_n, и пусть f(z) непрерывна в замкнутой области. Тогда, где С – полная граница области.

Доказательство. Проведем гладкие непересекающиеся друг с другом кривые Γ₁, Γ₂, … ,Γ_n соединяющие контур C₀ с контурами внутренних границ C₁, C₂, … ,C_n. Тогда область, ограниченная кривыми C₀,C₁, C₂, … ,C_n и кривыми Γ₁, Γ₂, … ,Γ_n, проходимыми дважды в противоположных направлениях, оказывается односвязной. В силу теоремы 6.3 интеграл по границе этой области равен нулю. Но интегралы по вспомогательным кривым Γ₁, Γ₂, … , Γ_n проходятся дважды в противоположных направлениях и при суммировании друг друга уничтожают. В результате мы получим равенство

. (7.2)

Следствие. Если функция аналитична в многосвязной замкнутой области, то интеграл по внешнему контуру равен сумме интегралов по внутренним контурам (при этом все интегралы вычисляются либо в положительном направлении, либо в отрицательном).

Пример 7.1. Вычислить интеграл, где C – некоторый контур, внутри которого находится точка z = 0. По следствию контур C можно заменить окружностью |z| = r достаточно малого радиуса r, чтобы выбранная нами окружность целиком содержалась в области ограниченной исходным контуром. Имеем

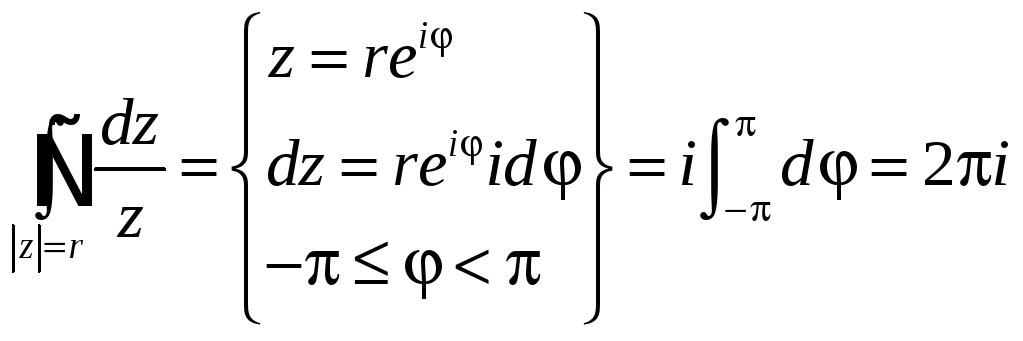. (7.3)