
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Примеры с решениями
Пример 1.1. В задачах 1 – 6 записать данные комплексные числа в тригонометрической и показательной формах.
1.
![]()
2.
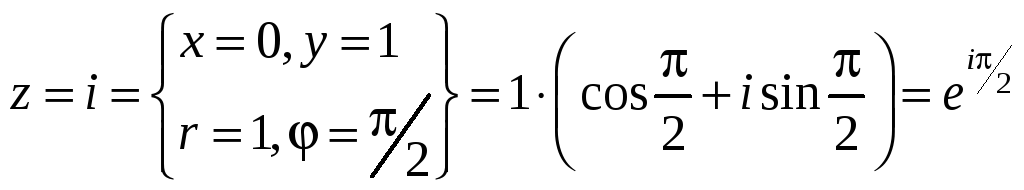
3.
![]()
4.
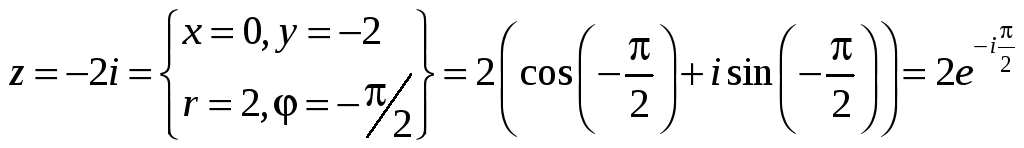
5.
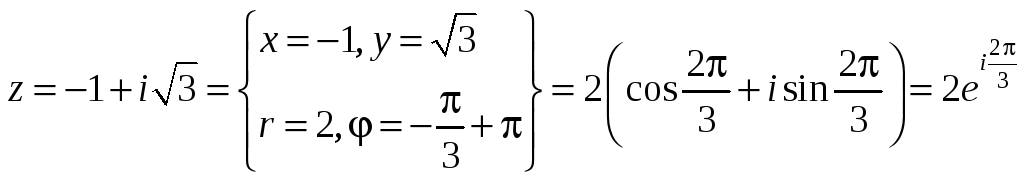
6.
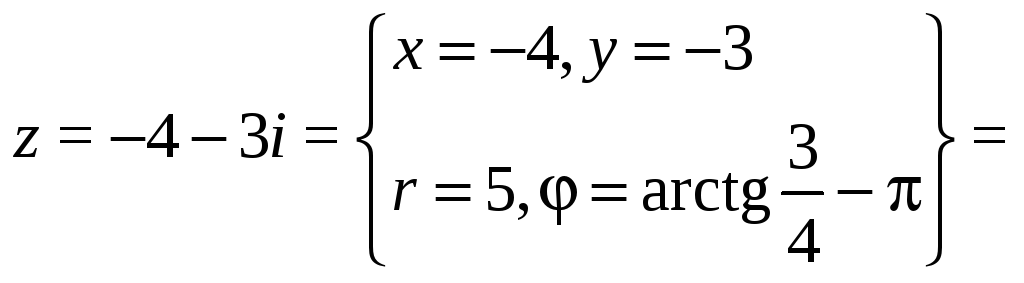
![]()
7.
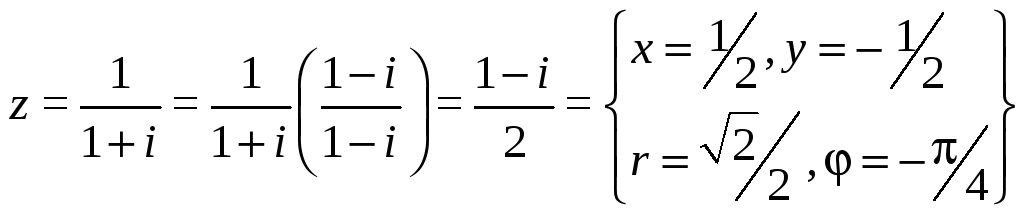 =
=
![]()
-
Алгебраические операции над комплексными числами
Алгебраические операции сложения и умножения над комплексными числами вводятся по правилам сложения и умножения двучленов, т.е., если
![]()
![]()
то
![]() ,
,
![]() .
.
Для любого комплексного числа
![]() существует обратное
существует обратное![]() ,
т.е. такое, что
,
т.е. такое, что![]() .
Легко проверить, что этим числом является
число
.
Легко проверить, что этим числом является
число
![]() ,
где
,
где
![]() – комплексно-сопряженное число.
– комплексно-сопряженное число.
Например, представим комплексное число
![]() в алгебраической форме.
в алгебраической форме.
Решение.
![]()
Умножение и деление комплексных чисел
можно производить не в алгебраической,
а в тригонометрической форме. Использование
формул тригонометрии дает следующий
результат: пусть![]() ,
,
![]() ,
,
![]() ,
,
![]() , тогда
, тогда
![]() ,
, ![]()
![]() .
. ![]()
Здесь видим простое правило: при произведении модули перемножаются, а аргументы складываются; при делении модули делятся, а аргументы вычитаются.
Целая степень комплексного числа определяется многократным умножением. При этом, возможно использование формулы бинома Ньютона, а если степень не велика, то формул сокращенного умножения, например
![]()
Для возведения комплексного числа в
степень удобно пользоваться не
алгебраической, а тригонометрической
или показательной формами записи
комплексного числа. Справедлива следующая
формула, которая носит название формула
Муавра: для
![]()
![]()
![]()
![]()
![]()
Корень
![]() -й
степени (
-й
степени (![]() )
из комплексного числа
)
из комплексного числа
![]() имеет
имеет
![]() различных значений, которые находятся
по формуле:
различных значений, которые находятся
по формуле:
![]() ,
, ![]()
где![]() .
Эти значения расположены на окружности
радиуса
.
Эти значения расположены на окружности
радиуса
![]() с центром в начале координат и делят ее
на n равных частей (т.е. при
с центром в начале координат и делят ее
на n равных частей (т.е. при
![]() являются вершинами правильного
n-угольника, вписанного в эту
окружность).
являются вершинами правильного
n-угольника, вписанного в эту
окружность).
Пример 1.2.
Найти произведение и частное чисел
![]() и
и![]() .
.
Решение. По формулам (1.1) – (1.2)
![]() ,
,
![]() .
.
Пример 1.3.
Вычислить![]() .
.
Решение. Модуль числа
![]() равен
равен![]() ,
а главное значение его аргумента
,
а главное значение его аргумента![]() .
По формуле (1.3)
.
По формуле (1.3)
![]() .
.
Пример 1.4.
Найти все значения![]() .
.
Решение. Искомые корни обозначим
![]() Модуль подкоренного числа равен 1, а
аргумент (главный) равен 0. Отсюда, по
формуле (1.5),
Модуль подкоренного числа равен 1, а
аргумент (главный) равен 0. Отсюда, по
формуле (1.5),
![]() .
.
При
![]()
![]() ,
при
,
при
![]()
![]() ,
при
,
при
![]()
![]() .
Корни уравнения показаны на рис. 10.
.
Корни уравнения показаны на рис. 10.
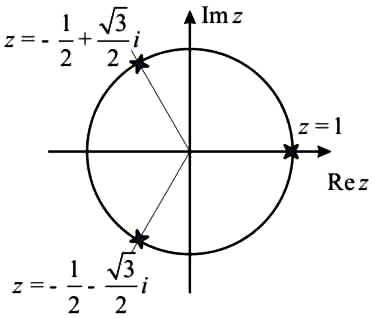
Рис. 10. Корни уравнения
![]()
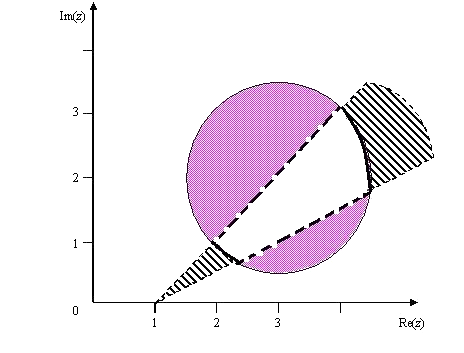
Рис. 11. Построение области к примеру 1.5.
Пример 1.5. Построить область
![]() на комплексной плоскости
на комплексной плоскости
Решение. Первая из областей (![]() )
представляет собой сектор с началом в
точке
)
представляет собой сектор с началом в
точке![]() .
Границы сектора отмечены пунктирной
линией, поскольку они заданы строгим
неравенством.
.
Границы сектора отмечены пунктирной
линией, поскольку они заданы строгим
неравенством.
Вторая область
![]() представляет собой круг с центром в
точке
представляет собой круг с центром в
точке
![]() и радиусом
и радиусом![]() .
Граница области изображена сплошной
линией, так как область задана нестрогим
неравенством. Искомая область есть
пересечение сектора и круга. На рис.11
эта область не заштрихована.
.
Граница области изображена сплошной
линией, так как область задана нестрогим
неравенством. Искомая область есть
пересечение сектора и круга. На рис.11
эта область не заштрихована.
-
Задачи для самостоятельного решения
1. Вычислить, исходя из определения
числа![]() :
:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
2. Найти действительную и мнимую части комплексных чисел и изобразить их на комплексной плоскости:
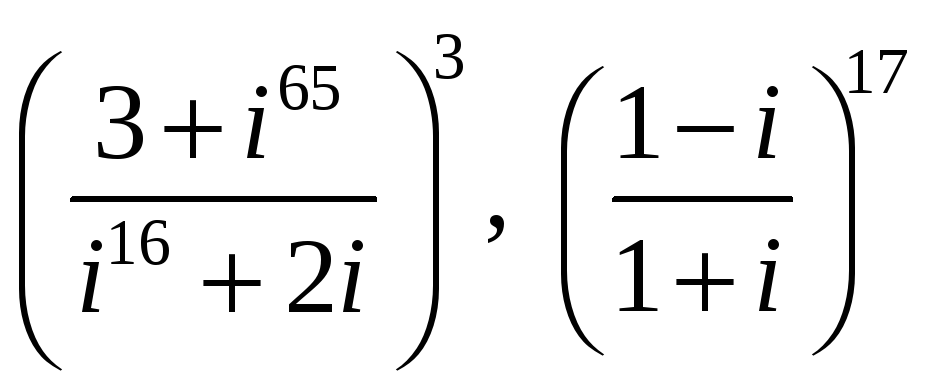
3. Найти модули и аргументы комплексных
чисел. Изобразить числа на комплексной
плоскости и записать их в тригонометрической
и показательной формах:
![]()
4. Вычислить по формуле Муавра:
![]()
5. Найти все значения корней: а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() .
.
6. Найти главное значение аргумента
комплексного числа![]() .
.
7. Все ли заданные числа записаны в
тригонометрической форме? Если нет, то
записать их в тригонометрической и
показательной формах: а)![]() ,
б)
,
б)![]() .
.
8. Представить в тригонометрической
форме число
![]() .
.
9. Числа![]() ,
,
![]() ,
,
![]() представить
в алгебраической, тригонометрической
и показательной формах.
представить
в алгебраической, тригонометрической
и показательной формах.
10. Числа![]() ,
,
![]() и
и
![]() даны в задании 9. Решить уравнения
даны в задании 9. Решить уравнения![]() .
.
11. Построить линии на комплексной
плоскости:
1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]() ,
5)
,
5)![]() .
.
12. Построить области на комплексной плоскости:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
