
- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Вычисление интегралов типа
Для вычисления интегралов указанного типа введем комплексную переменную z = ei θ. Тогда
![]() ,
,
где![]() .
.
Как видим, мы получили интеграл по замкнутому контуру от рациональной функции. Пусть знаменатель этой функции имеет n корней, среди которых m корней zk(k = 1,2, … m) лежат (строго) внутри контура |z| = 1. Тогда, согласно основной теореме о вычетах, получим ответ в виде
![]() .
.
Пример 14.1.
Вычислить интеграл![]() ,
0 < a < 1.
,
0 < a < 1.
Решение.
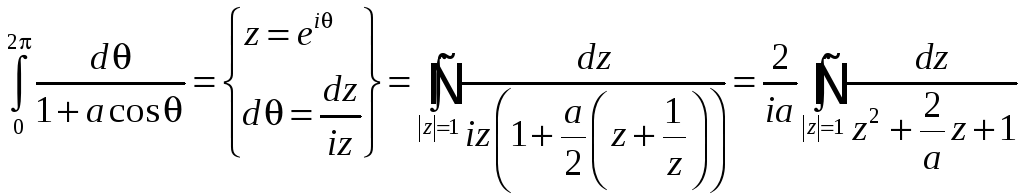 .
.
Особыми точками являются нули знаменателя
![]() (простые полюсы). Так как z1 z2 = 1,
то лишь один из них лежит внутри круга
|z| = 1. Легко видеть, что это –
точка
(простые полюсы). Так как z1 z2 = 1,
то лишь один из них лежит внутри круга
|z| = 1. Легко видеть, что это –
точка![]() .
Таким образом,
.
Таким образом,
 .
.
Окончательно![]() .
.
-
Вычисление интегралов типа
Лемма 15.1. Пусть f(z) – аналитическая функция в верхней полуплоскости Im z > 0 за исключением конечного числа изолированных особых точек, и существуют такие положительные числа R0, M и γ, что для всех точек |z| > R0 в верхней полуплоскости имеет место оценка
![]() . (15.1)
. (15.1)
Тогда
![]() , (15.2)
, (15.2)
где контур интегрирования C R – полуокружность |z| = R, в верхней полуплоскости Im z > 0.
Доказательство. Применяя свойство 5) (неравенство(6.6)) интеграла по комплексной переменной, получим
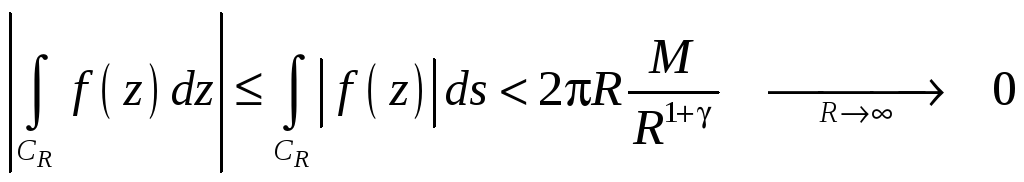 .
.
Доказательство закончено.
Теорема 15.18.
Пусть функция f(x), заданная на
действительной оси – ∞ < x < ∞,
может быть аналитически продолжена в
верхнюю полуплоскость Im z ≥ 0
и ее аналитическое продолжение f(z)
удовлетворяет всем условиям леммы 15.1
и не имеет на действительной оси особых
точек. Тогда несобственный интеграл
![]() существует и
существует и
![]() , (15.3)
, (15.3)
где zk (k = 1,2, … n) особые точки функции f(z) в верхней полуплоскости Im z > 0.
Доказательство. Пусть R > R0 (см. условия леммы 15.1). Рассмотрим замкнутый контур, состоящий из отрезка действительной оси R ≤ x ≤ R и полуокружности CR радиуса R с центром в начале координат в верхней полуплоскости Im z > 0. Радиус R выберем достаточно большим, чтобы все особые точки zk были расположены внутри этого контура. Тогда, согласно основной теореме о вычетах, имеем
![]() , (15.4)
, (15.4)
Так как выполнены условия леммы 15.1 то предел второго слагаемого в левой части (15.4) равен нулю, когда R ∞; правая часть (15.4) от R не зависит. Переходя в равенстве (14.4) к пределу при R ∞ получим утверждение (15.3). Доказательство закончено.
Пример 15.1.
Вычислить интеграл
![]()
Особые точки функции![]() ,
лежащие в верхней полуплоскости:
z1 = e¼ π i ,
z2 = e¾ π i.
Для вычисления вычетов воспользуемся
второй из формул (11.2). Имеем
,
лежащие в верхней полуплоскости:
z1 = e¼ π i ,
z2 = e¾ π i.
Для вычисления вычетов воспользуемся
второй из формул (11.2). Имеем
![]() .
.
-
Леммы Жордано
Леммы Жордано используются при нахождении преобразований Фурье и Лапласа и часто оказываются незаменимы в операционных исчислениях, построенных на базе этих преобразований.
Лемма 16.1 (лемма Жордано). Пусть функция f(z) является аналитической в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек, и равномерно относительно arg z (0 ≤ arg z ≤ π) стремится к нулю при |z| ∞. Тогда при a > 0
![]() , (16.1)
, (16.1)
где CR – дуга полуокружности |z| = R в верхней полуплоскости Im z > 0.
Доказательство. Условие стремления
f(z) к нулю при |z| ∞
равномерно относительно arg z в области
Im z > 0 означает, что существует
зависящая только от R = |z|
(то есть не зависящая от аргумента точки
z) функция![]() ,
оценивающая сверху функцию f(z)
для достаточно больших |z|=R:
,
оценивающая сверху функцию f(z)
для достаточно больших |z|=R:
![]() (16.2)
(16.2)
При интегрировании по окружности радиуса R удобно произвести замену z = R ei φ, dz = i R ei φ dφ, в результате получим
![]() .
.
Отсюда, учитывая (16.2) и тождество![]() ,
имеем
,
имеем

Используя очевидное неравенство
![]() ,
получаем оценку
,
получаем оценку
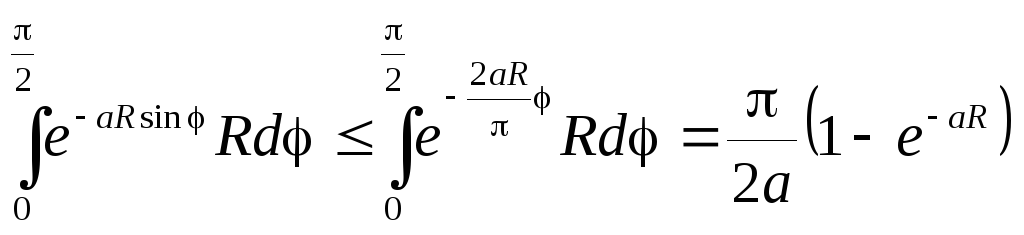 .
Окончательно
.
Окончательно .
Предельный переход в последнем соотношении
и завершает доказательство леммы.
.
Предельный переход в последнем соотношении
и завершает доказательство леммы.
Приведем еще несколько формулировок лемм Жордано, доказательства которых аналогичны предыдущему. Эти леммы применяются при вычислении соответствующих интегралов.
Лемма 16.2. Если в формуле (16.1) a < 0 и f(z) удовлетворяет условиям леммы 16.1 в полуплоскости Im z < 0, то формула (16.1) справедлива при интегрировании по дуге полуокружности |z| = R, Im z < 0.
Лемма 16.3. Если в формуле (16.1) a = i α (α > 0), и функция f(z) удовлетворяет условиям леммы 16.1 в полуплоскости Re z ≥ x0, (x0 любое действительное число), то
![]() ,
где
,
где![]() (16.3)
(16.3)
Лемма 16.4. Если в формуле (16.1) a = – i α (α > 0), и функция f(z) удовлетворяет условиям леммы 16.1 в полуплоскости Re z ≤ x0, (x0 любое действительное число), то
![]() ,
где
,
где![]() (16.4)
(16.4)
