-
Задачи для самостоятельного решения.
Вычислить интегралы по заданным контурам:
а)
;
б)
;
в)
2. Вычислить интегралы:
а)
;
б)
;
в)
.
-
отрезок, соединяющий точки
.
3. Используя формулу Ньютона-Лейбница, вычислить интегралы:
а)
,
б)
,
в)
,
г)
.
Вычислить интегралы, если все контуры обходятся против часовой стрелки:
4.
а)
,
б)
.
5.
а)
,
б)
.
6.
.
7.
.
-
Вычеты. Контурные интегралы
-
Классификация особых точек.
-
Точки области, в которых нарушается
аналитичность функции
,
называются особыми точками.
Точка
называется изолированной особой
точкой функции
,
если существует такая проколотая
окрестность этой точки (
),
если
конечна или
,
если
,
в которой нет особых точек. Различаются
три типа изолированных особых точек.
1. Устранимая особая точка. Точка
,
называется устранимой особой точкой,
если существует конечный предел функции
при
.
Функция, доопределенная в точке
равенством
,
станет аналитической в окрестности
точки
,
включая саму точку (в этом смысле она
называется " устранимой");
2. Полюс порядка
.
Точка
называется полюсом порядка m, если
и
(при
,
т.е. когда
,
полюс называется простым).
3. Существенно особая точка. Точка
называется существенно особой точкой,
если
не существует (ни конечный, ни бесконечный).
Методика определения особых точек типа полюс вытекает из теорем раздела 11 лекций.
Для того, чтобы
являлась полюсом порядка
для
необходимо и достаточно, чтобы функцию
можно было представить в виде
где
– функция аналитическая в точке
и
.
-
Примеры с решениями.
В примерах 5.1 – 5.5 найти изолированные особые точки и определить их тип.
Пример 5.1
.
Решение. Эта функция аналитическая
везде кроме точки
.
Имеем
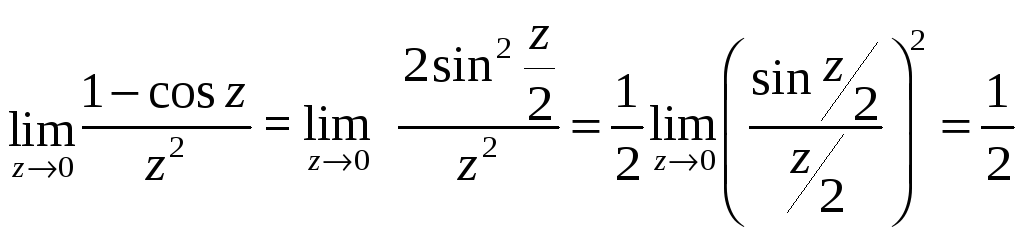
Следовательно, точка
является устранимой особой точкой.
Неаналитичность данной функции можно
устранить, положив
.
Пример 5.2
.
Решение. Функция не аналитическая
в точке
.
Рассмотрим числитель этой функции
и определим для него порядок нуля точки
.
Для этого найдем наименьший порядок
производной от
отличной от нуля в точке
:
Итак,
.
Следовательно, функция
представима в виде
,
где
аналитическая функция и
,
а функцию
можно записать так
Отсюда, в силу формулы (5.2), точка
есть полюс второго порядка.
Пример 5.3.
.
Решение. Аналитичность функции
нарушается в точке, где ее знаменатель
обращается в ноль, т.е. в точке
.
Определим порядок нуля в этой точке
числителя и знаменателя этой функции.
Введем обозначения
и
.
Имеем
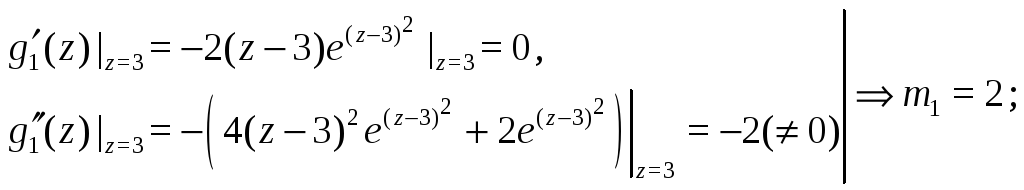
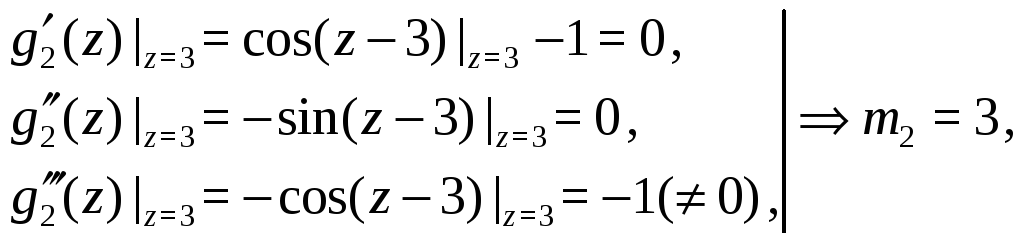
отсюда следует возможность представления
аналитических функций
и
в виде (5.1):
Таким образом, для функции
точка
есть простой полюс.
Пример 5.4
.
Решение. Функция
не является аналитической в точке
.
Рассмотрим поведение этой функции в
окрестности
.
Имеем
Но это означает, что предел функции при
не существует, т.е. точка
существенно особая.
В следующих примерах используйте методы решений примеров 5.1-5.4.
Пример 5.5
-
Вычеты. Вычисление контурных интегралов
Пусть
– изолированная особая точка функции
,
–
контур, охватывающий точку
,
причем
аналитическая в проколотой окрестности,
содержащей контур
, тогда вычетом функции
в точке
называется комплексное число, равное
.
Если
– полюс
-го
порядка, то
. 
Если
, где
– аналитические в точке
,
причем
является простым нулем
,
а
, то
. 
Основная теорема о вычетах. Пусть
функция
– аналитическая в области
за исключением конечного числа особых
точек
,
непрерывная в
, тогда
Таким образом, для вычисления контурных интегралов надо
1) найти особые точки функции
и убедится, что ни одна из них не лежит
на контуре интегрирования
;
2) выбрать те из них, которые лежат внутри контура;
3) вычислить вычеты в этих точках;
4) по формуле (5.6) найти искомый интеграл.