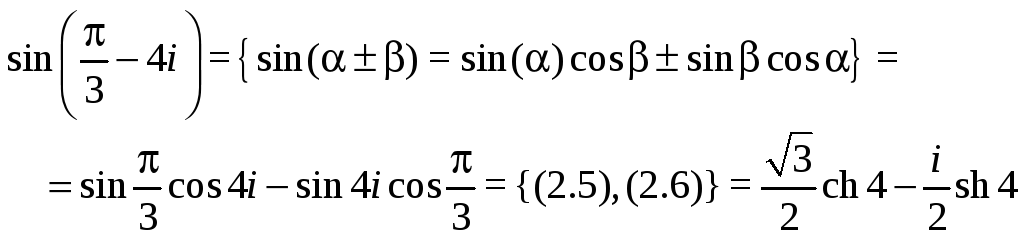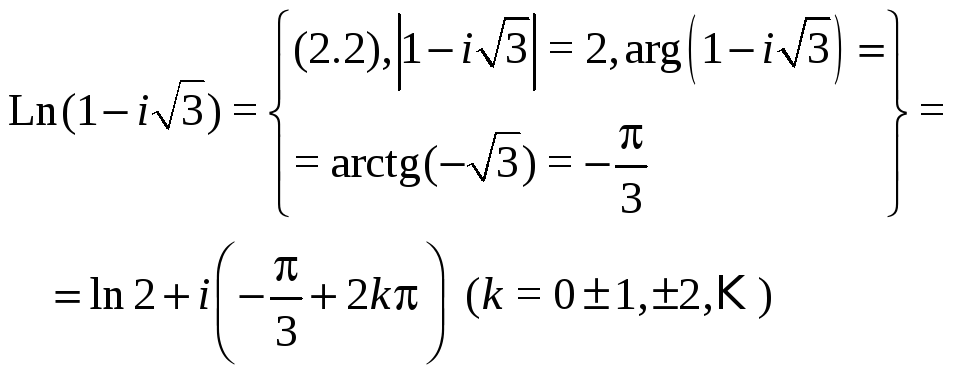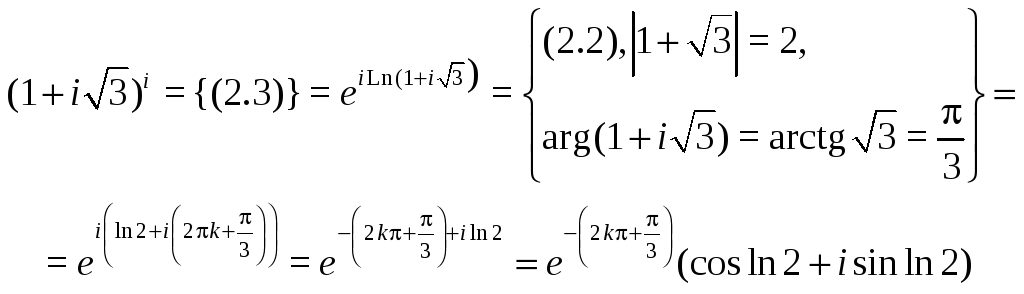- •Оглавление
- •Часть 1. Основы теории функций комплексной
- •Часть 2. Решение задач по теории функций
- •Предисловие
- •Часть 1. Основы теории функций комплексной переменной
- •Алгебра комплексных чисел
- •Различные формы представления комплексных чисел
- •Предел последовательности комплексных чисел
- •Расширение понятия комплексная плоскость
- •Сфера Римана
- •Функции комплексной переменной (фкп)
- •Степенные функции
- •Показательная функция
- •Тригонометрические функции
- •Гиперболические функции
- •Логарифмическая функция
- •Обратные тригонометрические функции
- •Предел, непрерывность, дифференцируемость
- •Аналитические функции
- •Свойства аналитических функций
- •Интеграл по комплексной переменной.
- •Основные свойства.
- •Теорема Коши
- •Неопределенный интеграл и формула Ньютона - Лейбница
- •Формула Коши
- •Представление аналитических функций степенными рядами
- •Ряды Тейлора.
- •Ряд Лорана.
- •Особые точки аналитической функции.
- •Классификация особых точек
- •Теоремы о вычетах
- •Об аналитическом продолжении
- •Вычисление интегралов типа
- •Вычисление интегралов типа
- •Леммы Жордано
- •Вычисление несобственных интегралов.
- •Интегралы типа
- •Контур Бромвича и интеграл Бромвича – Вагнера.
- •Функция Хевисайда и ее интегральные представления
- •Часть 2. Решение задач по теории функций комплексной переменной
- •Комплексные числа
- •Формы записи комплексных чисел
- •Примеры с решениями
- •Алгебраические операции над комплексными числами
- •Задачи для самостоятельного решения
- •Элементарные функции комплексного переменного
- •Представление элементарных функций комплексного переменного в алгебраической форме
- •Задачи для самостоятельного решения
- •Аналитические функции комплексного переменного
- •Дифференцируемость и аналитичность функций комплексного переменного.
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Интегрирование функций комплексного переменного
- •Вычисление интегралов. Теорема Коши. Интегральная формула Коши
- •Примеры с решениями
- •Задачи для самостоятельного решения.
- •Вычеты. Контурные интегралы
- •Классификация особых точек.
- •Примеры с решениями.
- •Вычеты. Вычисление контурных интегралов
- •Примеры с решениями
- •Задачи для самостоятельного решения
- •Вычисление определенных интегралов от действительных функций
- •Интегралы типа
- •Вычисление несобственных интегралов второго рода
- •Вычисление интегралов вида
- •Задачи для самостоятельного решения
- •Библиографический список
- •394000, Воронеж, пр. Революции, 19
-
Элементарные функции комплексного переменного
-
Представление элементарных функций комплексного переменного в алгебраической форме
-
Показательная функция комплексного
переменного
![]() определяется равенством
определяется равенством
![]()
![]()
Из определения видно, что это периодическая
функция с основным периодом![]() :
:![]() .
Основное свойство (также как у показательной
функции действительного переменного)
.
Основное свойство (также как у показательной
функции действительного переменного)![]() .
.
Логарифмическая функция. Эта функция
определяется как обратная показательной:
число w называется логарифмом числа
z, если![]() .
Обозначение:
.
Обозначение:![]() .
Следующее равенство можно принять за
определение логарифмической функции
комплексного переменного:
.
Следующее равенство можно принять за
определение логарифмической функции
комплексного переменного:
![]() .
. ![]()
В отличие от функции действительного переменного Ln z является многозначной функцией; значение при k = 0 называется главным значением или главной ветвью логарифмической функции в комплексной области и обозначается ln z:
![]()
Из определения вытекают основные функциональные свойства логарифмической функции:
![]() ,
,
![]()

Общие показательные и общие степенные функции.
Так называют функции комплексного переменного определяемые равенствами соответственно
![]()
![]()
Общая показательная и общая степенная функции комплексного переменного в являются многозначными. Тригонометрические функции определяются (посредством формулы Эйлера) через показательную:
![]()
![]()
Эти формулы также называются формулами Эйлера. По аналогии с функциями действительного переменного определяются функции tg z и ctg z:
![]()
![]()
Для тригонометрических функций комплексного переменного справедливы все формулы, справедливые для соответствующих функций действительного переменного. Для примера, исходя из формул (9.4) (9.5), докажите равенства
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Гиперболические функции определяются (как и тригонометрические) через показательную функцию.
Гиперболический синус
![]()
Гиперболический косинус
![]()
Гиперболический тангенс
![]()
Гиперболический котангенс
![]()
Из определений гиперболических и тригонометрических функций вытекают формулы
![]() ,
,
![]() ,
, ![]()
![]() ,
,
![]() .
. ![]()
Замечание. Любое соотношение,
справедливое между тригонометрическими
функциями переходит в соответствующее
соотношение между гиперболическими
функциями в результате формальной
замены функций
![]() и
и![]() .
Например, совершив указанную замену в
соотношениях
.
Например, совершив указанную замену в
соотношениях
![]() ,
,
![]()
получим следующие соотношения между гиперболическими функциями
![]() ,
,
![]() .
.
Обратные тригонометрические функции определяются как функции обратные тригонометрическим. Эти функции являются многозначными и выражаются через логарифмы комплексного переменного по формулам
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
Обратные гиперболические функции обозначаются соответственно Arsh z (ареасинус), Arch z (ареакосинус), Arth z (ареатангенс), Arcth z (ареакотангенс). Это опять многозначные функции, которые выражаются через логарифмы комплексного переменного по формулам
![]() ,
,
![]() (2.9)
(2.9)
![]() ,
,
![]() . (2.10)
. (2.10)
2.2 Примеры с решениями В задачах 1-7 значения соответствующих функций представить в алгебраической форме.
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|