1. Степенные функции

Пусть. Соотношением

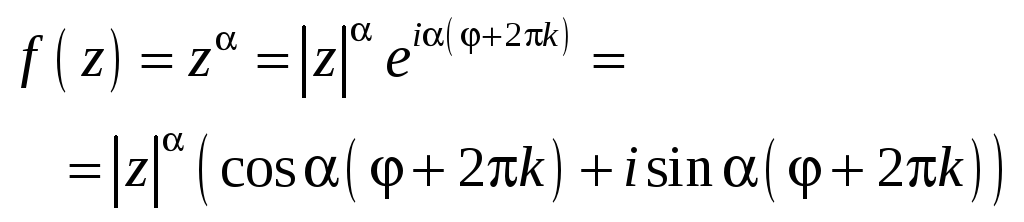
определены степенные ФКП. При    степенная функция является однозначной или простой. В остальных случаях говорят об общей степенной функции.

Общей степенной функцией также называют функцию w = z ^a комплексной переменной z, где a - фиксированное комплексное число. Функция определяется соотношением (определение логарифмической функции будет дано далее). Общая степенная функция комплексной переменной, в отличие от простейших степенных функций комплексного переменного, является функцией многозначной.

2. Показательная функция

Как известно, функции действительного переменного e^x, sin x, cos x раскладываются в степенные ряды, которые сходятся к этим функциям в любой точке действительной прямой. Из первой теоремы Абеля следует, что ряды, полученные заменой действительной переменной x на комплексную переменную z = x + iy, будут абсолютно сходится на  и тем самым определят функции комплексного переменного, которым присваиваются те же названия и обозначения:

, ,.

Кроме того, из равенств, определяющих эти функции и соотношения

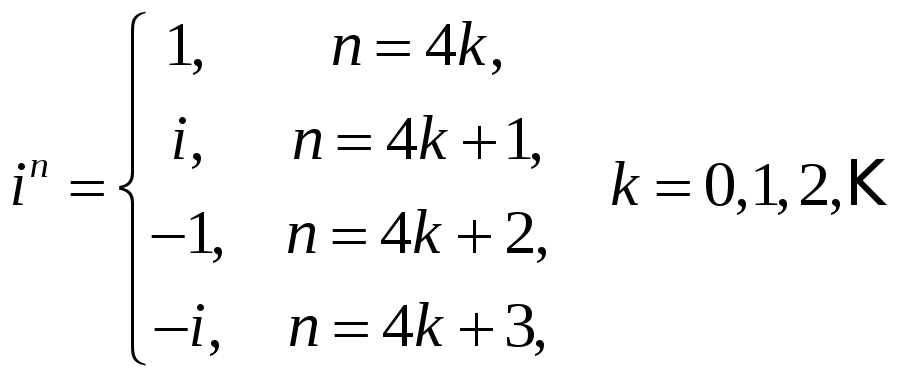
легко вытекает формула Эйлера

(3.1)

Из правила перемножения абсолютно сходящихся рядов (см.[2], стр. 642), следует и

.

Последнее равенство также можно принять за определение показательной функции комплексного переменного z. Важно подчеркнуть, что при таком определении легко проверяются известные для действительной переменной правила деления, умножения и возведения в степень. Также легко устанавливается новое свойство периодичности:. Геометрически это означает, что все точки z, расположенные на прямых, параллельных оси Оx и отстоящих друг от друга на расстояние, кратное 2 отображаются в одну точку комплексной плоскости w = u + i v.

3. Тригонометрические функции

Как и показательная, тригонометрические функции комплексного аргумента z определены соответствующими рядами, но гораздо удобнее воспользоваться формулой Эйлера (3.1) и определить их через показательную функцию:

, (3.2)

Эти формулы также называются формулами Эйлера. По аналогии с функциями действительного переменного

, (3.3)

Для тригонометрических функций комплексного переменного справедливы все формулы, справедливые для соответствующих функций действительного переменного. Для примера, исходя из формул (3.2) – (3.3), докажите равенства

sin²z + cos²z = 1, cos²z – sin²z = cos2z,

sin 2z = 2 sin z cos z,.

Замечание. Следует отметить, что найдутся такие значения комплексной переменной z, что |sin z| > 1 и |cos z| > 1. Таким образом, у функций комплексной переменной могут быть и существенные отличия от их действительнозначных аналогов.

4. Гиперболические функции

Используем показательную функцию для того, чтобы определить следующие функции комплексной переменной.

Гиперболические синус, косинус, тангенс и котангенс

, , ,.

Из этих определений вытекают формулы:

sh(i z) = i sin z , sin(i z) = i sh z , ch(i z) = cos z , cos(i z) = ch z.

5. Логарифмическая функция

Эта функция определяется как обратная показательной: число w называется логарифмом числа z, если e^w = z. Обозначение: w = Ln z. Представим это число в алгебраической форме. Полагая w = u + i v, одновременно имеем два равенства

z = e^w = e^u (cos v + i sin v), z = |z|(cos  + i sin ).

Откуда |z| = e^u  u = ln |z|; v =  + 2k, k = 0, 1,  2, … , где ln|z| – обычный логарифм действительного числа. Таким образом

Ln z = ln|z| + i (arg z + 2k). (3.4)

Это равенство примем за новое (равносильное первоначальному) определение логарифмической функции комплексного переменного. Как видим, в отличие от функции действительного переменного Ln z является многозначной функцией; значение при k = 0 называется главным значением или главной ветвью логарифмической функции в комплексной области и обозначается ln z:

ln z = ln|z| + i ,  = arg z, –  <   .

Основное функциональное свойство логарифмической функции

Ln(z₁z₂) = Ln z₁ + Ln z₂ (3.5)

в комплексной области доказывается так же как и в действительной:. По определению логарифма из последнего равенства следует (3.5).

Отметим также свойства, вытекающие из определения логарифмической функции.