
Kretov_vse
.pdf

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
г |
|
|
|
|
Рис. 7.2
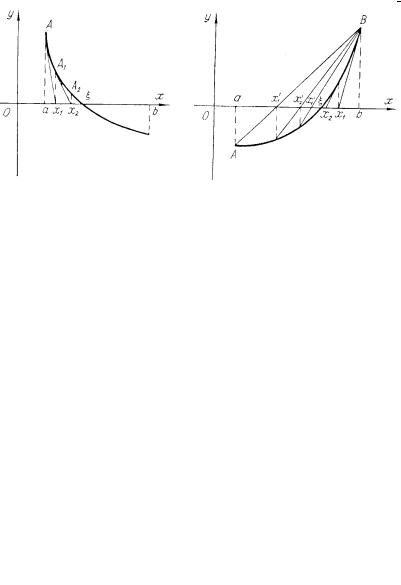
В первом случае за начальное приближение принимается а, то есть х0 = а, во втором — b, то есть x0 = b.
Последовательность чисел хn (n = 1, 2,…) сходится к корню ξ, то есть
lim xn = ξ.
n→∞
Вычисления приближений x1, x2 , x3 , … следует производить до тех пор, пока два соседних приближения xk , xk +1 не
совпадут на заданное число знаков.
Для промежуточных выкладок следует брать один-два запасных знака.
232
§ 7.6. ирЛ·ОЛКВММ˚В ПВЪУ‰˚ рВ¯ВМЛfl Ыр‡‚МВМЛИ
Если функция f(x) имеет отличную от нуля производную f '(x) на отрезке [a; b], то оценка абсолютной погрешности
определяется формулой
| ξ − xn |≤ |
| f (xn ) | |
, |
(7.6.8) |
|
µ |
|
|||
|
|
|
|
|
где
µ = min | f '(x) | .
a≤x≤b
Метод касательных (или метод Ньютона) состоит в сле-
дующем. Пусть на отрезке [a; b] находится единственный корень ξ уравнения (7.6.1). Проведем касательную к кривой y=f(x) в точке A[a; f(a)] до пересечения с осью Ох (рис. 7.3, а). Уравнение этой касательной имеет вид
y − f (a) = f '(a)(x − a) . |
(7.6.9) |
Полагая в этом уравнении у= 0, находим абсциссу х1 точки пересечения касательной с осью Ох:
x |
= a − |
f (a) |
(7.6.10) |
|
|||
1 |
f '(a) |
|
|
|
|
|
|
в предположении, что f '(a) ≠ 0 .
Абсциссу х1 точки пересечения касательной и оси Ох можно взять в качестве первого приближения корня.
а |
|
|
|
б |
|
|
|
|
|
|
|
Рис. 7.3
233
ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ
Проведя касательную через соответствующую точку А1[x1; f(x1)] и найдя точку ее пересечения с осью Ох, получим х2 — второе приближение корня. Аналогично определяются последующие приближения. В методе касательных n-е приближение вычисляется по формуле
xn = xn−1 − |
f (xn−1 ) |
(n = 1, 2, …), |
(7.6.11) |
|
f '(xn−1 ) |
||||
|
|
|
причем за начальное приближение х0 принимается такое значение х0 из отрезка [a; b], для которого выполняется условие
f (x0 ) f ''(x0 ) > 0 , |
(7.6.12) |
называемое условием Фурье.
Оценка погрешности определяется формулой (7.6.8). Комбинированный метод состоит в одновременном ис-
пользовании метода хорд и метода касательных. Его удобно применять, если на исходном отрезке [a; b] вторая производная f ''(x) сохраняет знак. В этом случае можно гарантировать
приближение к корню с двух сторон: касательная пересекает ось Ох со стороны выпуклости, а хорда — со стороны вогнутости графика функции у= f(x). Приближения по методу касательных будут располагаться с одной стороны корня, а приближения по методу хорд — с другой (рис. 7.3, б). Таким образом, получаются все более суживающиеся отрезки, внутри которых заключен корень. Длина последнего из отрезков дает величину абсолютной погрешности приближенного значения корня.
Если каким-либо способом получено приближенное значение х0 корня уравнения (7.6.1), то уточнение корня можно осуществить методом последовательных приближений, или
методом итераций. Для этого уравнение (7.6.1) представляют в виде
x = ϕ(x) , |
(7.6.13) |
234

§ 7.6. ирЛ·ОЛКВММ˚В ПВЪУ‰˚ рВ¯ВМЛfl Ыр‡‚МВМЛИ
что всегда можно сделать и притом многими способами, например
x = x + cf (x) , |
(7.6.14) |
где с — произвольная постоянная.
Пусть число х1 есть результат подстановки х0 в правую часть уравнения (7.6.13): x1 = ϕ(x0 ) , далее x2 =ϕ(x1 ) и
xn = ϕ(xn−1 ) . |
(7.6.15) |
Этот процесс последовательного вычисления чисел хn (n=1,2…) по формуле (7.6.15) называется методом последовательных приближений или методом итераций.
Процесс итераций сходится (lim x |
n |
= ξ) , если выполнено |
n→∞ |
|
|
условие |
|
|
| ϕ '(x) |≤ q <1 |
|
(7.6.16) |
на отрезке [a, b], содержащем корень ξ.
бДСДзаь
Графически отделить корни уравнений:
1929. |
ex + x = 0. |
1930. ex − 2x = 0. |
1931. 2e−x − x = 0. |
1932. |
e−x +3x = 0. |
1933. cosx − x = 0. |
1934. cosx +2x = 0. |
1935. |
ln x + x = 0. |
1936. 10ln x − x = 0. 1937. 2 lg x + x = 0. |
|
1938. |
5 lg x − x = 0. |
1939. ln | x | −x = 0. |
|
1940. |
3ln | x | +x = 0. |
1941. lg | x | +2x = 0. |
|
1942. |
lg | x | −3x = 0. |
1943. x ln x −1 = 0. |
|
1944. |
x lg x − 2 = 0. |
1945. x ln | x | +1 = 0. |
|
1946. |
x lg | x | +3 = 0. |
1947. x3 + x − 2 = 0. |
|
1948. |
x2 − 2x + 4 = 0. |
|
|
|
|
|
235 |

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ
Отделить корни уравнений: |
|
|
|||
1949. |
x3 |
+ x −3 = 0. |
1950. x3 |
+10x −9 = 0. |
|
1951. |
x3 |
−12x −8 = 0. |
1952. x3 |
+ 4x2 −6 = 0. |
|
1953. |
x4 +5x −3 = 0. |
1954. x5 |
+ 4x − 2 = 0. |
||
1955. |
x6 |
+ x −1 = 0. |
1956. x7 |
+ 6x −5 = 0. |
|
1957. |
ex |
− x − 2 = 0. |
1958. |
e−x + x −3 = 0. |
|
1959. |
ln x − 4 −2x = 0. |
1960. |
ln x − x +2 = 0. |
||
Методом хорд найти действительные корни уравнений:
1961. |
x3 |
+ x +1 = 0. |
1962. |
x3 |
− x −1 = 0. |
|
1963. |
x3 |
− x +1 |
= 0. |
1964. |
x3 |
+ x −1 = 0. |
1965. |
x4 |
+ 2x −1 = 0. |
1966. x4 +3x − 2 = 0. |
|||
1967. |
x4 |
+ 4x − 2 = 0. |
1968. x4 + 2x − 2 = 0. |
|||
1969. |
x5 |
+ x +1 = 0. |
1970. |
x5 |
− x +1 = 0. |
|
1971. |
x5 |
+ x −1 |
= 0. |
1972. |
x5 |
− x −1 = 0. |
Методом касательных найти действительные корни урав-
нений: |
|
|
|
|
|
1973. |
x3 + 2x −1 = 0. |
1974. |
x3 |
+3x − 2 = 0. |
|
1975. |
x3 −5x +1 = 0. |
1976. |
x3 |
− x2 +5 = 0. |
|
1977. |
x3 |
− x2 −3x + 2 = 0. |
1978. x3 + 2x2 − x −1 = 0. |
||
1979. |
x4 |
+ x −3 = 0. |
1980. x4 +3x +1 = 0. |
||
1981. |
x5 |
−3x +1 = 0. |
1982. |
x5 |
+ 2x +1 = 0. |
1983. |
e−x −3x + 4 = 0. |
1984. (x −1)2 −sin 2x = 0. |
|||
1985. |
2 lg x −(x −2)2 = 0. |
1986. shx −10thx + 2 = 0. |
|||
236 |
|
|
|
|
|

§ 7.6. ирЛ·ОЛКВММ˚В ПВЪУ‰˚ рВ¯ВМЛfl Ыр‡‚МВМЛИ
1987. chx +2x −3 = 0. |
1988. shx − x2 − 2 = 0. |
Комбинированным методом найти корни уравнений:
1989. |
x3 |
− 4x −5 = 0. |
1990. x3 − 2x +3 = 0. |
||
1991. |
x3 |
+ x2 + x − 2 = 0. |
1992. x3 − 2x2 − x +1 = 0. |
||
1993. |
x4 − 2x −1 = 0. |
1994. x4 − 4x + 2 = 0. |
|||
1995. |
ln x −(x −4)2 = 0. |
1996. ex −3(x +1)2 = 0. |
|||
1997. |
cosx − 2x + 0,5 = 0. |
1998. e−x − x2 − 2 = 0. |
|||
Методом итераций найти корни уравнений: |
|||||
1999. |
x3 |
− 2x + 7 = 0. |
2000. |
x3 |
−3x2 +1 = 0. |
2001. |
x4 +3x −1 = 0. |
2002. x4 +3x +1 = 0. |
|||
2003. |
x5 |
− 2x −3 = 0. |
2004. |
x5 |
+3x − 2 = 0. |
2005. |
x6 |
− x −1 = 0. |
2006. |
x6 |
+ x −1 = 0. |
2007. |
x7 |
+ x +1 = 0. |
2008. x7 −3x +1 = 0. |
||
§ 7.7. аТТОВ‰У‚‡МЛВ ЩЫМНˆЛИ Л ФУТЪрУВМЛВ „р‡ЩЛНУ‚
Достаточное условие возрастания (убывания) функции.
Если в данном промежутке производная данной функции положительная, то функция в этом промежутке возрастает. Если производная функции в некотором промежутке отрицательна, то функция в этом промежутке убывает.
Значение х1 из области определения функции f(х) называется точкой максимума этой функции, если существует такая δ-окрестность ]x1 – δ; x1 + δ[ точки х1, что для всех х≠х1 из этой окрестности выполняется неравенство f(x) < f(x1); значение функции f(x1) называется при этом максимумом функции f(x) и обозначается max f(x).
237
ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ
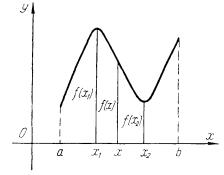
Значение х2 из области определения функции f(x) называется точкой минимума этой функции, если существует такая δ-окрестность ]x2 – δ; x2 + δ[ точки х2, что для всех х≠х2 из этой окрестности выполняется неравенство f(x) > f(x2); значение функции f(x2) называется при этом минимумом функции f(x) и обозначается min f(x).
Максимум и минимум функции называются экстремумом этой функции, а точки максимума и минимума — точками экстремума (рис. 7.4).
Рис. 7.4
Достаточное условие экстремума.
Первое правило. Если в точке х0 производная функции у= f(х) равна нулю и меняет знак при переходе через эту точку, то f(х0) — экстремум функции, причем: 1) функция имеет максимум при х= х0, когда знак производной меняется с плюса на
минус (то есть f '(x) > 0 , если x0 −ε < x < x0 , f '(x) < 0 , если x0 < x < x0 +ε , где ε > 0 ); 2) функция имеет минимум при х= х0, когда знак производной меняется с минуса на плюс (то есть f '(x) < 0 , если x0 −ε < x < x0 , f '(x) > 0 , если x0 < x < x0 +ε , где ε > 0 ).
238

§ 7.7. аТТОВ‰У‚‡МЛВ ЩЫМНˆЛИ Л ФУТЪрУВМЛВ „р‡ЩЛНУ‚
Второе правило. Если в точке х= х0 первая производная функции у= f(х) равная нулю, а вторая производная отлична от нуля, то х0 будет точкой экстремума, причем: 1) х0 — точка
максимума, если f ''(x0 ) < 0 ; 2) х0 — точка минимума, если
f ''(x0 ) > 0 .
Замечание 1. В случае f ''(x0 ) = 0 нужно обращаться к
первому правилу.
Замечание 2. Экстремум функции называют также ло-
кальным экстремумом, в отличие от глобального экстремума —
наибольшего (наименьшего) значения, которое функция может принимать в области ее определения. Чтобы найти глобальный экстремум функции f(x), заданный на отрезке [a; b], достаточно сравнить значения f(a), f(b) с ее значениями в точках локального экстремума на [a; b] и выбрать наибольшее (наименьшее) из них.
График функции у= f(х) называется вогнутым вверх (или выпуклым вниз) в промежутке ]а; b[, если соответствующая дуга кривой расположена выше касательной, проведенной в любой точке M(x; f(x)) этой дуги.
График функции называется у= f(х) вогнутым вниз (или выпуклым вверх) в промежутке ]а; b[, если соответствующая дуга кривой расположена ниже касательной, проведенной в любой точке M(x; f(x)) этой дуги.
Достаточное условие вогнутости (выпуклости) кривой.
Если вторая производная функции у= f(х) положительна в промежутке ]а; b[, то график этой функции вогнут вверх в
данном промежутке. Если вторая производная f ''(x) отрица-
тельна в промежутке ]а; b[, то график функции у= f(х) вогнут вниз в этом промежутке (сравните эти условия со вторым правилом нахождения экстремума).
Точкой перегиба непрерывной кривой называется ее точка, при переходе через которую каждая кривая меняет свою вогнутость на выпуклость, или наоборот (относительно, например, направления вниз).
239
ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ
Достаточное условие точки перегиба. Если для функции
у= f(х) вторая производная ее в точке х0 равна нулю и меняет знак при переходе через эту точку, то M(x0; f(x0)) — точка перегиба.
Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.
Если
lim f (x) = ∞ , |
(7.7.1) |
x→a |
|
топрямаях=аявляетсявертикальнойасимптотойкривойу=f(х).
Если существуют пределы
lim |
f (x) |
= k ; |
lim |
[ f (x) −kx]= b , |
(7.7.2) |
|
x |
||||||
x→±∞ |
|
x→±∞ |
|
|
то прямая y=kx+b есть наклонная асимптота кривой у=f(х).
Если в правой части уравнения кривой у= f(х) можно выделить линейную часть
y = f (x) = kx +b +α(x) , |
(7.7.3) |
где α(x) → 0 , когда x → ±∞ , то прямая y = kx +b |
является |
асимптотой.
Исследование функции можно проводить по следующей схеме:
1.Найти область определения функции.
2.Исследовать изменение функции при х, стремящемся к концам промежутков области определения.
3.Найти точки экстремума и промежутки возрастания и убывания функции.
4.Вычислить значения экстремумов.
5.Определить интервалы выпуклости и вогнутости графика, найти точки перегиба.
6.Найти точки пересечения графика функции с координатными осями.
7.Найти асимптоты графика функции.
240
