Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Kretov_vse

.pdf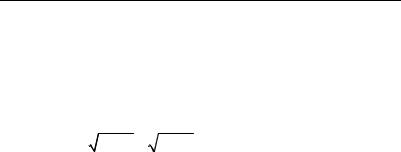

Скачиваний:

118

Добавлен:

23.03.2016

Размер:

3.26 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 5023 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

§ 7.4. ир‡‚ЛОУ гУФЛЪ‡Оﬂ

		x	−	1
1827. lim					.

x→1	x −1			ln x

1829. lim	ln(1− x) + x2	.
	(1+ x)5 −1+ x2
x→0

		1	−	1
1828. lim						.
				x	2
x→0	x sin x

	e−x −1+ x −				x2

1830. lim				2		.
	e	x	3
x→0				−1

4 3

1831. lim x4

(

+1 −

−1). 1832. lim

x − x

ln 1+

x→+∞

x→∞

−

1834. lim n

−

1833. lim 1+ x ln

3n +3

−2 .

x→∞

n→∞

− x −1

ex3

−1− x3

−

1835. lim

1836. lim

sin6

x→0

cosx +

−1

1837. lim

2x −1− x ln 2

−ctg

1838. lim

(1− x)

−1+ mx

x→0

1839. lim

−cos2 x

1840. lim

sin2

x −ln

2 (1+ x)

(1+ x2 )m −1

−1

x→0

sin x ctg

tgx

1841. lim

1842. lim

x→0

1843. lim

arccosx

1844. lim(2sin x)

ctg 6 x

x→0

x→π

ex −ea

x2cosx

1845. lim

1846. lim

x −a

cosx −1

x→a

x→0

221

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ

1847. lim

sin

ϕ −

2 tgϕ

1848. lim

ex −e−x

ϕ→π

1+cos4ϕ

x→0

ln(1+ x)

−esin x

1849. lim

1850. lim

e −(1+ x) x

x −sin x

x→0

1851. lim

x sin(sin x) −sin2 x

. 1852. lim

sin x − xcosx

sin3 x

x→0

1853. lim

ex −e−x

−2x

1854. lim

ln(1+ x2 )

x −sin x

cos3x −e−x

x→0

1855. lim

aln x −1

1856. lim

eax −e−ax

ln x

ln(1+ ax)

x→1

x→0

1857. lim

arc sin(2 − x)

1858. lim

2x − x4

− 3 x

x2 −3x + 2

1− 4 x3

x→2

x→1

1859. lim

x + 2 ln x

1860. lim

ex +sin x

x +sin x

x→∞

x→+∞

1861. limπ

tgx

−

1862. lim

−

−1

ln x

x→

1−sin x

x→1

1863. lim

ln(x2 −3)

−ctg

1864. lim

+3x

−

x→2

x→0

−

ln(1+ x)

ctgx

1865. lim

1866. lim

−

x→0

x(1+ x)

x→0

π x −1

−

1867. lim

1868. lim

x(e

2π x

π x

+1)

x→0

−1)

x→0

2x(e

222

§ 7.4. ир‡‚ЛОУ гУФЛЪ‡Оﬂ

1869. lim

−

. 1870. lim x2 x .

1871. lim xx

x→

ctgx

2cosx

x→+0

tgx

x tg

π x

sin−2 bx

2 −

1872. lim

1873. lim(cosax)

. 1874. lim

x→+0

x→0

x→a

tgx

1876. lim x

ln(ex −1)

−arctgx

1875. lim

. 1877. lim

x→0

x→+0

x→+∞ 2

1878. lim

(1+ x)

1879. lim n x lnm x.

x→∞

x→+0

1880. lim arc sin

x −a

ctg(x −a).

1881. lim (π − 2arctgx) ln x.

x→a

x→+∞

1882. lim (tgx)tg 2 x .

x→π4


			1
	tgx					1
				x2
1883. lim		x	.		1884. lim (cosax)x2 .
x→0					x→0

x x

π x

1885.

lim

arctgx .

1886. lim ln

1−

ctg

x→+∞

x→−a

1887.

lim (−ln x)x . 1888.

lim (tgx)sin 2 x . 1889. lim e −(1+ x) x .

x→+0

x→0

x→+ 2

1890.

lim

(a + x)x

−ax

x→0

−

1891. Найти lim

. Указание. Сделатьподстановку

x =

x→0

223

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ

−	1
−	x2
	x2	, x ≠ 0 в
1892. Найти производную функции f (x) = e		, x ≠ 0 в
		x = 0
0,		x = 0

точке х= 0. Указание. Воспользоваться определением производной и результатом задачи 1891.

1893. Построить функцию f(x), бесконечно дифференцируемую на всей прямой, не равную тождественно нулю и обращающуюся в нуль вне отрезка [– 4; 5].

1894. Показать, что lim	x −sin x	существует и равен 1, но

x→∞ x + cosx

не может быть вычислен с помощью правила Лопиталя. 1895. Применимо ли правило Лопиталя для вычисления

следующих пределов:

а) lim	x2	;	б) lim	e−ax	?
				−sin x −cosx)
x→+∞ x −sin x			x→+∞ e−x (2

Исследовать эти пределы, не пользуясь Правилом Лопиталя.

1896. Сравнить порядок роста при х→+ ∞ следующих функций с порядком роста степенных функций:

а) y = exβ −1, β > 0;	б) y = (ln x)β , β > 0 ;					в) y = shx ;
							1
г) y = xarctgx ;	д) y =	x +	x2	cos3	x	; е) y =	e− x			;
г) y = xarctgx ;	д) y =	x +	1	+ x2		; е) y =	1−e	−1		;
			1	+ x2				−1
									x
ж) y = xx −1;	з) y = ln(x ln x) .

1897. Сравнить порядок роста этих функций х→+ ∞ с порядком роста функций y= eax, y = exa , y = (lnx)a.

1898. Сравнить эти же функции при х→0 со степенями переменной х.

224

§ 7.5. оУрПЫО‡ нВИОУр‡

Пусть функция f имеет в некоторой окрестности точки а производные f ', f '',..., f (n) .Тогда для любой точки х из этой окрестности имеет место равенство:

f ( x) = f (a) +	f '(a)	( x − a) +	f ''(a)	(x − a)2 + ... +	f (n) (a)	+ R	( x) (7.5.1)

1!		2!			n !	n

при х→а.

Формула (7.5.1) называется формулой Тейлора. Остаточный член формулы ТейлораRn (x) обычно задается в двух

формах:

а) в форме Лагранжа

R	(x) =	f (n+1)(c)	(x − a)n+1 ,	(7.5.2)
		(n+1)!
n

где с — число из окрестности точки а, при этом предполагает-

ся существование f (n+1)			в данной окрестности точки а;
б) в форме Пеано:
		R	n	(x) = o((x − a)n ) .						(7.5.3)
			n
При а= 0 формула (7.5.1) называется формулой Маклорена
и имеет вид:
f (x) = f (0) +	f '(0)	(x) +			f ''()	x2 +... +		f (n) (0)	+ R	(x) . (7.5.4)
f (x) = f (0) +		(x) +				x2 +... +			+ R	(x) . (7.5.4)
1!					2!			n!	n
1!					2!			n!
Остаточный член этой формулы в форме Лагранжа будет
иметь вид:
	R (x) =				f (n+1)(θ)		xn+1,			(7.5.5)
	R (x) =						xn+1,			(7.5.5)
	n				(n+1)!

где 0 <θ <1, а в форме Пеано —

225

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ

(x) = o(xn ) .

(7.5.6)

Разложение по формуле Маклорена некоторых важнейших

элементарных функций:

ex =1+ x +

... +

+o(xn ) ,

(7.5.7)

sin x = x

−

− +... +

(−1)n x2n+1

+ o(x2n+2 ) , (7.5.8)

(2n +1)!

cosx =

1−

−... + (−1)

n x

+ o(x

2n+1

) , (7.5.9)

(2n)!

n−1 xn

ln(1+ x) = x −

−... + (−1)

+ o(x

) , (7.5.10)

α(α −1)

(1+ x)

=1+αx +

+...

(7.5.11)

α(α −1)...(α −n +1)

xn +o(xn ),

=1 + x + x2 +... + xn + o(xn ) ,

(7.5.12)

1− x

arc tg x = x −

−... +(−1)n

x2n+1

+o(x2 n+1

) . (7.5.13)

2n +1

бДСДзаь

1899. Разложить многочлен

f (x) = x4 + 2x3 −3x2 − 4x +1 по

степеням (х+ 1).

f (x) = x6

1900. Разложить многочлен

по степеням (x −1).

226

§ 7.5. оУрПЫО‡ нВИОУр‡

1901. Показать, что многочлен f (x) = x5 + 2x4 + x3 − x2 + +2x −1 имеет х= 1 корнем третьей кратности.

1902. Написать формулу Маклорена для функции ех и с помощью ее вычислить приближенное значение числа е с точностью до 0,0001.

1903. Показать, что при вычислении значений функции ех

0 < x ≤ 12 по формуле ех ≈1 + x + 12 x2 + 16 x3 погрешность мень-

ше 0,01. Найти	e с тремя верными цифрами.
1904. Показать,			что sin(a + h) отличается от sin a + hcosa
не более чем на	1	h	2	.
	2

1905. Написать формулу Маклорена для функции sin x и

определить значения х, для которых имеет место приближенная формула sin x ≈x с точностью до 0,001.

1906. Определить значения х,	при которых имеет место
приближенная формула sin x ≈x −	x3	с точностью до 0,001;
	6

0,0001. Вычислить с точностью до 0,0001 значения sin0,1, sin1°, sin 10°, sin 20° и сравнить с табличными данными.

1907. Написать формулу Маклорена для функции соs x и определить значения х, для которых имеет место приближен-

ная формула cos x ≈1− x2 , с точностью до 0,0001. Вычислить

с точностью до 0,0001 соs 0,1, соs 1°, соs 5°, соs 10°, и сравнить с табличными данными.

1908. Показать, что 1 + x =1+	1	x −	1	x2 +		x3	, где
						5
2		8
					16(1	+θ x)2

0 < Ө< 1 и оценить погрешность приближенного равенства

1+ x ≈1 + 12 x − 18 x2 для 0 < x < 12 .

227

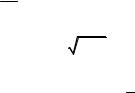
ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ

1909. Выяснить происхождение приближенного равенства


sin x ≈ x +			x3	и оценить его погрешность для 0 < x <			1	.
sin x ≈ x +		6		и оценить его погрешность для 0 < x <		2		.
		6				2
1910. Выяснить происхождение приближенного равенства
tg x ≈ x +	x3			и оценить его погрешность для 0 ≤ x ≤	1	.
tg x ≈ x +		3		и оценить его погрешность для 0 ≤ x ≤	3	.
		3			3

Написать формулу Маклорена с тремя членами для следующих функций:

1911. y =	1	.	1912. y =	ex + e−x	.
	+ x			2
1

1913. y = esin x . 1914. y = ln(1+ sin x).

Доказать неравенства (1915—1918):

1915.	tg x > x +	x3	при 0 < x <			π	.
1915.	tg x > x +	3	при 0 < x <			2	.
		3				2
1916. arc sin x > x +				x3	при 0 < x <1 .
1916. arc sin x > x +			6		при 0 < x <1 .
			6

1917. x − x2 < ln(1 + x) < x при x >0.

1918.	1+	1	x −	x2	< 1+ x <1 +	1	x	при 0 < x < 8 .
		2		8		2

1919.Записать функцию y = 1x по формуле Тейлора в ок-

рестности точки х= 3.

1920. Записать функцию y = cos(x +α) по формуле Маклорена.

228

§ 7.5. оУрПЫО‡ нВИОУр‡

Разложить заданные функции по формуле Маклорена:

I921. y =

1− x2

1922. y = cos2 x.

Указание.

Воспользуйтесь формулой:

cos2 x =

1+ cos2x

1923. y =

1+ x

(1− x2 )2

Вычислить данные интегралы путем разложения подынте-

гральной функции по формуле Маклорена:

3 1− x3 −1

1924. ∫e

dx.

1925. ∫

dx.

1926. Функцию

y = ln(x +

1+ x2 ) разложить по формуле

Маклорена, исходя из соотношения

ln(x +

1+ x2 ) = ∫x

1+ x

Пользуясь разложением функции по степеням х, вычис-

лить пределы выражений:

1927. lim

ln(1+ x + x2 ) +ln(1− x + x2 )

x(ex −1)

x→0

−

ctgx

1928. lim

x→0

229

ЙО‡‚‡ VII. СЛЩЩВрВМˆЛ‡О¸МУВ ЛТ˜ЛТОВМЛВ ЩЫМНˆЛЛ У‰МУИ МВБ‡‚ЛТЛПУИ ФВрВПВММУИ

§ 7.6. ирЛ·ОЛКВММ˚В ПВЪУ‰˚ рВ¯ВМЛﬂ Ыр‡‚МВМЛИ

Определение 1. Корнем уравнения
f(x) = 0	(7.6.1)

называется такое значение х = хо аргумента функции f(x), при котором это уравнение обращается в тождество, то есть

f (x0 ) ≡ 0 . Корень уравнения (7.6.1) геометрически представ-

ляет абсциссу общей точки графика функции у= f(x) и оси Ох. Отделить корень уравнения (7.6.1) это значит найти такой промежуток, внутри которого имеется корень данного уравнения, причем этот корень является единственным в данном

промежутке.

Отделение корней уравнения (7.6.1) можно выполнить графически, если удается построить график функции у= f(x), по которому можно судить о том, в каких промежутках находятся точки пересечения его с осью Ох.

Часто бывает затруднительным построить график функции у= f(x); тогда следует представить уравнение (7.6.1) в эквивалентном виде

f1(x) = f2(x)

(7.6.2)

с таким расчетом, чтобы графики функций у= f1(x) и у= f2(x) строились по возможности проще. Корень уравнения (7.6.2) геометрически представляет абсциссу точки пересечения гра-

фиков функций у= f1(x) и у= f2(x).

Для отделения корней уравнения (7.6.1) применяют следующий критерий: если на отрезке [a; b] функция f(x) непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке имеется один и только один корень уравнения. Достаточным признаком монотонности функции f(x) на данном отрезке является сохранение знака первой ее производной (если f '(x) > 0 , функция воз-

растает на данном отрезке, если f '(x) < 0 , функция убывает).

230

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 5023 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.2015178.79 Кб154Kopia_testy_dlya_farmy_studentam_s_otvetami.docx
#
20.11.2018110.59 Кб6Kosti_tulovishcha-449.doc
#
16.11.2019112.64 Кб10KP.doc
#
24.09.2019614.91 Кб6Kratky_konspekt_lektsy_pravo.doc
#
23.03.20161.05 Mб123Kretov1.pdf
#
23.03.20163.26 Mб118Kretov_vse.pdf
#
23.03.2016543.23 Кб145kuharenko_v_a_praktikum_po_stilistike_angliiskogo_yazyka.doc
#
25.08.2019126.74 Кб11Kultura_kontrolnaya_dopolnennoe.docx
#
22.09.2019416.92 Кб5Kumleva_T_Samaya_Sovremennaya_Fraze.docx
#
20.11.2019162.82 Кб4kursOS.doc
#
27.10.2018335.87 Кб15Kuznecov.doc