
Kretov_vse
.pdf
§5.4. ирflП‡fl Л ФОУТНУТЪ¸ ‚ ФрУТЪр‡МТЪ‚В
842.Найти координаты точки пересечения прямой
x 2−1 = y 1+ 2 = z −1 2 с плоскостью 3x –y +2z+5 = 0.
843. Найти координаты проекции точки М(2; 2; – 2) на плоскость 3x –y +z–13 = 0.
844. |
При каком значении m прямая |
x +10 |
= |
y − 7 |
= |
z + 2 |
||||||
|
|
|
|
|
||||||||
|
|
m |
|
|
2 |
|
|
|
− 6 |
|||
параллельна плоскости 5x – 3y +4z–1= 0? |
x −3 |
|
y −3 |
|
z |
|||||||
845. |
При каких значениях С и D прямая |
= |
= |
|||||||||
|
−3 |
|
||||||||||
|
|
|
2 |
|
|
7 |
||||||
лежит в плоскости 2x –y +Cz+D = 0?
846. Составить уравнение плоскости, проходящей через пря-
x + 2y − z + 2 |
= 0, |
|
x =1−t, |
|
|
|
|||
мую |
3x − y + z −5 |
= 0 |
параллельно прямой y = −2 + 2t, |
|
|
|
z =1+ 2t. |
||
|
|
|
|
|
847.Найти уравнение плоскости, проходящей через ось Ох
иобразующей с плоскостью  2 x+y–z+2=0 угол, равный 45º.
2 x+y–z+2=0 угол, равный 45º.
848.Найти уравнение плоскости, проходящей через пря-
2x − y + z −3 |
= 0, |
и отсекающей на оси Оу отрезок, |
мую |
= 0 |
|
x + y −3z −1 |
|
равный 3.
849. При каких значениях р и В прямая x 3−1 = y−+42 = z −p 3
перпендикулярнаплоскости6x+Вy–3z+1=0?
850. При каком значении А плоскость Аx – 2y +4z+5 =0 па-
y − z = 0,
раллельна прямой ?
x + y = 0
851. Каково уравнение прямой, проходящей через точку О(0; 0; 0) перпендикулярно к плоскости x +y +z+1 =0?
141

ЙО‡‚‡ V. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl ‚ ФрУТЪр‡МТЪ‚В
852. Найти уравнение проекции прямой |
x |
= |
y +1 |
= |
z +1 |
|
||
5 |
− 2 |
|
−3 |
|
||||
|
|
|
||||||
на плоскость, заданную уравнением 2x – 3y +z– 4 =0.
§ 5.5. иУ‚ВрıМУТЪЛ ‚ЪУрУ„У ФУрfl‰Н‡
Если в евклидовом пространстве R3 ввести прямоугольную систему координат Oxyz, то каждая поверхность определяется некоторым уравнением
F(x; y; z) =0, |
(5.5.1) |
где (x; y; z) — координаты любой точки поверхности.
Если F(x; y; z) — многочлен не выше второй степени относительно совокупности переменных x; y; z, то уравнение F(x; y; z)=0 называется уравнением второго порядка, а поверхность, изображаемая этим уравнением, называется поверхностью второго порядка.
иУ‚ВрıМУТЪЛ ‚ЪУрУ„У ФУрfl‰Н‡ Л Лı Н‡МУМЛ˜ВТНЛВ Ыр‡‚МВМЛfl
|
Эллипсоид |
|
Однополостный |
|
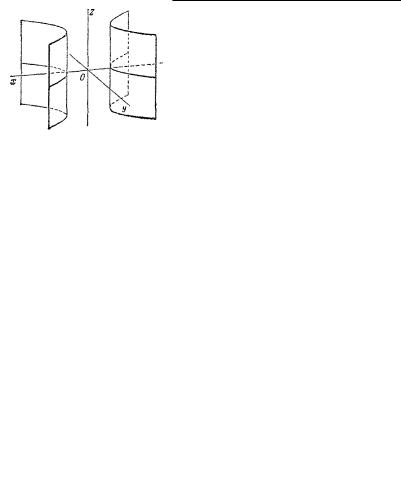
Двуполостный |
|||||||||||||
|
|
|
гиперболоид |
|
гиперболоид |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
x2 |
+ |
y2 |
+ |
z2 |
=1 |
x2 |
+ |
y2 |
− |
z 2 |
=1 |
x2 |
+ |
y2 |
− |
z 2 |
= −1 |
|
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
a2 |
b2 |
c2 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
142
§ 5.5. иУ‚ВрıМУТЪЛ ‚ЪУрУ„У ФУрfl‰Н‡
Эллиптический
параболоид
z = x2 + y2 a2 b2
Эллиптический
x2 |
+ |
y2 |
=1 |
|
a2 |
b2 |
|||
|
|
Гиперболический Конус параболоид (седло)
z = |
x2 |
− |
y2 |
|
x2 |
+ |
y2 |
− |
z 2 |
= 0 |
a2 |
b2 |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
|
|
Цилиндры Гиперболический Параболический
x2 |
|
y2 |
|
|
|
− |
|
=1 |
y2 =2px |
a2 |
b2 |
|||
Сфера — частный случай эллипсоида. Ее каноническое уравнение имеет вид: x2 +y2 +z2 =R2. Сфера радиуса R с центром в точке М0(x0; y0; z0) имеет уравнение:
(x – x0)2 +(y –y0)2 +(z – z0)2 =R2. |
(5.5.2) |
143

ЙО‡‚‡ V. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl ‚ ФрУТЪр‡МТЪ‚В
Если задано уравнение той или иной поверхности, то возникает задача исследования ее формы и расположения относительно координатных осей, Для решения этой задачи обычно применяют метод параллельных сечений: поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и размер полученных сечений позволяют выяснить геометрическую форму самой поверхности.
Линию в пространстве R3 можно определить как пересечение двух поверхностей:
F(x; y;z)=0,
1 (5.5.3)
F(x; y;z)=0.
2
Для исследования линии удобно воспользоваться цилиндром, проектирующим ее на ту или иную координатную плоскость. Если, например, проектируем линию на плоскость Oxy, то исключим z из системы (5.5.3) и получимуравнение φ(x; y)=0. Оно изображает направляющую проектирующего цилиндра на плоскость Oxy. В зависимости от того, будет ли φ(x; y)=0 эллипсом, гиперболой, параболой, парой прямых, — изучаемая линия сохранит соответствующее название.
бДСДзаь
853.СоставитьуравнениесферысцентромвточкеМ0(–5; 3; 2)
икасающейся плоскости 2x –2y +z–4=0.
854.Составить уравнение сферы с центром в точке М0(0; 4; 0), если она касается плоскости 2x +6y –3z– 3 =0.
855.Составить уравнение сферы, касающейся двух парал-
лельных плоскостей 6x – 3y –2z– 35 =0 и 6x –3y –2z+63 =0, ес-
ли центр расположен на прямой |
x −11 |
= |
y + 4 |
= |
z +3 |
. |
|
6 |
|
−3 |
|
||||
|
|
|
|
−2 |
|||
856.Составить уравнение сферы радиуса R =9, проходя-
щей через точки A(– 5; 10; – 1), B(1; –2; 1), C(–8; –2; 2).
857.Сфера проходит через три точки A(–2; 4; 1), B(–5; 0; 0), C(3; 1; –3), а ее центр лежит на плоскости 2x +y – z+3 =0. Составить ее уравнение.
144

§ 5.5. иУ‚ВрıМУТЪЛ ‚ЪУрУ„У ФУрfl‰Н‡
858.Составить уравнение сферы, проходящей через четы-
ре точки: A(1; – 2; – 1), B(4; 1; 11), C(– 8; –2; 2), D(– 5; 10; –1).
859.Составить уравнение сферы, проходящей через четы-
ре точки: O(0; 0; 0), A(2; 0; 0), B(1; 1; 0), C(1; 0; –1).
860.Составить уравнение сферы, если:
а) точки A(3; – 2; 6) и B(5; 2; – 2) являются концами одного из ее диаметров;
б) имеет центр в точке М0(5; 0; 3) и проходит через точку А(4; 1; –1);
в) имеет центр в точке М0(2; 1; 3) и касается плоскости z=6; г) имеет центр в точке М0(5; 2; –1) и касается плоскости
2x –y +3z+23 =0;
д) она симметрична сфере (x −1)2 +( y −3)2 +(z + 4)2 = 46
относительно плоскости 3x + y – 2z = 0;
е) она проходит через точки A(1; – 6; – 2), B(4; – 3; 2),
C(– 3; – 3; 9) и D(4; 1; 6). |
|
|
|
|
|
|
|
|
861. Найти точки пересечения поверхности |
|
x2 |
+ |
y2 |
− |
z2 |
=1 |
|
16 |
9 |
4 |
||||||
|
|
|
|
|||||
ипрямой x4 = −y3 = z +4 2 .
862.При каких значениях параметра p плоскость 2x–2y–z=p касается сферы x2 +y2 +z2 =81?
863.Установить, при каких m плоскость y +mz =1 пересекает двуполостный гиперболоид x2 +y2 – z2 =– 1:
а) по эллипсу; б) по гиперболе.
864.Установить, при каких m плоскость my +z=2 пересе-
кает эллиптический параболоид y = |
x2 |
+ |
z 2 |
: |
|
3 |
2 |
||||
|
|
|
а) по эллипсу; б) по параболе.
865. Установить тип заданных поверхностей и построитьих:
а) |
x2 |
+ |
y2 |
+ |
z 2 |
=1; |
б) x2 +y2 – 4z2 =– 1; |
|
4 |
16 |
81 |
||||||
|
|
|
|
|
145

ЙО‡‚‡ V. ДМ‡ОЛЪЛ˜ВТН‡fl „ВУПВЪрЛfl ‚ ФрУТЪр‡МТЪ‚В
|
в) 3x2 +y2 =2a(z– 2); |
|
|
|
|
|
|
|
|
г) 2y =x2 – |
z |
2 |
; |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
д) y2 =15z; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е) z=5 – x2 –y2; |
|
|
|
|
|
|
||||||||||||
|
ж) x2 – 9y2 =4z2; |
|
|
|
|
|
|
|
|
|
|
з) x2 =5y – 1; |
|
|
|
|
|
|
|
|
||||||||||||||
|
и) 2x2 – 4x +y2 – 6y – z2 =0; |
к) 2x2 – 7y2 +11z2 =0; |
|
|
|
|||||||||||||||||||||||||||||
|
л) x +2 =y2 –3y +3y +3z2 +6z; |
м) x2 =yz. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
866. Определить линию пересечения поверхностей |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
(x – 4)2 +(y – 7)2 +(z+1)2 =36 |
и 3x +y– z– 9 =0. |
|
|
|
|||||||||||||||||||||||||||
|
|
867. Исследовать |
|
|
линию |
пересечения |
|
|
|
гиперболоида |
||||||||||||||||||||||||
|
x2 |
+ |
y2 |
|
− z 2 |
=1c плоскостью 4x– 3y – 12z– 6 =0, пользуясь ее |
||||||||||||||||||||||||||||
9 |
|
|||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
проекциями на координатные плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
868. Установить, |
какие линии определяются |
|
системами |
|||||||||||||||||||||||||||||
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
(x −1) |
2 |
|
|
( y + |
1) |
2 |
|
|
|
|
(x − |
1) |
2 |
|
|
( y + |
1) |
2 |
|
||||||||||
|
2z = |
|
|
|
+ |
|
|
|
|
2z = |
|
|
− |
|
|
|
||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
, |
|
|
|
4 |
|
|
3 |
|
, |
||||||||||||
а) |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
б) |
|
|
|
|
|
|
||||||||||||
|
|
3x − y +6z −18 |
= 0. |
|
|
|
|
|
x − 2y −1 |
= 0. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(x −1) |
+ |
( y |
+1) |
− |
z |
=1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
9 |
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
9x − 6y + 2z − 43 = |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
869. Методом параллельных сечений исследовать геометрическую форму поверхностей, заданных уравнениями:
а) |
x2 |
+ |
|
y2 |
|
− |
z 2 |
=1; |
б) |
x2 |
|
+ |
|
y2 |
+ |
|
|
z 2 |
=1; |
|
|
|
|
|
|||||||||
9 |
|
16 |
|
25 |
9 |
|
|
|
4 |
|
16 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в) |
x2 |
|
+ |
|
y2 |
|
− |
z 2 |
|
=1; |
г) z = |
|
|
|
x2 |
|
+ |
|
y |
2 |
|
; |
д) z = |
x2 |
− |
y2 |
; |
||||||
9 |
|
|
25 |
|
4 |
|
|
|
4 |
|
|
9 |
|
|
4 |
|
9 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
е) |
x2 |
+ |
|
y2 |
=1; |
|
|
ж) |
|
x |
2 |
|
− |
|
y |
2 |
|
=1; |
з) x2 = 2y. |
|
|
|
|||||||||||
4 |
|
9 |
|
|
4 |
|
|
9 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
146 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

§ 5.5. иУ‚ВрıМУТЪЛ ‚ЪУрУ„У ФУрfl‰Н‡
870. Дан гиперболический параболоид x2 – |
y2 |
= z и одна |
|
4 |
|||
|
|
из его касательных плоскостей: 10x –2y – z–21 =0. Найти уравнения каждой из тех двух прямых, по которой плоскость касается с параболоидом.
871. Доказать, что плоскость 4x – 5y –10z–20 =0 пересекает
однополостный гиперболоид |
x2 |
+ |
y2 |
− |
z 2 |
=1 по прямоли- |
|
25 |
16 |
4 |
|||||
|
|
|
|
нейным образующим. Составить уравнения этих образующих.
147

É Î ‡ ‚ ‡ V I
ЗЗЦСЦзаЦ З еДнЦеДнауЦлдав ДзДгаб
§ 6.1. îÛÌ͈ËË Ë Ëı „ð‡ÙËÍË
Пусть имеется два множества X и Y.
Определение 1. Функцией f множества X в множество Y называется закон, по которому каждому элементу x X ставится в соответствие один или много элементов y Y.
Если каждому элементу x X ставится в соответствие лишь один элемент y Y, то функция f называется однозначной, при этом пишут y = f(x). Переменная х при этом называется независимой переменной (или аргументом), а переменная у — зависимой.
Множество Х называется областью определения данной функции и обозначается D(f), а множество всех чисел у, соответствующих различным числам x X, — областью значений этой функции и обозначается Е(f).
Пусть задана прямоугольная система координат Оху и функция y = f(x).
Определение 2. Графиком функции f(x) называется множество всех точек плоскости с координатами (х; f(x)), где х D(f).
График функции y = f(x) можно построить с помощью сдвигов и растяжений:
1)график функции y = f(x) + а получается из графика функции y = f(x) сдвигом вдоль оси Оу на |a| единиц (вверх, если
а> 0, и вниз, если a < 0);
2)график функции y = f(x – b) получается из графика функции y = f(x) сдвигом вдоль оси Ох на |b| единиц (вправо, если b > 0, и влево, если b < 0);
3)график функции y = kf(x) получается из графика функции y = f(x) растяжением вдоль оси Оу в k раз;
148

§ 6.1. îÛÌ͈ËË Ë Ëı „ð‡ÙËÍË
4)график функции y = f(mx) получается из графика функции y = f(x) сжатием по оси Ох в m раз;
5)график функции y = – f(x) получается из графика функции y = f(x) симметричным отражением относительно оси Ох;
6)график функции y = f(– x) получается из графика функции y = f(x) симметричным отражением относительно оси Оу.
Определение 3. Функция f называется четной, если множе-
ство D(f) симметрично относительно нуля и для любого
х D(f) имеет место f(– x) = f(x).
График четной функции симметричен относительно оси Оу. Определение 4. Функция f называется нечетной, если множество D(f) симметрично относительно нуля и для любого
х D(f) имеет место f(– x) = – f(x).
График нечетной функции симметричен относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
Определение 5. Функция f называется периодической, если существует такое число Т ≠ 0, что для любого х D(f) выполня-
ютсяусловия: а) х–Т D(f), х+Т D(f); б) f(x–Т)=f(x+Т)=f(x).
Под периодом функции обычно понимают наименьший из ее положительных периодов.
Определение 6. Пусть область значений функции y = f(x) содержится в области определения функции d(y). Тогда функция z = d(f(x)), х D(f) называется сложной функцией.
Определение 7. Функция f называется неубывающей (невозрастающей) на множестве Х D(f), если для любых значений х1, х2 Х таких, что х1 < х2, справедливо неравенство f(x1) ≤ f(x2) (соответственно, f(x1) ≥ f(x2)).
Функция f называется монотонной, если она невозрастающая или неубывающая.
Определение 8. Функция f называется возрастающей (убывающей) на множестве Х D(f), если для любых значений х1, х2 Х таких, что х1 < х2, справедливо неравенство f(x1) < f(x2) (соответственно, f(x1) > f(x2)).
Функция называется строго монотонной, если она возрастающая или убывающая.
149

ЙО‡‚‡ VI. З‚В‰ВМЛВ ‚ П‡ЪВП‡ЪЛ˜ВТНЛИ ‡М‡ОЛБ
Определение 9. Пусть для любых различных значений х1, х2 D(f) имеет место f(x1) ≠ f(x2). Тогда для любого у E(f) найдется только одно значение x = d(y) D(f), такое, что y = f(x). Функция d, определенная на E(f), называется обратной для функции f и обозначается: х= f – 1(у).
Пусть функция y = f(x) |
возрастает (убывает) на отрезке |
[a; b]. Тогда на отрезке |
[ f (a); f (b)] (соответственно, |
[ f (b); f (a)]) определена возрастающая (убывающая) функ-
ция d, обратная для функции f.
График функции d, обратной для функции f, симметричен графику f относительно прямой у= х.
Определение 10. Функция y = f(x) называется ограниченной на множестве Х D(f), если существует такое число М> 0, что
|f(x)| ≤ M для всех x X.
Определение 11. Функция, заданная формулой |
|
y = f(x), |
(6.1.1) |
называется явной функцией.
Определение 12. Функция у= у(х), заданная с помощью
уравнения |
|
F(x, y) = 0, |
(6.1.2) |
называется неявной функцией.
Определение 13. Пусть на некотором множестве Х R заданы две функции х= х(t) и у= у(t). Тогда множество всех точек на плоскости Оху с координатами (х(t); у(t)), где t X, называется кривой, заданной параметрически.
Определение 14. Если кривая, заданная параметрически, является графиком некоторой функции у= f(х), то эта функция также называется функцией, заданной параметрически.
Гиперболическими функциями называются следующие четыре функции:
1) гиперболический синус у= sh x,
sh x = |
ex − e−x |
; |
(6.1.3) |
|
2 |
||||
|
|
|
150
