7. Метрические задачи

Метрическими называются задачи, в которых приходится определять значения измеряемых величин - измерять величину угла между' двумя прямыми и расстояние между двумя точками.

К метрическим относятся также задачи на построение угла и отрезка с наперед заданным соответственно градусной и линейной величины.

В основе алгоритма решения любой метрической задачи лежит свойство плоской фигуры, параллельной плоскости проекций: она (фигура) проецируется на эту плоскость в конгруентную фигуру;

фаФаФ.

В задачах на построение проекций угла, равного 90°, используется теорема о частном случае проецирования прямого угла: прямой угол проецируется ортогонально без искажения, если одна из его сторон параллельна плоскости проекции, а вторая сторона не перпендикулярна к этой плоскости:

([АВ][ВС])([АВ],ВС)А^В^В^С^

Рис 7.1

При определении расстояния между двумя точками или построении отрезка заданной длины можно использовать как методы преобразования ортогональных проекций, так и пользоваться построением прямоугольного треугольника.

Отметим ряд свойств ортогональных проекций плоских углов(доказательства рассмотреть самостоятельно).

п

88

рямой. 1 Если стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость с искажением.

2. Если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол:

а) проекция острого угла будет меньше проецируемого угла;

б) прямой угол проецируется без искажения;

в) проекция тупого угла больше проецируемого угла,

3.Если обе стороны любого угла параллельны плоскости проекции, то на эту плоскость он проецируется без искажения.

4.Проекции острого и тупого углов могут проецироваться на плоскость без искажения не только при условии параллельности сторон угла плоскости проекции.

5. Если стороны угла параллельны плоскости проекции или одинаково наклонены к ней, то деление пополам проекции угла соответствует его делению пополам в пространстве.

Если проекция некоторого угла, у которого одна сторона, параллельная плоскости проекции, равна прямому углу, то и проецируемый угол также

7.1 Определение действительной величины плоского угла но его ортогональным проекциям

Решение задачи сводится к перемещению плоскости общего положения, которой принадлежит угол, в положение, параллельное какой- либо плоскости проекции. Такое перемещение можно осуществить с помощью методов преобразования ортогональных проекций.

Наиболее рациональный путь решения задачи по переводу плоскости угла в положение, параллельное плоскости проекции, достигается путем вращения плоскости угла вокруг линии уровня.

В этом случае для получения ответа на поставленную задачу достаточно произвести поворот только одной точки вокруг горизонтали или фронтали плоскости угла.

При использовании других способов преобразования нам пришлось бы дважды менять плоскости проекции либо дважды осуществлять перемещение (вращение), параллельное плоскости проекции, т.е. в обоих случаях потребовалось построение двух вспомогательных проекций,

89

Приведенные ниже примеры иллюстрируют использование способа вращения вокруг линии уровня для решения задачи определения действительной величины плоского угла.

Пример 1: Определить угол между пересекающимися прямыми а и Ь.

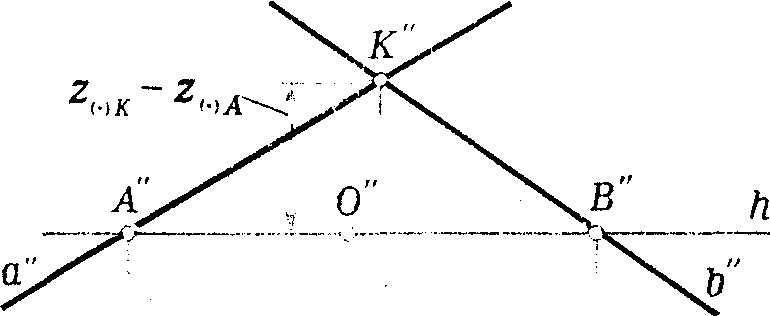
Поворачиваем плоскость (а  b)- вокруг ее горизонтали h в новое положение, параллельное горизонтальной плоскости. Точки А (А э а) и В (Вэ b) принадлежат оси вращения h (A, B)h, поэтому при вращении плоскости а вокруг оси h они не изменяют своего положения.

Следовательно, для определения нового положения плоскости ₁ Н достаточно осуществить поворот только одной точки К. Для этого проводим через К' прямую, перпендикулярную h ( с этой прямой будет совпадать горизонтальная проекция окружности, по которой перемещается точка при ее вращении вокруг горизонтали). Далее определяем положение центра вращения 0 и величину радиуса вращения R для точки К. Положение точки К₁ совместно с А и В определяют новые проекции a'₁ и b₁ (прямых а и b),

90

задающих плоскость ₁ Н. Поэтому А К' В' равен искомому углу °

Пример 2, Определить величину углов треугольника АВС. Повернем плоскость треугольника АВС вокруг фронтали и этого треугольника в положение, параллельное плоскости V. Через вершину А треугольника АВС проводим фронталь u(uu'). Точки А и D, как принадлежащие оси вращения, не изменяет своего положения в процессе преобразования. Поэтому, как и в предыдущем примере, достаточно повернуть только одну точку.

На рис 7.3 в качестве такой точки взята вершина В треугольника АВС. Вершина треугольника С при вращении вокруг фронтали будет перемещаться по дуге окружности, плоскость которой перпендикулярна оси вращения; поэтому фронтальная проекция этой окружности перпендикулярна  и новое положение точки С₁ определяется в точке пересечения этого перпендикуляра с новым положением (B₁ D). После такого поворота плоскость треугольника переведена в положение параллельное фронтальной плоскости V.

Следовательно, на основании свойства о проецировании плоской фигуры, параллельной плоскости проекции ( изложено в п.7) углы при вершинах А"В₁ и C'₁ проецируются в натуральную величину.

Рис.7.3.

91