
Основы высшей математики для инженеров 2009
.pdf
Ю. В. ЛИПОВЦЕВ, О. Н. ТРЕТЬЯКОВА
ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
ДЛЯ ИНЖЕНЕРОВM62
Учебное пособие
Рекомендовано в качестве учебного пособия для студентов высших технических учебных заведений
Мо с к в а
«В у з о в с к а я к н и г а » 2 0 0 9
ББК 22.1я73 Л61
Рекомендовано УМО АРК Российской Федерации в качестве учебного пособия для студентов высших технических учебных заведений
Р е ц е н з е н т ы:
д р физ. мат. наук, проф. А. В. Пантелеев; канд. физ. мат. наук, доц. А. С. Бортаковский
Липовцев Ю. В., Третьякова О. Н.
Л61 Основы высшей математики для инженеров: учеб. пособие / Ю. В. Липовцев, О. Н. Третьякова. — М.: Вузовская книга, 2009. — 484 c.: ил.
ISBN 978 5 9502M620272 8
В учебном пособии приведены основные теоретические положения традиционных курсов высшей математики для инженерных специально стей технических вузов. Наряду с традиционным изложением курсов алгебры, математического анализа и дифференциальных уравнений, в данном пособии при решении ряда задач из этих разделов используются численные методы и примеры их программной реализации. Особенностью пособия является акцент на постановке и решении физических и техниче ских задач, приводящих к задачам математической физики.
Предназначено для студентов технических вузов всех инженерных специальностей.
ББК 22.1я73
|
© Липовцев Ю. В., Третьякова О. Н., 2002 |
|
© ЗАО «Издательское предприятие |
ISBN 978 5 9502 0272 8 |
«Вузовская книга», 2009 |
Математика есть единая симфония бесконечного.
Д. Гильберт
ПРЕДИСЛОВИЕ
В данном учебном пособии представлен достаточно подробный курс лекций по высшей математике, читаемый для студентов техни ческих специальностей вузов. При разработке пособия использованы учебники и учебные пособия, список которых прилагается в конце книги. К числу основных использованных источников следует отнести учебные пособия и учебники Г. М. Фихтенгольца, П. С. Александрова, Д. В. Беклемишева, В. А. Ильина и Э. Г. Позняка, Л. Д. Кудрявцева, Н. С. Пискунова.
По форме и стилю изложения материала пособие написано как конспект лекций. Каждая лекция является отдельным разделом главы. В начале каждой лекцииM62представлен ее план, нумерация формул дается по лекциям, а рисунков — по главам. Для сокращения записи часто встречающихся выражений используются символы: (знак принадлежности), (квантор существования), (квантор всеобщно сти), (знак бесконечности), (знак стремления), например:
x [a, b] — переменная х принадлежит отрезку [a, b];
x [a, b] — переменная х не принадлежит отрезку [a, b];
x — существует некоторая переменная х;x — для любого значения переменной х;
— переменная x стремится к бесконечности.
Вразделах по методам решения дифференциальных уравнений, систем дифференциальных уравнений, рядам Фурье и другим зна чительное внимание уделено возможностям применения современно го компьютера к решению актуальных инженерно технических задач.
Вэтой связи мы заменили некоторые традиционные разделы и включили системы дифференциальных уравнений второго порядка с переменными коэффициентами, показав возможности их эффек тивного решения конечно разностным методом прогонки. Приведе ны Фортран программы численного решения краевых задач.
Вдевятой главе рассмотрены задачи математического анализа, ко торые связаны с исследованием физических процессов и решением дифференциальных уравнений с частными производными. Их обычно
4 |
Предисловие |
относят к избранным главам высшей математики и называют уравне ниями математической физики.
Инженеры и студенты технических вузов как правило испытывают значительные затруднения в поиске руководства по постановке и реше нию задач в этой обширной и важной отрасли прикладной математики. В связи с этим содержание этой главы ориентировано на учебные пла ны по инженерно техническим специальностям. Например, наряду с традиционным разделом по колебаниям струны включены задачи о по перечных колебаниях балки, исследования устойчивости элементов конструкций динамическим методом гидравлического удара в трубах, расчета критической скорости вращения вала, расчета температурных полей и напряжений и др.
Мы надеемся, что пособие будет полезно студентам технических вузов, изучающих курсы: «Математический анализ», «Аналитическая геометрия и линейная алгебра», «Обыкновенные дифференциальные уравнения», «Методы математического моделирования физических процессов».
Мы также выражаем глубокуюM62благодарность рецензентам: докто ру физико математических наук, профессору А. В. Пантелееву и кан дидату физико математических наук, доценту А. С. Бортаковскому, полезные замечания которых были учтены при доработке рукописи.
Авторы

ГЛАВА 1
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ИАНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
1.1.Векторы на плоскости и в пространстве
Определение свободного вектора. Алгебраические операции над век торами. Разложение вектора по базису. Системы координат на плос кости и в пространстве.
Среди величин, изучаемых физикой, механикой и другими (в том числе техническими) науками, выделяются две группы: скалярные ве личины (длина, площадь, масса и др.), значения которых вполне опре деляются одним действительным числом, и векторные (сила, скорость, напряженность и др.), которые в отличие от скалярных характеризуют ся не только указанием числовогоM62значения, но и направлением. Поня тие вектора представляет собой математическую абстракцию физиче ских векторных величин. Математическая дисциплина, в которой изучают свойства операций над векторами, называется векторным ис числением и состоит из векторной алгебры и векторного анализа. Воз никновение и развитие векторного исчисления тесно связано с потреб ностями механики и физики. В его создании приняли участие как математики (Р. Декарт, П. Ферма, У. Гамильтон, М. В. Остроградский), так и физики (Дж. К. Максвелл, Дж. Гиббс и др.)
|
1.1.1. Определение свободного вектора |
|
|
ОПРЕДЕЛЕНИЕ 1. Закрепленным вектором |
|
AB называется направленный отрезок АВ, нача |
|
|
лом которого является точка А, а концом — точка |
|
|
В. Вектор, начало и конец которого совпадают, |
|
|
называется нулевым (pис. 1.1). |
Pис. 1.1 |
|
Расстояние между точками А и В называется длиной (модулем) вектора AB и обозначается | AB |.
ОПРЕДЕЛЕНИЕ 2. Множество всех закрепленных векторов, полу чающихся из фиксированного закрепленного вектора с помощью парал лельного переноса, называется свободным вектором и обозначается a.
6Глава 1. Элементы линейной алгебры и аналитической геометрии
1.1.2.Алгебраические операции над векторами
I. Операция сложения
|
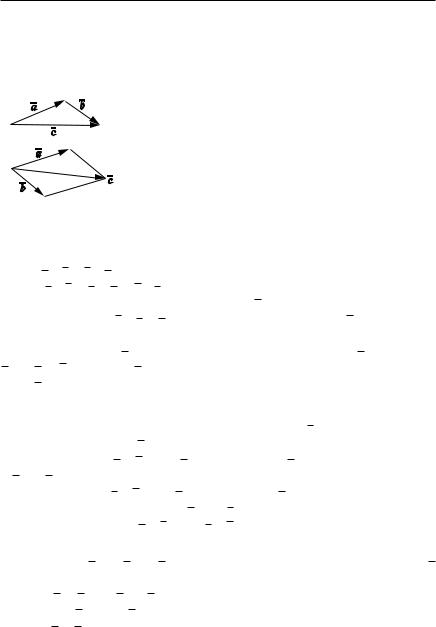
ОПРЕДЕЛЕНИЕ 3. Суммой двух свободных |
||||||||||||||
|
векторов |
|
|
и b называется свободный вектор |
|
, на |
|||||||||
|
a |
c |
|||||||||||||
|
чало которого совпадает с началом первого, а ко |
||||||||||||||
|
нец — с концом второго, если совмещены конец |
||||||||||||||
|
вектора |
|
и начало вектора b (рис. 1.2). |
|
|
||||||||||
|
a |
||||||||||||||
|
З а м е ч а н и е. Легко видеть, что если |
|
и b приведе |
||||||||||||
|
a |
||||||||||||||
|
ны к общему началу, то |
|
|
|
b является диагональю |
||||||||||
|
c |
a |
|||||||||||||
|
параллелограмма, построенного на этих векторах. |
||||||||||||||
|
Это определение согласуется с решением од |
||||||||||||||
|
ной из важнейших задач механики — отысканием |
||||||||||||||
|
равнодействующей системы сил, приложенных в |
||||||||||||||
Pис. 1.2 |
одной точке. |
||||||||||||||
Свойства операции сложения.
1.a b b a (коммутативность).
2.(a b) c a (b c)M6(ассоциативн2ость).
3.Существует единственный вектор 0, называемый нулевым век тором, такой, что 0 a a для всех a. Нулевой вектор 0 порождается нулевым закрепленным вектором, т. е. точкой.
4.Для любого a существует единственный вектор a такой, что a ( a) 0. Вектор a называется вектором, противоположным век тору a.
II. Операция умножения вектора на число
ОПРЕДЕЛЕНИЕ 4. Произведением вектора a на число R на зывается вектор b a такой, что:
1) если 0, a 0, то a получается из a растяжением в раз:
|a| | a|;
2)если 0, a 0, то a получается из a растяжением в | | раз и последующим отражением: | a| | | | a|;
3)если 0 или a 0, то a 0.
Свойства операции умножения.
1.( 1 2)a 1a 2 a для любых действительных 1, 2 и всех a (дистрибутивность).
2.(a1 a2) a1 a2 (дистрибутивность).
3.( 1 2)a 1( 2 a) (ассоциативность).
4.1 a a.
1.1. Векторы на плоскости и в пространстве |
7 |
1.1.3. Разложение вектора по базису
Сначала изучим разложение векторов на плоскости.
ОПРЕДЕЛЕНИЕ 5. Два или более свободных векторов называют ся коллинеарными, если они, отложенные от одной точки, лежат на одной прямой.
Из определения умножения вектора на число вытекает, что векто ры a и b коллинеарны тогда и только тогда, когда существует действи тельное число такое, что
|
a |
b. |
(1) |
ОПРЕДЕЛЕНИЕ 6. Два неколлинеарных вектора на плоскости называются базисом на плоскости.
Теорема 1. Любой вектор c, лежащий на плоскости, можно единст2 венным образом разложить по базису e1, e2 , то есть представить в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||
|
|
|
|
|
|
|
|
|
|
a |
xe1 ye2. |
|
|
|
|
|
||||||||||||
Доказательство. Единственность разложения: предположим про |
||||||||||||||||||||||||||||
Отсюда |
|
|
|
M62 |
|
|
|
|
|
|
|
|||||||||||||||||
тивное, т. е. есть по крайней мере два разложения: |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
a |
x1 |
e1 y1e x2 e1 y e , |
x1 x2. |
|
|
||||||||||||||||||
|
|
|
(x x ) |
|
(y y ) |
|
, |
e |
y2 y1 |
|
|
|
|
. |
||||||||||||||
e |
e |
e |
e |
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
1 |
|
2 1 |
2 |
1 2 |
|
1 |
|
x x |
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
||
В силу (1) |
|
|
|
|
|
|
|
|
||||||||||||||||||||
e1, e2 коллинеарны. Получили проти |
|
|
|
|
||||||||||||||||||||||||
воречие, т. е. представление (2) единственно. |
|
|
|
|
||||||||||||||||||||||||
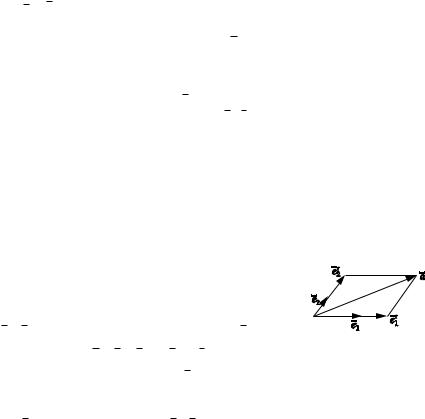
Существование |
разложения (2) |
получается |
|
|
|
|
||||||||||||||||||||||
путем построения параллелограмма на векторах
e1, e2 , диагональю которого является a: |
|
a e1 e2 xe1 ye2. |
Рис. 1.3 |
При разложении вектора a использовались определения сложения векторов и умножения на число.
Числа x, y в разложении (2) называются координатами (x, y) векто ра a относительно базиса e1, e2 .
Рассмотрим теперь пространственный случай.
ОПРЕДЕЛЕНИЕ 7. Три или более свободных векторов называют ся компланарными, если они, отложенные от одной точки, лежат в одной плоскости.
ОПРЕДЕЛЕНИЕ 8. Три некомпланарных вектора в пространстве называются базисом в пространстве.
8Глава 1. Элементы линейной алгебры и аналитической геометрии
Теорема 2. Любой вектор a в пространстве можно единственным способом разложить по базису e1, e2 , e3, т. е. представить в виде
|
|
|
|
|
|
|
|
|
(3) |
a |
xe1 ye2 ze3. |
||||||||
Доказательство аналогично доказательству теоремы 1, только для осуществления разложения необходимо на векторах e1, e2 , e3 построить параллелепипед, диагональю которого является вектор a.
Числа x, y, z в разложении (3) называются координатами вектора a относительно базиса e1, e2 , e3. При этом можно записать
axe1 ye2 ze3 (x, y, z).
1.1.4.Система координат на плоскости и в пространстве
ОПРЕДЕЛЕНИЕ 9. Системой координат на плоскости или в про странстве называется фиксированная точка 0 (начало координат) и ба зис, отложенный от этой Mточки. Прямые,62на которых лежат базисные векторы, называются осями координат. Если оси координат перпен дикулярны, то система координат называется прямоугольной или де картовой.
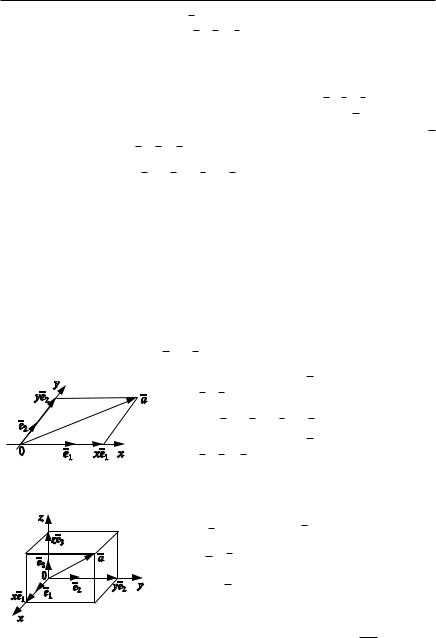
axe1 ye2 (x, y)
—координаты вектора a в системе коорди
нат 0, e1, e2 (pис. 1.4).
|
a xe1 ye2 ze3 (x, y, z) |
|
|
— координаты вектора a в системе коорди |
|
|
нат 0, e1, e2 , e3 (pис. 1.5). |
|
Рис. 1.4 |
При сложении векторов их координаты |
|
складываются, а при умножении вектора на |
||
|
||
|
число координаты умножаются на это число: |
|
|
a (x1, y1, z1), b (x2, y2, z2), |
|
|
a b (x1 x2, y1 y2, z1 z2), |
|
|
a ( x1, y1, z1), R, |
|
|
где R — множество действительных чисел. |
|
|
Координатами точки M(x, y, z) называют |
|
Рис. 1.5 |
ся координаты радиуса вектора 0M (x, y, z). |

1.2. Линейные пространства |
9 |
Итак, нами установлено взаимно однозначное соответствие между векторами или точками на плоскости и парами чисел и между векто рами или точками в пространстве и тройками чисел. Это соответствие является сущностью метода координат, позволяющего геометрические вопросы переводить на алгебраический язык, язык чисел. Этот метод был предложен в XVII в. французским математиком Рене Декартом и явился основой для создания аналитической геометрии.
1.2. Линейные пространства
Определение и примеры линейных пространств. Понятие и свойства линейной зависимости векторов. Размерность и базис. Разложение вектора по базису.
При построении аналитической геометрии Р. Декарт и П. Ферма опирались на геометрию трехмерного пространства Евклида. Практи ка измерений, механика Ньютона, развитие точных наук вплоть до первой половины XIX в. способствовали тому, что ученые и философы считали принципы и теоремыM62геометрии Евклида не только истинны ми, но и единственно возможным и абсолютно точным описанием свойств реального пространства в целом. Открытие неевклидовой гео метрии русским математиком Н. Лобачевским и венгерским матема тиком Бойя, создание Эйнштейном теории относительности, в кото рой подчеркивается четырехмерность реального пространства, показа ли, что абсолютизация геометрии Евклида лишена оснований, что только все геометрические теории могут дать, и действительно дают, все более точное описание свойств пространства в целом. Отвлекаясь от конкретного содержания геометрических векторов, выделяя линей ные операции над ними, немецкие математики Г. Грассман, Д. Гиль берт, Г. Вейль в конце XIX — начале ХХ в. создали понятие линейного пространства, в котором элементы (векторы) могут иметь произволь ную природу.
1.2.1. Определение и примеры линейных пространств
ОПРЕДЕЛЕНИЕ 1. Множество L элементов произвольной приро ды x, y, … называется линейным пространством над полем действи тельных чисел R, если:
а) x, y L поставлен в соответствие элемент z L, называемый суммой элементов x, y. Сумма элементов x, y обозначается че рез x y;

10 Глава 1. Элементы линейной алгебры и аналитической геометрии
б) x L, R поставлен в соответствие элемент x L, назы ваемый произведением числа на элемент x.
Для пояснения сказанного необходимо напомнить, что символи ческая запись « x, y L» означает сокращенную запись выражения «для любых двух векторов x, y, принадлежащих множеству L». Анало гичным образом с помощью символики R записано выражение «для любого , принадлежащего множеству действительных чисел R».
Эти операции должны удовлетворять следующим аксиомам.
I. Аксиомы сложения.
1.x y y x (коммутативность).
2.(x y) z x (y z) (ассоциативность).
3.элемент 0 такой, что x 0 x для любого x L. Элемент 0 на зывается нулевым.
4.x L существует элемент ( x) L, называемый противополож ным, такой, что x ( x) 0.
II. Аксиомы умноженияM62на число.
1. (x y) x y (дистрибутивность). 2. ( )x x x (дистрибутивность). 3. ( )x ( x) (ассоциативность).
4. x x.
Элементы линейного пространства будем называть векторами. Укажем некоторые примеры линейных пространств.
1.L R — множество действительных чисел с обычными опера циями сложения и умножения. Выполнение аксиом сложения и умно жения очевидно.
2.L Rn {x (x1, x2, , xn), xi R} — множество упорядоченных
наборов из n чисел (арифметическое пространство). Положим для x (x1, x2, , xn), y (y1, y2, , yn), R
x y (x1 y1, x2 y2, , xn yn) Rn,
x ( x1, x2, , xn) Rn.
Так как сложение и умножение производится покоординатно по чис лам, то аксиомы сложения и умножения выполнены.
3. L2 — множество свободных векторов на плоскости, L3 — в трех мерном геометрическом пространстве. При этом L2 и L3 являются ли нейными пространствами относительно введенных в них операций.
