
Основы высшей математики для инженеров 2009
.pdf
2.5. Бесконечно малые и бесконечно большие функции |
81 |
П р и м е р 1. |
|
|
|
|
|
|
|
|
|
x2 |
2 x |
|
2 |
|
2 |
|
|
lim |
|
|
lim 1 |
|
|
lim 1 lim |
|
1 0 1. |
|
x2 |
|
|
|||||
x |
|
x |
x |
x x x |
||||
Теорема 2. Предел произведения конечного числа функций равен про2
изведению их пределов: |
|
|
|
|
|
|
|
|||
lim |
f (x) f (x) f |
(x) lim |
f (x) lim |
f (x) lim |
f (x). |
|||||
x a |
1 |
2 |
|
n |
x a |
1 |
x a |
2 |
x a |
n |
Доказательство. Докажем теорему для случая двух сомножителей. |
||||||||||
Пусть lim f1(x) A1, |
lim f2(x) A2, |
тогда |
f1(x) A1 )1(x), f2(x) |
|||||||
A2 )2(x) и f1(x) f2(x) A1A2 A1)2(x) A2)1(x) )1(x))2(x). |
||||||||||
Так как |
A1)2(x) A2)1(x) )1(x))2(x) — бесконечно малая функ |
|||||||||
ция, то |
|
lim |
f (x) f (x) A A lim |
f (x) lim |
f (x). |
|
||||
|
|
|
||||||||
|
|
x a |
1 |
2 |
1 2 |
x a |
1 |
x a |
2 |
|
Следствие. ПостоянныйM62множитель можно выносить за знак пре дела.
П р и м е р.
lim 5x3 5 lim x3 5 8 40.
|
|
|
|
|
|
|
x 2 |
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 3. Предел частного двух функций равен частному их преде2 |
|||||||||||||||||||||||||||||
лов, если предел знаменателя отличен от нуля: |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
f1(x) |
|
|
lim |
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
lim |
|
x a |
1 |
|
|
, |
|
если |
|
lim |
f |
(x) 0. |
|||||||||||||
|
|
|
|
|
f |
(x) |
|||||||||||||||||||||||
|
|
|
|
x a f |
(x) |
lim |
|
|
|
|
|
|
x a |
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
x a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Пусть |
lim f (x) |
A , |
lim |
f |
(x) A . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x a |
1 |
|
|
|
1 |
x a |
2 |
|
|
|
|
2 |
|
||||||
Тогда |
f1(x) A1 )1(x), |
f2(x) A2 )2(x) и |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
f (x) |
|
A ) (x) |
|
|
A |
|
A |
) |
(x) |
A |
|
||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
1 |
|
|
|
|
1 |
|
|||||||
|
|
f2(x) |
A2 )2(x) |
A2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
A2 )2(x) |
A2 |
|||||||||||||||||||||
|
A1 |
|
A2(A1 )1(x)) A1(A2 )2(x)) |
|
A1 |
|
A2)1(x) A1)2(x) |
, |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
A2 |
|
|
|
|
A2(A2 )2(x)) |
|
|
|
|
|
|
A2 |
|
|
|
|
A2(A2 )2(x)) |
|||||||||||
где дробь |
A2)1(x) A1)2(x) |
есть бесконечно малая функция. |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
A2(A2 )2(x)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

82 Глава 2. Дифференциальное исчисление функций одной переменной
Следовательно, |
|
|
|
lim |
f (x) |
||
|
f1(x) |
|
A1 |
|
|||
lim |
|
|
x a |
1 |
. |
||
|
|
|
|
||||
x a f2(x) |
|
A2 |
|
lim |
f2(x) |
||
|
|
|
|
|
x a |
|
|
П р и м е р ы.
1. lim 3x 5 8 4. x 1 4x 2 2
2. lim x2 4 lim (x 2) 4.
|
|
x 2 x 2 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5.3. Бесконечно большие функции |
|
|
|||||||||
|
ОПРЕДЕЛЕНИЕ 1. Функция f (x) называется бесконечно большой |
|||||||||||||
при x , если M 0 |
N 0, что при x N |
| f (x)| M. |
||||||||||||
|
П р и м е р. y x2 — бесконечно большая функция при x . |
|||||||||||||
|
Аналогично определяется бесконечно большая функция при x a. |
|||||||||||||
|
Пишут: lim |
f (x) (lim f (x) ). |
|
|
|
|
|
|
||||||
|
|
x |
|
|
x a |
|
|
|
|
|
|
|||
Если функция f |
(x) |
положительна для всех достаточно больших x, то |
||||||||||||
|
M62 |
|
|
|
|
|
|
|||||||
она стремится к , если отрицательна, то |
lim |
f (x) . |
||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
Связь между бесконечно большими и бесконечно малыми функ |
|||||||||||||
циями устанавливается следующей теоремой. |
|
|
|
|||||||||||
|
Теорема 1. Если функция f (x) — бесконечно большая при x , то |
|||||||||||||
1 |
|
бесконечно малая функция. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Доказательство. Выберем 1 0. Так как функция f (x) — бесконеч |
|||||||||||||
но большая, то N: | f (x)| |
1 |
при x N тогда |
|
1 |
|
|
1 для тех же x, т. е. |
|||||||
|
|
f (x) |
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
1 |
|
— бесконечно малая функция. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Теорема 2. Если f (x) — бесконечно малая функция при x a и не об2 |
|||||||||||||
ращается в нуль при достаточно близких к a x, то |
1 |
— бесконечно |
||||||||||||
|
||||||||||||||
f (x)
большая.
Доказательство теоремы аналогично доказательству теоремы 1.

2.6. Сравнение бесконечно малых |
83 |
2.6. Сравнение бесконечно малых
Сравнение бесконечно малых. Свойства непрерывных в точке функций. Классификация точек разрыва. Свойства функций, непрерывных на отрезке.
2.6.1. Сравнение бесконечно малых
ОПРЕДЕЛЕНИЕ 1. Если отношение бесконечно малых функций *
)
имеет конечный и отличный от нуля предел, то * и ) называются беско нечно малыми одного порядка. Символически это записывается сле дующим образом: ) O4*5.
П р и м е р. ) x, * 3x, (x 0); ) O(*). |
|
|
|
|||
|
* |
|
|
) |
|
|
ОПРЕДЕЛЕНИЕ 2. Если lim |
|
0 lim |
|
, то * |
называется |
|
|
|
|||||
|
) |
|
|
* |
|
|
M62— |
: * o()). |
|
||||
бесконечно малой высшего порядка, чем ) |
|
|||||
П р и м е р. * x, ) x3 (x 0).
ОПРЕДЕЛЕНИЕ 3. Функция * называется бесконечно малой k го
порядка относительно ), если * и )k |
бесконечно малые одного по |
|||||
* |
A 0.. |
|
|
|
||
рядка, т. е. lim |
|
|
|
|
||
)k |
|
|
|
|||
П р и м е р. ) x, * x3, x 0.. |
|
|
||||
|
|
lim |
* |
lim |
x3 |
1. |
|
|
|
|
|||
|
|
x 0 )3 |
x 0 x3 |
|
||
ОПРЕДЕЛЕНИЕ 4. Если lim * 1, то бесконечно малые ) и * эк
)
вивалентны: ) ~ *.
П р и м е р. x ~ sin x, x ~ tg x, x ~ ln (1 x).
Теорема. Пусть ) ~ )1, * ~ *1, тогда
lim ) lim )1 .
x a * x a *1

84 Глава 2. Дифференциальное исчисление функций одной переменной
Доказательство. Представим отношение ) в следующем виде:
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
) |
|
) *1 )1 |
; |
lim |
) |
1, |
lim |
*1 |
1 lim |
) |
lim |
)1 |
. |
|
|
|
|
|
|
||||||||
* * )1 *1 |
)1 |
|
* |
* |
*1 |
|
|||||||
Таким образом, при вычислении пределов бесконечно малые можно заменять эквивалентными.
П р и м е р ы. |
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
|
|
|
|
sin 3x |
|
3x |
|
|
1 cos x |
|
|
|
|
1 |
|
||
lim |
lim |
3; |
lim |
lim |
2 |
|
. |
|||||||
|
|
|
x2 |
|
||||||||||
x 0 x |
x 0 x |
x 0 |
x2 |
x 0 |
2 |
|
||||||||
|
2.6.2. Свойства функций, непрерывных в точке |
|
|
|
||||||||||
Напомним: функция f (x) непрерывна в точке x0, если |
||||||||||||||
|
|
lim f (x) f (x0) или |
lim |
-y 0. |
|
|
|
|||||||
|
|
x x0 |
|
|
-x 0 |
|
|
|
|
|
|
|||
Из основных теорем о пределахM62вытекают следующие теоремы о свой ствах непрерывных функций.
Теорема 1. Если f (x) и ((x) непрерывны в точке x a, то в этой точ2 ке непрерывны их сумма, разность, произведение и частное (при ((a) 0).
В самом деле, в рассматриваемом случае
f (a) lim f (x), |
((a) lim ((x). |
x a |
x a |
Теорема 2. Пусть задана функция |
f (u), непрерывная в точке u A, |
и функция u ((x), непрерывная в точке x a, и пусть ((a) A. Тогда сложная функция F(x) f (((x)) непрерывна в точке x a.
Доказательство. Функция f (x) непрерывна в A, следовательно, оп ределена в некоторой окрестности этой точки. Поэтому
lim F(x) lim |
f (((x)) lim f (u) f (A) f (((a)) F(a). |
|
x a |
x a |
u A |
Здесь u ((x) и учтена непрерывность функции ( в точке x a:
((x) ((a) A.
x a
П р и м е р ы.
1) P(x) a0 xn a1xn 1 an непрерывна x;

|
|
|
|
|
2.6. Сравнение бесконечно малых |
85 |
||||||
|
|
|
' |
|
' |
|
|
|||||
2) |
y cos x |
sin |
|
x , где u |
|
x — непрерывна; |
|
|||||
|
|
|
||||||||||
|
|
|
2 |
|
2 |
|
|
|||||
3) |
y tg x |
sin x |
, |
x |
' |
'k, |
k 0, /1, ; |
|
||||
|
|
|
||||||||||
|
|
|
cos x |
2 |
|
|
|
|
|
|||
4) |
y sin3 x5. |
|
|
|
|
|
|
|
||||
Из свойств предела функции следует также теорема:
Теорема 3. Если функция f (x) непрерывна в точке a, то существует окрестность u(a) этой точки, на которой f (x) ограничена.
2.6.3. Классификация точек разрыва
Рассмотрим различные случаи предельного перехода к точке х0 слева и справа:
|
x x0 0, |
|
|
x x0 0 |
x x0 0. |
|
|
xM62x0 0 x x0 |
|
||
Для непрерывной в точке x0 |
функции имеют место следующие ра |
||
венства: |
|
|
(1) |
lim |
f (x) lim |
f (x) lim f (x) f (x0). |
|
Если функция такова, что для нее существуют конечные пределы
lim f (x), |
lim f (x), |
x x0 0 |
x x0 0 |
но равенства (1) не выполняются, то, очевидно, f (x) разрывна в точке x0. В этом случае говорят, что f (x) имеет в точке x0 разрыв 1 го рода.
Если lim |
f (x) lim f (x) f (x0), то x0 — точка устранимого |
x x0 0 |
x x0 0 |
разрыва.
Если у функции f (x) не существует правостороннего или левосто роннего предела в точке x0, или эти пределы равны , то говорят
о разрыве 2 го рода. |
|
||||
П р и м е р ы. |
|
|
|
|
|
|
x sin |
1 |
, |
x 0, |
|
|
|
||||
1) |
& |
|
x |
|
|
f (x) |
|
|
|||
|
& |
0, |
|
|
x 0; |
|
|
|
|
||

86 |
Глава 2. Дифференциальное исчисление функций одной переменной |
|||
|
1 |
, |
x 0, |
|
2) |
& |
|
||
|
|
|
||
f (x) x |
|
|
||
|
& |
|
|
x 0. |
|
2, |
|||
2.6.4. Свойства функций, непрерывных на отрезке
Функция f (x) называется непрерывной на отрезке [a, b], если она непрерывна во всех точках (a, b), а в точке a непрерывна справа, в точке b — слева.
Теорема 1. Если функция f (x) непрерывна на [a, b], то она ограничена
на нем, т. е. k 0: | f (x)| k x [a, b].
Теорема 2 (Вейерштрасса). Если функция f (x) определена и непрерыв2
на на [a, b], то она достигает в этом промежутке своих точных верхней
и нижней границ, т. е. существуют |
точки |
), * [a, b] |
такие, что |
||||
f ()) f (x) f (*) |
или |
M62 |
f (x) f (*). По теореме 1 |
||||
inf |
f (x) f ()), |
sup |
|||||
|
|
x [a, b] |
|
x [a, b] |
|
|
|
f (x) ограничена. |
Следовательно, существуют |
конечные |
inf и sup: |
||||
inf f (x) sup f (x).
Теорема 3. Если f (x) определена и непрерывна на [a, b] и числа f (a) и f (b) отличны от нуля и имеют разные знаки, то на (a, b) имеется, по крайней мере, одна точка С такая, что f (c) 0.
Рис. 2.10 |
Рис. 2.11 |
Следствие. Если f (x) непрерывна на [a, b], f (a) A, f (b) B (A B) и
A C B, то c: f (c) C, т. е. непрерывная на [a, b] функция принимает все промежуточные значения между ее значениями на концах [a, b].
Доказательство. F(x) f (x) C непрерывна на [a, b], f (a) C 0; f (b) C 0 c: f (c) C 0 f (c) C.

2.7. Введение в дифференциальное исчисление функций одной переменной… 87
2.7. Введение в дифференциальное исчисление функций одной переменной. Производная
Производная, ее геометрический смысл. Механический смысл произ водной. Дифференцируемость и ее связь с непрерывностью. Произ водные элементарных функций.
Дифференциальное исчисление — раздел математики, в котором изучаются понятия производной и дифференциала и способы их при менения к исследованию функций. Развитие дифференциального ис числения тесно связано с развитием интегрального исчисления. Вме сте они составляют основу математического анализа, имеющего чрез вычайное значение для естествознания и техники. В общих чертах построение дифференциального и интегрального исчислений было за ложено в трудах механиков И. Ньютона и Г. Лейбница во второй по ловине XVII века. Имя и труды выдающегося английского ученого Исаака Ньютона (1643–1727), заложившего основы современного ес тествознания и классической физики, широко известны. Немецкий ученый Готфрид ВильгельмM62Лейбниц (1646–1716) независимо от И. Ньютона начал разработку дифференциального и интегрального исчисления при проведении научных исследований, которые относят ся к механике, теории упругости и теории колебаний. Создание диф ференциального исчисления явилось началом периода бурного разви тия математики и связанных с ними прикладных наук.
Дифференциальное исчисление основано на понятиях действи тельного числа, функции, предела и непрерывности — важнейших по нятиях математики, с которыми мы познакомились на предыдущих лекциях.
Основные понятия дифференциального исчисления — производ ная и дифференциал — и разработанный в дифференциальном исчис лении аппарат, связанный с ними, доставляют средства для исследова ния функций.
2.7.1. Производная
Производной от функции f (x) в точке x называется предел отно шения ее приращения -y в этой точке к соответствующему прираще нию аргумента -x, когда -x 0:
f (x) lim |
-y |
lim |
f (x -x) f (x) |
. |
(1) |
|
|
||||
-x 0 -x |
-x 0 |
-x |
|
||
88 Глава 2. Дифференциальное исчисление функций одной переменной
О б о з н а ч е н и я: dy, y , df (x). dx dx
Для одной и той же функции производные можно вычислять в разных точках. В каждой точке x, для которой существует предел (1), f (x) определяется как предел. Процесс нахождения производных — дифференцирование.
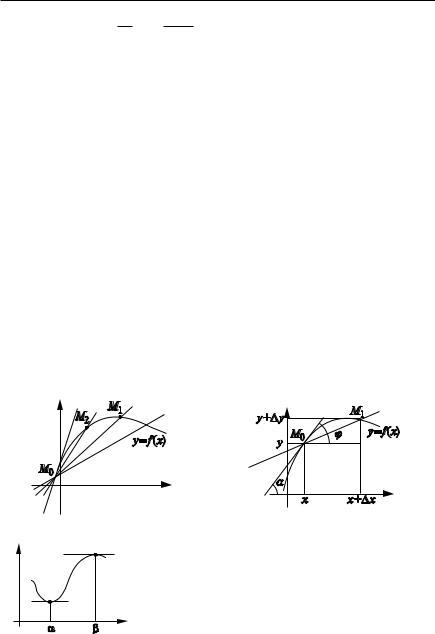
Геометрический смысл производной. Пусть M0 — фиксированная точка, M0M1, M0M2 — секущие. Если M1 M0 по кривой, то секущая занимает различные положения: M0M1, M0M2 . Предельное положение секущей, когда M1 M0 (с любой стороны), называется касательной
к кривой в точке M0 (рис. 2.12). |
|
|
|
|
|
|||
Пусть |
точка M0 имеет координаты x, |
y, |
M1 — |
x -x, y -y, |
||||
y -y f (x -x). Имеем: tg ( |
-y |
. Если -x 0, |
то M |
M |
0 |
и угол ( |
||
|
||||||||
|
|
-x |
|
1 |
|
|
||
|
|
|
|
|
|
|
||
меняется. Если 6( 6), то прямая, проходящая через M0 и состав |
||||||||
ляющая 6) с осью OX, и будет касательной. При этом |
|
|
||||||
|
tg ) lim tg ( lim -y f (x). |
|
|
|
||||
|
-x 0 |
|
-x 0 -x |
|
|
|
|
|
Итак, |
) tg ). Таким образом, значение производной f (x) в |
|||||||
точке x естьf (xтангенс угла,M6который образует2 |
касательная к графику |
|||||||
функции в данной точке M [x, |
f (x)] с положительным направлением |
|||||||
оси OX (рис. 2.13). |
|
|
|
|
|
|
|
|
Рис. 2.12 |
Рис. 2.13 |
Если tg ) 0, то касательная в точках x ), x * параллельна оси OX.
Рис. 2.14

2.7. Введение в дифференциальное исчисление функций одной переменной… 89
2.7.2. Механический смысл производной
Пусть материальная точка движется прямолинейно по закону S f (t), где t — время, S — путь. Пусть t t0. Найдем скорость точки при t t0. Рассмотрим t0 -t. Тогда S (t0 -t) f (t0 -t),
vcp f (t0 -t) f (t0) -S .
-t -t
Если -t меняется, то vcp — функция от t. Скоростью v0 в данный мо мент t0 называется предел средней скорости vcp при -t 0, т. е.
v0 lim |
-S |
|
lim |
f (t0 -t) f (t0) |
f (t). |
|
|
||||
-t 0 -t |
-t 0 |
-t |
|||
Таким образом, механический смысл производной заключается в сле дующем: производная функции f (x) в данной точке x0 есть скорость изменения функции в данной точке.
2.7.3M62. Дифференцируемость
ОПРЕДЕЛЕНИЕ. Функция, имеющая производную в точке x x0, называется дифференцируемой в этой точке. Если существует произ водная f (x) во всех точках [a, b], то функция называется дифферен цируемой на [a, b].
Теорема. Если y f (x) дифференцируема в некоторой точке x x0, то она непрерывна в этой точке.
Доказательство. В соответствии с определением непрерывности,
достаточно показать, что |
lim |
-y 0. |
|
|||||
|
|
|
|
-x 0 |
|
|||
Имеем -y |
-y |
-x; |
lim -y |
lim |
-y |
lim -x f (x ) 0 0. |
||
|
|
|||||||
|
-x |
-x 0 |
-x 0 -x |
0 |
||||
|
-x 0 |
|||||||
Из теоремы следует, что в точках разрыва функция не может иметь производной. Обратное неверно.
lim | x | |
lim | x | 0. |
x 0 0 |
x 0 0 |
Рис. 2.15 |

90 Глава 2. Дифференциальное исчисление функций одной переменной
Покажем, что при x 0 y | x | не имеет производной: -x x x0 x.
|
lim |
-y |
lim |
| x | |
1; |
||
|
|
||||||
|
-x 0 0 -x |
x 0 0 x |
|||||
lim |
-y |
1, |
следовательно, lim |
-y |
|||
|
|
||||||
-x 0 0 -x |
|
|
|
-x 0 -x |
|||
не существует, и следовательно, функция y | x | не имеет касательной в точке x 0.
|
2.7.4. Производные элементарных функций |
|||
1. C 0. |
|
|
|
|
y C; |
x -x y -y C; |
C lim |
C C |
0. |
|
||||
|
|
-x 0 |
-x |
|
2. (xn) nxn 1. |
|
|
|
|
|||
y xn (n — целое |
число), |
|
|
|
|||
тогда |
|
|
M |
6n(n 21) |
|
||
(x -x)n xn |
1 7 |
|
|||||
|
|
|
9xn nxn 1-x |
xn |
2 -x2 |
||
|
|
||||||
-x |
-x 8 |
|
|
2! |
|
||
-xn xn:<
;
|
n 1 |
|
n(n 1) |
|
n 2 |
|
|
|
|
|
-xn |
|
|
|
n 1 |
||||||||
nx |
|
|
|
|
|
|
|
|
x |
|
|
|
-x |
|
|
nx |
. |
||||||
|
|
|
2! |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-x -x 0 |
|
||||||
Для дальнейшего покажем, что справедливы формулы |
|||||||||||||||||||||||
|
|
|
|
|
|
|
(u / v) u / v , |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
(uv) uv u v, |
|
|
|
|
||||||||||||
|
|
|
|
|
u |
|
u v uv |
|
|
(v 0). |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Имеем -x x -x u -u, |
|
v -v; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
-(u / v) [(u / -u) / (v -v)] (u / v) -u / -v; |
|||||||||||||||||||||||
(u / v) |
lim |
-(u / v) |
|
lim |
|
|
-u |
/ lim |
|
-v |
u / v . |
||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
-x 0 |
|
-x |
|
|
|
|
-x 0 -x -x 0 -x |
|
|||||||||||||
(2)
(3)
(4)
