Основы высшей математики для инженеров 2009

Таким образом, вторая производная вектор функции равна уско рению движения материальной точки в данный момент времени t. В этом заключается механический смысл второй производной.

4.9. Геометрический смысл полного дифференциала

Уравнения касательной прямой и нормальной плоскости к пространст венной кривой. Касательная плоскость и нормаль к поверхности. Гео метрический смысл полного дифференциала функции двух переменных.

4.9.1.Уравнения касательной прямой и нормальной плоскости

кпространственной кривой

На предыдущей лекции было показано, что вектор r(t) направлен по касательной к годографу радиуса вектора OM r(t). Пусть про странственная кривая задана параметрическими уравнениями x ((t), y >(t), z K(t).

Найдем уравнения касательной к этой кривой в некоторой ее точ ке M0(x0, y0, z0), соответствующей параметру t t0.

где m, n, p — проекции направляющего вектора прямой. Так как век тор r (t0) ((t0)i > (t0)j K(t0)k направлен по касательной к кривой в точке M0, то его проекции могут быть приняты за проекции направ ляющего вектора. Тогда искомые уравнения примут вид

x x0 y y0 z z0 .

((t0) > (t0) K(t0)

Нормальной плоскостью к пространственной кривой называется плоскость, перпендикулярная к касательной прямой и проходящая че рез точку касания.

Пусть M0(x0, y0, z0) — точка касания. Уравнение плоскости, прохо дящей через точку M0, имеет вид

A(x x0) B(y y0) C(z z0) 0,

где А, В, С — проекции нормального вектора N (A, B, C) этой плоско сти. Из определения нормальной плоскости следует, что за вектор N

234 Глава 4. Дифференциальное исчисление функций многих переменных

можно принять вектор r (t0) (( (t0), > (t0), K(t0)). Поэтому уравнение нормальной плоскости имеет вид

((t0)(x x0) > (t0)(y y0) K(t0)(z z0) 0.

П р и м е р. Найти уравнения касательной прямой и нормальной

— уравнение нормальной плоскости.

4.9.2. Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности в точке M0 (точке касания) называется плоскость, в которой лежат все касательные в точке M0 к различным кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется перпендикуляр к касатель ной плоскости в точке касания.

Уравнение плоскости имеет вид

A(x x0) B(y y0) C(z z0) 0,

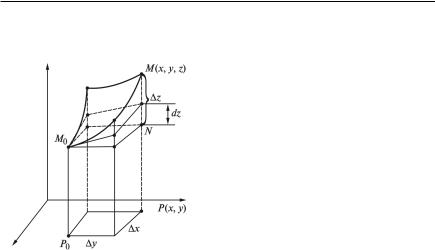
где вектор с координатами А, В, С перпендикулярен плоскости. Пусть поверхность задана уравнением z f (x, y); M0(x0, y0, z0) —

точка, лежащая на ней. Рассмотрим линию L, лежащую на поверхно сти и проходящую через точку M0(x0, y0, z0). Ее параметрические урав нения x x(t), y y(t), z z(t) причем x0 x(t0), y0 y(t0), z0 z(t0).

Так как точка M0 принадлежит поверхности, то z0 f (x0, y0) 0. Про дифференцируем равенство (1) по t:

HF x (t) HF y (t) HF z (t) 0.

Hx Hy Hz

При t t0 получим

Fx(x0, y0, z0) x (t0) Fy(x0, y0, z0) y (t0) Fz(x0, y0, z0) z (t0) 0.

Отсюда следует, что вектор

r (t0) x (t0) i y (t0) j z (t0) k

перпендикулярен вектору с координатами Fx, Fy, Fz. Но вектор r (t0) направлен по касательной к линии L в точке M0. Следовательно, в ка честве нормального вектора к касательной плоскости можно взять вектор с координатами Fx, Fy, Fz. Заметим, что

Поэтому уравнение касательной плоскости имеет вид z z0 fx(x0, y0)(x x0) fy(x0, y0)(y y0).

Вектор { fx, fy,1} направлен по нормали к поверхности, следова тельно, он перпендикулярен к касательной прямой, проведенной к поверхности в точке M0, поэтому уравнения нормали в точке M0 име ют вид

4.9.3. Геометрический смысл полного дифференциала функции двух переменных

Пусть функция z f (x, y) имеет в точке P0(x0, y0) дифференциал

236 Глава 4. Дифференциальное исчисление функций многих переменных

Рассмотрим уравнение касательной плоскости

(Мы обозначили через Z аппликату точки касательной плоскости, чтобы отличить ее от аппликаты z точки по верхности.) Мы видим, что правая часть этого уравнения совпадает с правой частью выражения (2) для дифференциала dz. Следовательно, и левые части этих равенств равны. Но в равенстве (2) левая часть есть диф ференциал функции z f (x, y) в точке P0(x0, y0), а в уравнении (3) левая часть есть приращение аппликаты ка сательной плоскости.

Таким образом, геометрический смысл дифференциала функции двух переменных заключаетсяM62в следующем: дифференциал функ ции двух переменных равен приращению аппликаты касательной плоскости.

238 Глава 5. Интегральное исчисление функций многих переменных

Так как функция f)(x, ) B-)) непрерывна в замкнутой области, то

f)(x, ) B-)) f (x, )) 1,

где 1 — величина, зависящая от x, ), -), стремится к 0 при -) 0. Таким образом,

Переходя к пределу в обеих частях последнего равенства при -) 0, получим

Последняя формула носит название формулы Лейбница. Предположим теперь, что в интеграле не только подынтегральная

функция, но и пределы интегрированияM62зависят от ):

b())

J()) ([), a()), b())] D f (x, ))dx.

a())

Функция ([), a()), b())] является сложной функцией ). Поэтому для вычисления ее производной применим правило дифференцирова ния сложной функции:

Так как производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функ ции, в которую вместо переменной интегрирования подставлено зна чение верхнего предела, то