
Основы высшей математики для инженеров 2009
.pdf
2.17. Комплексные числа |
131 |
Возведение комплексного числа в степень и извлечение корня из комплексного числа. Пусть требуется возвести комплексное число z a bi в степень n. Представим z в тригонометрической форме: z r(cos ( i sin (). По формуле (2)
z n rn(cos n( i sin ()
— формула Муавра.
Корнем n й степени из комплексного числа z называется такое комплексное число, n я степень которого равна z.
Пусть z r(cos ( i sin (). |
|
|
|
|
|
|
|
||||||||||||
|
n |
|
n |
|
|
|
|
|
+(cos > i sin >); |
|
|
||||||||
|
z |
r(cos ( i sin () |
|
|
|||||||||||||||
|
|
|
+n(cos n> i sin n>) r(cos ( i sin (). |
|
|
|
|||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ n |
|
, |
|
|
|
|
n> ( 2'k; |
|
|
|
|
|
||||
|
|
|
r |
|
|
|
|
|
|
|
|
||||||||
|
|
|
> |
( 2'k |
, |
k |
0, 1, , , n 1. |
|
|
|
|||||||||
|
|
|
|
|
|
|
<. |
||||||||||||
|
r(cos i sin |
)Mr cos629 i sin |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Окончательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7( 'k |
( 2 |
'k : |
||||
n |
|
|
|
|
|
|
|
|
|
n |
|||||||||
|
( |
( |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
n |
|
|
; |
||
П р и м е р. Найти все значения кубического корня из 1.
2.17.4. Показательная функция в комплексной области
По аналогии с показательной функцией действительного перемен
ного рассмотрим функцию w ez, где z x iy. По определению, |
|
|||||
|
|
|
|
|
ex iy ex(cos y i sin y). |
(3) |
Пользуясь определением функции ez, можно доказать справедли |
||||||
вость следующих ее свойств. |
|
|||||
1. |
ez1 z2 ez1 ez2. |
|
||||
|
z |
z |
|
ez |
|
|
2. |
e 1 |
|
2 |
1 |
. |
|
|
|
|
||||
|
|
|
|
ez2 |
|
|
3. |
(ez)m emz. |
|
||||
4. |
ez 2'i ez. |
|
||||

132 Глава 2. Дифференциальное исчисление функций одной переменной
Действительно, |
|
|
ez 2'i ez e2'i |
ez e0(cos2' i sin 2') ez. |
|
Полагая в формуле (3) x 0, получим |
|
|
eiy |
cos y i sin y. |
(4) |
(4) — формула Эйлера. |
|
|
2.17.5. Некоторые сведения о многочленах
Многочленом n й степени с действительными коэффициентами называется выражение вида
P(x) A0 xn a1xn 1 an 1x an.
Корнем многочлена называется всякое число ), действительное или комплексное, обращающееM62многочлен в 0, т. е. P()) 0.
При использовании основной теоремы алгебры легко доказывается следующая теорема.
Теорема 1. Всякий многочлен n2й степени может быть представлен в виде произведения коэффициента при старшей степени и n линейных со2 множителей вида x ):
P(x) A0(x )1)(x )2) (x )n).
Числа )i являются корнями многочлена. Таким образом, каждый многочлен имеет ровно n корней, если каждый корень считать столь ко раз, какова его кратность.
Теорема 2. Если коэффициенты многочлена действительны, то вме2 сте с комплексным корнем a bi он имеет и сопряженный корень a bi.
Пусть в разложении есть множитель [x (a bi)]k , и множитель [x (a bi)]k . Перемножив их, получим
{[x (a bi)][x (a bi)]}k [x2 2ax b2 a2]k (x2 px q)k.
Таким образом, произведение линейных множителей, соответствую щих комплексно сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами.
2.17. Комплексные числа |
133 |
Итак, для любого действительного многочлена можно получить разложение
P(x) A0(x x1)k1(x x2)k2 (x2 p1x q1)m1(x2 p2 x q2)m2 ,
где k1 k2 2(m1 m2 ) n.
2.18. Приближенное решение уравнений
Метод хорд. Метод касательных (метод Ньютона). Комбинированный метод. Метод итераций.
Пусть требуется найти действительные корни уравнения f (x) 0, т. е. такие действительные значения x, при которых f (x) обращает ся в 0. Будем считать, что f (x) непрерывна и имеет первую и вторую производные.
Нахождение корней уравнения состоит из двух этапов: 1) отделение корней графическим методом; 2) уточнение найденных значений.
Для отделения корней применяют один из следующих приемов.
M62
Либо строят график функции и тогда точки пересечения графика
с осью ОХ дадут приближенные значения корней, либо преобразуют уравнение к виду f1(x) f2(x) так, чтобы графики функций y f1(x) и y f2(x) легко строились. Абсциссы точек пересечения этих графиков дадут приближенные значения корней.
Для уточнения найденных значений применяются различные методы.
2.18.1. Метод хорд
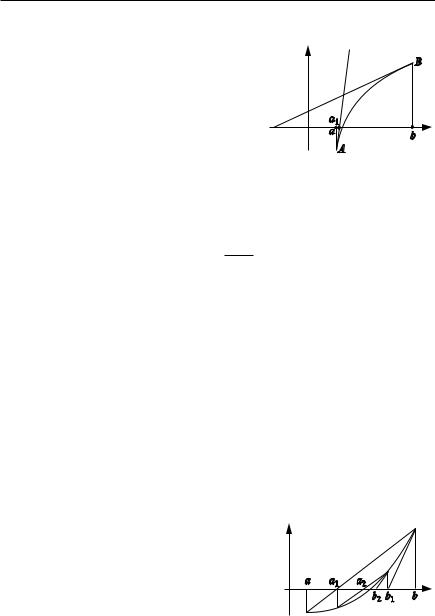
Пусть графическим методом найдено, что корень уравнения нахо дится на отрезке [a, b] (рис. 2.39). Отрезок будем считать столь малым, что на нем выполнены условия:
1)на концах отрезка функция принимает значения разных знаков;
2)f (x) сохраняет знак на [a, b];
3)f (x) сохраняет знак на [a, b].
При этом график функции имеет один из видов, показанных на рис. 2.39.

134 Глава 2. Дифференциальное исчисление функций одной переменной
Рис. 2.39
Метод хорд состоит в следующем. Проведем хорду АВ и найдем абсциссу точки ее пересечения с осью ОХ. Для этого составим уравне ние прямой АВ:
|
x a |
|
y f (a) |
|
или |
x b |
|
y f (b) |
. |
|
||
|
|
|
|
|
|
|||||||
|
b a |
f (b) f |
(a) |
a b f |
(a) f (b) |
|
||||||
При y 0 найдем: |
M62 |
|
|
|
|
|||||||
x a f (a) |
b a |
|
|
или |
x b f (b) |
a b |
. |
|||||
|
|
|
f (a) f (b) |
|||||||||
|
|
|
f (b) f (a) |
|
|
|
|
|||||
Найденное значение х является приближенным значением иско |
||||||||||||
мого корня, обозначим его через х1. Поскольку |
f (x1) не равно нулю, то |
|||||||||||
для вычисления следующего приближения x2 нужно повторить вычис ления, заменив отрезок [a, b] на [a1, b1] следующим образом:
если знак |
f (x1) такой же, как и знак |
f (b) (если |
f (x1) f (b) 0), то |
а1 а, b1 b; |
|
|
|
если знак |
f (x1) противоположен знаку |
f (b) (если |
f (x1) f (b) 0), то |
a1 x1, b1 b.
Вычисления новых приближений прекращаются, когда вновь най денное приближение отличается от предыдущего на достаточно малую величину
 хn xn 1
хn xn 1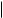 1,
1,
где 1 — заданная точность вычисления искомого корня.
2.18. Приближенное решение уравнений |
|
135 |
|
2.18.2. Метод касательных (метод Ньютона) |
|
||
Если искомый корень находится на от |
|
|
|
резке [a, b] и f (a) 0, а функция |
f (x) на дан |
|
|
ном отрезке выпуклая, т. е. |
f (x) 0 на |
|
|
[a, b], рис. 2.40, то для вычисления первого |
|
|
|
приближенного значения корня х1 прове |
|
|
|
дем касательную к графику функции в точ |
|
|
|
ке а. Пересечение этой касательной с осью |
|
|
|
ОХ дает приближенное значение корня (х1). |
Рис. 2.40 |
|
|
Чтобы найти точку х1, напишем уравнение |
|
||
|
|
||
касательной к графику функции в точке с |
|
|
|
координатами (a, f (a)): |
|
|
|
y f (a) f (a)(x a). |
|
|
|
При y 0 имеем |
a f (a) . |
|
|
х |
|
|
|
1 |
f (a) |
|
|
|
|
|
|
Как видно из приведенногоM62на рис. .40 графика, при таком вы числении приближенного значения корня мы последовательно при ближаемся к корню слева. Поэтому для следующего приближения
вместо а задаем а1 х1.
Проведя теперь касательную в точке A1(a1, f (a1)), получим новое приближение корня. Повторяя этот процесс несколько раз, мы полу чим корень с любой степенью точности.
Заметим, что если бы касательная была проведена не в точке A, а в точке B, то она могла бы пересечь ось абсцисс в точке, лежащей вне отрезка [a, b]. Таким образом, касательную нужно проводить в том конце дуги, в котором знаки функции и ее второй производной сов падают.
2.18.3. Комбинированный метод
Для ускорения процесса отыскания кор ня применяют комбинированный метод хорд и касательных. Пусть f (а) f (b) 0, а f (x) и f (x) сохраняют постоянные знаки на отрезке [a, b], причем f (x) 0; f (x) 0, рис. 2.41. Заметим, что к данному случаю можно свести все другие, если заменить уравнение f (x) 0 равносильным ему урав нением f (x) 0 или / f (z) 0, где z х.
Рис. 2.41 |

136 Глава 2. Дифференциальное исчисление функций одной переменной
Как следует из приведенного графика, в данном случае методом хорд последовательно вычисляются xn с избытком. Поэтому при каж дом переходе к следующему (n 1) му этапу вычисления задаются но вые границы отрезка an xn, bn xn. Найдем первое приближение по методу хорд и по методу касательных:
a1 a f (a) |
b a |
, |
||
f (b) f (a) |
||||
|
|
|||
b b |
f (b) |
. |
|
|
|
|
|||
1 |
f (b) |
|
||
|
|
|||
К отрезку [a1, b1] вновь применим метод хорд и метод касательных. И т. д. Будем получать приближения корня слева и справа по фор мулам
|
|
|
|
|
bn 1 an 1 |
||||
|
an an 1 f (an a) |
|
|
|
|
, |
|||
|
f (b |
f (a |
) |
||||||
|
|
|
|
|
n 1 |
|
|
n 1 |
|
|
b b |
|
f (bn 1) |
. |
|
|
|||
|
|
|
|
||||||
|
n |
n 1 |
|
|
f (bn 1) |
|
|
||
|
|
|
|
|
|
|
|||
При любом n корень уравнения |
f (x) 0 содержится между an и bn. |
||||||||
Пусть x x |
— истинное значение корня. Очевидно, |
||||||||
0 |
M62| x0 an| | an bn|, |
|
|
||||||
| x0 bn| | an bn|.
Таким образом, погрешность не превышает разности между прибли жениями корня слева и справа.
Если задана точность 1, с которой нужно вычислить корень x0, то вычисления проводят до тех пор, пока разность | an bn| не будет мень
ше 1. После этого принимают x0 = an bn . 2
2.18.4. Метод итераций
Пусть корень уравнения f (x) 0 отделен и находится на отрезке [a, b], причем этот отрезок достаточно мал. Предположим, что уравне
ние |
f (x) 0 удалось переписать в виде f1(x) f2(x), причем функция |
f1(x) |
такова, что корень уравнения f1(x) m может быть найден с |
большой степенью точности. Вычисление корня уравнения f (x) 0 тогда проводится следующим образом. Берем x x0 [a, b], вычисляем f2(x0) и находим x1 как решение уравнения
f1(x) f2(x).
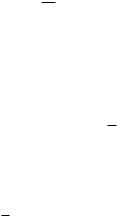
2.18. Приближенное решение уравнений |
137 |
||
Далее: x2 находим как решение уравнения |
f1(x) f2(x1) и т. д. |
||
|
f1(xn) f2(xn 1). |
|
|
Особенно удобно представлять уравнение в виде |
|
||
|
x f2(x). |
|
|
Тогда последовательные приближения находятся по формулам |
|||
x1 f2(x0), |
x2 f2(x1), , |
xn f2(xn 1). |
|
Можно показать, что |
последовательные |
приближения |
сходятся |
к корню A уравнения (xn A) если на выбранном промежутке [a, b] выполнено условие: | f2(x)| q 1.
Укажем способ выбора функции f2(x). Заменим уравнение f (x) 0
эквивалентным уравнением
x x f (x),
d [x f (x)] была малой по абсо dx
лютной величине на [a, b] (b a достаточно мало). Например, можно находить из условия 1 M62f (x0), где x0 — первое приближение корня.
П р и м е р. Привести уравнение x ln x 4 0 при начальном при ближении корня x0 2,5 к виду, удобному для применения метода итераций.
Решение. Здесь f (x) 2 x ln x 4, f (x) 2 1 . Перепишем уравне x
ние в эквивалентном виде:
x x (2 x ln x 4).
Вычисляем производную правой части и приравниваем ее к нулю при
x 2,5, тогда 0,5 и x 2 1 ln x. 2
2.18.5. Фортран>программа вычисления корней заданного уравнения на заданном отрезке
Современный компьютер предоставляет нам чрезвычайно боль шие вычислительные возможности. Поэтому актуальность всех изло женных выше методов решения трансцендентных уравнений снизи лась и уходит в прошлое. Используются они теперь, если требуется найти нужное решение быстро (хотя бы приближенно) с помощью калькулятора.

138 Глава 2. Дифференциальное исчисление функций одной переменной
Если функция f(x) определена и не имеет точек разрыва на данном отрезке [a, b], и требуется найти все корни уравнения
f (x) 0
на заданном отрезке [a, b], то это можно сделать путем непосредствен ного последовательного вычисления функции в точках x1 a, x2, x3,…, xn b с шагом -x на всем отрезке [a, b] и выделении в качестве корней точек xk , при переходе которых функция меняет знак. Для об наружения этих точек достаточно проверять знак произведения двух последовательных значений функции f (xk 1) f (xk), которое меньше нуля, если корень между этими точками, или равно нулю, если корень совпадает с одной из этих точек.
Например, если требуется вычислить корни с точностью до чет вертого знака после запятой, то нужно задать -x 0,0001. Ниже при веден текст Фортран программы, где в качестве примера задано урав нение
x exp( x) 0.
Значения функции f(x) вычисляются в цикле с параметром цикла х и шагом dx -x 0,0001. ПриM62всех вычислениях на каждом этапе цик ла имеются только два значения функции: предыдущее Yp f (x) и по лучаемое Y f (x dx). Причем первое значение функции f(x) при x a вычисляется перед циклом и ему присваивается имя Yp. Затем в цикле каждому вновь вычисленному Y(x) после выяснения знака про изведения Y Yp присваивается имя Yp.
PROGRAM Korni
OPEN(11,FILE=’KORNI.txt’)
a=0.; b=20.; dx=0.0001; x=a; Yp=f(x)
a=a+dx; |
k=1 |
! k — номер найденного корня |
|
DO |
x=a, |
b, |
dx |
|
Y=f(x); |
Znak=Y*Yp |
|
IF(Znak) |
Then |
||
! Запись корня на экран |
|||
WRITE(*,’(2x,A,I4,3x,A,F8.4)’)’k=’, k, ‘x=’,x |
|||
! Запись |
корня в |
файл |
|
WRITE(11,’(2x,A,I4,3x,A,F8.4)’) ‘k=’, k, ‘x=’, x CALL SLEEPqq(500) ! Пауза 0.5 секунды
k=k+1
EndIF
Yp=Y
ENDDO

|
2.19. Интерполирование |
139 |
|
К=к 1 |
|
|
|
WRITE(*,’(2x,A,I4)’) ‘NUMBER of the found roots |
k=’,k |
||
END |
PROGRAM |
Korni |
|
FUNCTION f(x) |
|
|
|
f=х Exp( x) |
|
|
|
END |
FUNCTION |
F |
|
Рассмотренный способ иллюстрирует возможность вычислить ко рень с помощью компьютера с любой заданной точностью. В данном примере корень только один: x 0,5672.
Представленные выше методы тоже полезно знать. Если, напри мер, при решении данного уравнения использовать метод касатель ных, то уже в первом приближении мы получим x1 0,5. В данном слу чае при x a и функция, и ее вторая производная одного знака:
f (0) 1, |
f (0) 1. |
Поэтому нужно записать уравнение касательной на левой границе
данного отрезка. Тогда получим
Для вычисления второго приближения потребуется калькулятор:
f (0) f (0)(x1M620) 0 1 x1 0 x1 0,5.
f (x ) f (x )(x |
x ) 0 |
x |
0,5 |
0,5 |
e 0,5 |
0,5663. |
|||
|
|
|
|||||||
|
|
||||||||
1 |
1 |
2 |
1 |
2 |
|
|
1 e 0,5 |
|
|
|
|
|
|
|
|
|
|
||
Как видим, при использовании метода касательных (Ньютона) не обходимо четко знать, на каком конце отрезка нужно проводить каса тельную. Тогда процесс вычислений сходится, и очень быстро.
2.19. Интерполирование
Постановки задачи. Интерполяционный многочлен Лагранжа. Интерпо ляционный многочлен Ньютона. Численное дифференцирование.
2.19.1. Постановки задачи
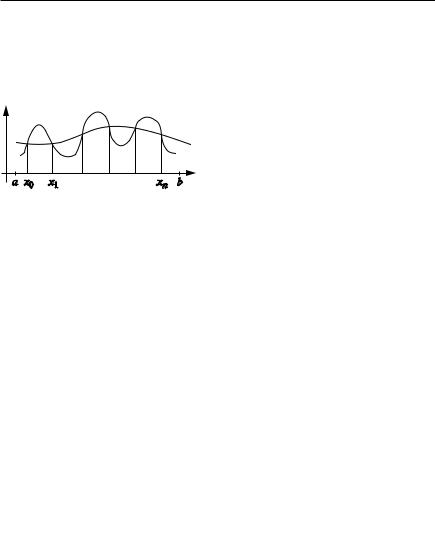
Пусть известно, что между переменными x и y существует функцио нальная зависимость y f (x), и на основании эксперимента установле ны значения этой функции y0, y1, , yn при некоторых значениях аргу мента x0, x1, …, xn, принадлежащих отрезку [a, b]. Т. е. y0 f (x0), y1 f (x1), …, yn f (xn). Требуется найти многочлен Pn(x) степени не
140 Глава 2. Дифференциальное исчисление функций одной переменной
выше n, значения которого в точках x0, x1, …, xn совпадают со значения ми функции f (x) в этих точках:
Pn(x0) y0, Pn(x1) y1, |
, |
Pn(xn) yn. |
(1) |
||
Точки x0, x1, …, xn — узлы интерполяции. |
|
|
|||
|
Такую |
задачу |
называют задачей |
||
|
интерполирования, |
а |
многочлен |
||
|
Pn(x) — интерполяционным многочле |
||||
|
ном. Если Pn(x) найден, |
то считая |
|||
|
Pn(x) = f (x) на [a, b], мы можем нахо |
||||
|
дить приближенно значения функции |
||||
Рис. 2.42 |
f (x) в точках x, лежащих между точка |
||||
ми x0 |
, x1, …, xn. |
|
|
||
|
|
|
|||
Покажем, что задача интерполирования имеет единственное реше ние. Действительно, пусть многочлен Pn(x) найден и имеет вид
|
P (x) a xn |
a xn 1 |
a . |
|
n |
M62n 1 |
|||
|
n |
0 |
1 |
n |
Из условий (1) вытекает, что коэффициенты ai (i 0, …, n) удовлетво ряют следующей системе уравнений:
a x |
|
a x |
|
a |
|
x |
a |
n |
y |
, |
||
& |
0 0 |
1 0 |
|
n 1 |
0 |
|
|
0 |
|
|||
& |
|
n |
a x |
n 1 |
a |
|
x |
a |
|
|
y , |
|
&a x |
|
|
|
n |
(2) |
|||||||
|
0 1 |
1 1 |
|
n 1 |
1 |
|
1 |
|||||
&. . . . . . . . . . . . . . . . . . . . . . . |
|
|||||||||||
& |
|
|
a xn 1 |
a |
|
x a |
|
y . |
||||
&a xn |
n 1 |
n |
||||||||||
|
0 n |
1 n |
|
n |
|
|
n |
|
||||
Система (2) — система n 1 уравнений с n 1 неизвестной. Опреде литель
xn |
xn 1 |
x |
1 |
0 |
0 |
0 |
|
xn |
xn 1 |
x |
1 |
1 |
1 |
1 |
|
|
|
||
xn |
xn 1 |
x |
1 |
n |
n |
n |
|
носит название определителя Вандермонда. Он всегда отличен от 0 при различных x0, x1, …, xn. Таким образом, система (2) имеет единст венное решение и, следовательно, многочлен Pn(x) — единственный.
Существуют различные способы построения многочлена.
