Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Санкт-Петербургский государственный архитектурно-строительный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Основы высшей математики для инженеров 2009

.pdf
Скачиваний:
225
Добавлен:
12.03.2016
Размер:
10.04 Mб
Скачать
☆

5.2. Интеграл Пуассона. Гамма2функция

241

Возьмем производную от обеих частей равенства (3). Производная от левой части равенства вычисляется по правилу дифференцирования функции с переменным верхним пределом, при этом получаем

7L

b

:

b

9Dd)D f (x, ))dx<

D f (x, L)dx.

9

a

<

 

a

8c

;L

L

Положим ((x, L) D f (x, ))d)C Тогда интеграл в правой части равенст

c

ва (3) примет вид

b

D((x, L)dx.

a

Производную последнего интеграла вычислим по теореме Лейбница.

7b

99D((x, L)

8a

Производные от левой и тельно,

L b

:

b

b

dx< D(L(x, L)dx D f (x, L)dx.

<

a

a

;L

M62

правой части равенства (3) совпали, следова

 

b

L

Dd)D f (x, ))dx DdxD f (x, ))d) C.

(4)

c a

a c

 

Полагая в (4) L C, получим, что C 0. Положив в равенстве (3) L d, убеждаемся в справедливости равенства (2).

Теорема доказана.

5.2. Интеграл Пуассона. ГаммаNфункция

Интеграл Пуассона. Гамма функция и ее свойства.

5.2.1. Интеграл Пуассона

Интегралом Пуассона называется несобственный интеграл De x2 dx.

0

Этот интеграл имеет многочисленные приложения в различных разде лах математики, механики, физики. К необходимости его вычисления

242 Глава 5. Интегральное исчисление функций многих переменных

приводит, например решение уравнения теплопроводности. Он возни кает также при решении задач математической статистики.

Значение интеграла Пуассона не может быть найдено с использо ванием формулы Ньютона – Лейбница, поскольку первообразная от

функции e x2 не выражается через элементарные функции. Мы вос пользуемся здесь для вычисления этого интеграла свойствами инте гралов, зависящих от параметра.

Положим x t, где 0. Тогда dx dt;

 

 

 

J De x

2 dx De 2t

2 dt.

00

Умножим обе части последнего равенства на e 2 d :

 

 

 

J e 2 d e 2 d De 2t

2 dt.

(1)

0

 

 

Проинтегрируем обе части равенства (1) по в пределах от 0 до .

Будем иметь

 

M62

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J De 2 d J

De 2

d De 2t

2 dt.

(2)

 

0

 

0

0

 

 

Согласно доказанной ранее теореме, в равенстве (2) изменим порядок интегрирования и получим

 

 

t

2

)

2

 

7

1

 

 

 

 

t

2

)

2 :

1

 

dt

 

J2 Ddt De

(1

 

 

d D9

 

 

 

 

 

 

e

(1

 

< dt

 

D

 

 

 

 

 

 

 

 

(1 t2)

 

 

 

 

 

2

1 t2

0

0

 

 

 

 

 

0

8 2

 

 

 

 

 

 

 

;

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

arctg t|0

'

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

Таким образом, окончательно имеем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

J

 

'

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.2.2. Гамма>функция и ее свойства

Гамма функцией (или интегралом Эйлера второго рода) называет ся интеграл вида

 

 

M(p) De x xp 1dx.

(3)

0

5.2. Интеграл Пуассона. Гамма2функция

243

Интеграл (3) — функция параметра p — является несобственным, так как верхний предел равен бесконечности и, кроме того, потому что при x 0 и p 1 подынтегральная функция неограниченно возрастает.

Покажем, что этот несобственный интеграл существует (сходится) при p 0. Представим его в виде суммы

 

1

 

D xp 1e xdx D xp 1e xdx D xp 1e xdx.

0

0

1

Первый интеграл правой части сходится, так как

1

1

1

 

0 D xp 1e xdx D xp 1dx

.

 

0

0

p

 

 

Второй интеграл также сходится. Действительно, пусть n — целое число такое, что n p 1. Тогда, очевидно,

0 D xp 1e xdx D xne xdx.

M1 612

Последний интеграл сходится и вычисляется путем интегрирования по частям с учетом того, что

xk

lim

0

(4)

x ex

 

 

при любом целом положительном k. Итак, интеграл (3) определяет не которую функцию. Эта функция часто используется в приложениях математики.

Найдем значения M(p) при целых p. При p 1 имеем

 

 

M(1) De xdx 1.

(5)

0

 

Пусть целое p 1. Вычислим M(p 1) путем интегрирования по час тям:

 

 

 

 

 

 

 

xp u,

pxp 1dx du,

 

M(p 1) D xpe xdx

 

 

0

 

 

 

 

 

 

e xdx dv,

v e x

 

 

 

 

 

 

 

 

 

 

(6)

 

 

 

 

 

 

 

 

 

 

 

x

 

p 1

 

 

 

 

p 1 x

 

 

e

px

 

pD x

dx pM(p).

 

 

 

 

0

e

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 
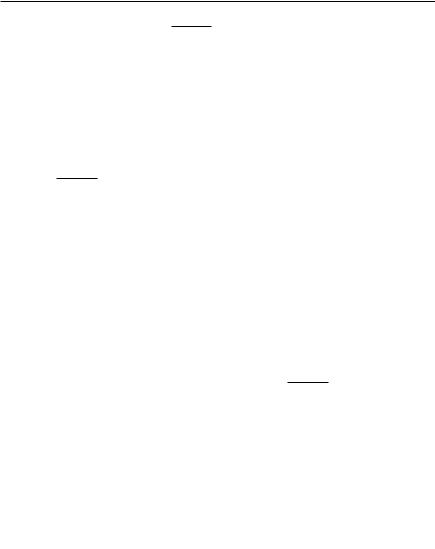
тельных значений аргумента p. Так как M(p)

244 Глава 5. Интегральное исчисление функций многих переменных

Из этого следует M(p) M(p 1). p

На основании (6) и (5) находим при p n

M(n) (n 1)!

(7)

Полагая в формуле (7) n 1, находим, что 0! M(1) 1. Функция M(p) дает возможность распространить понятие факториала n!, определен ного лишь для натуральных значений n, на область любых положи тельных значений аргумента. Из формулы (6) следует, что если p 0,

то M(p) M(p 1) , т. е. M(0) . p

После n кратного применения формулы (6) получаем соотно

шение

 

 

 

 

 

 

 

 

 

 

(8)

 

M(p n) (p n 1)(p n 2) (p 1)M(p).

 

 

При p n 1 из формулы (6) следует, что

 

 

 

 

 

 

т. е. M( n) ( 1)n

 

(n 1,M2, 3, …)62.

 

 

n M(0)

 

 

 

M( n)

M( n 1)

M( n 2)

( n 3)

 

( 1)

( 1)

n

,

 

 

 

 

 

 

 

 

 

n

 

n(n 1)

n(n 1)(n )

 

 

 

n!

 

 

 

Вообще, функцию M(p) можно распространить на случай отрица

M(p 1), то M(p 1) имеет p

смысл при 1 p 0.

Если n p (n 1), то из формулы (8) следует, что

M(p)

M(p n)

.

 

p(p 1)(p 2) (p n 1)

С помощью подстановки p n ), откуда p n ), последняя фор мула преобразуется к виду

M() n)

( 1)n M())

,

(1 ))(2 )) (n ))

 

 

и для n p (n 1) знак M(p) определяется множителем ( 1)n. Можно показать, что перечисленные свойства функции M(p) позволяют вычис лить ее значения для любого p. Значения M(p) функции табулированы. Эта таблица находит самые разнообразные приложения.

5.3. Двойной интеграл

245

5.3. Двойной интеграл

Задача об объеме, приводящая к понятию двойного интеграла. Опреде ление двойного интеграла. Теорема существования. Свойства двойного интеграла. Вычисление двойного интеграла в декартовых координатах.

Понятие кратного интеграла является естественным обобщением понятия обыкновенного определенного интеграла на случай функции нескольких переменных. Эти понятия возникли и развивались парал лельно и находят широкие сферы применения.

Кратные интегралы применяются в геометрии (вычисление пло щадей плоских фигур и поверхностей, объемов тел), механике (вычисление статистических моментов, координат центра тяжести, моментов инерции тел), физике и многих других разделах науки.

С понятием кратного интеграла, его свойствами, способами вы числения и сферами применения мы и познакомимся в этом разделе.

5.3.1. Задача об объеме,M62приводящая к понятию двойного интеграла

Пусть N — некоторая область в плоскости XOY, ограниченная замкнутым контуром l. Рассмотрим тело, ограниченное областью N, цилиндрической поверхностью с направляющей l и образующей, па раллельной оси OZ, и частью поверхности S, имеющей уравнение z f (x, y), где f — функция, определенная, непрерывная и неотрица тельная в N.

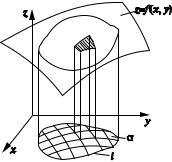
Поставим задачу определить объем полученного тела. Для этого поступим следующим образом: разобьем N на малые площадки -Ni

n

(i 1, 2, …, n), F-Ni N. На каждой пло

i 1

щадке построим цилиндр, ограниченный

 

сверху частью поверхности S, проектирую

 

щейся в -Ni. Полученные n цилиндриче

 

ских столбиков имеют объемы -Vi, при

 

n

 

чем F-Vi V .

 

i 1

 

Рассмотрим теперь цилиндр с основа

 

нием -Ni и с высотой zi f (xi, yi),

 

(xi, yi) -Ni. Объем такого цилиндра,

Рис. 5.1

равный произведению площади основа

 

246 Глава 5. Интегральное исчисление функций многих переменных

ния -Ni на высоту f (xi, yi), примем за приближенное значение объ ема столбика

-Vi = f (xi, yi)-Ni.

Тогда сумма Vn этих элементарных объемов будет приближенным вы ражением искомого объема:

nn

Vn F-Vi = F f (xi, yi)-Ni.

i 1 i 1

За V примем предел, к которому стремится выписанная сумма, при условии, что число площадок -Ni неограниченно увеличивается, а сами площадки стягиваются в точку:

 

n

 

V lim

F f (xi, yi)-Ni.

 

n

 

 

diam -Ni 0 i 1

(1)

Итак, задача о вычислении объема привела к необходимости вы числения предела интегральнойM62суммы (1).

5.3.2. Определение двойного интеграла. Теорема существования

Если максимальный размер элементарных площадок -N1 стремит ся к нулю, а n , и существует предел интегральной суммы (1), ко торый не зависит ни от способа разбиения области N, ни от выбора то чек (xi, yi), то он называется двойным интегралом от функции f (P) f (x, y) по области N:

 

 

 

n

DD f (x, y)dN

lim

 

F f (xi, yi)-Ni.

N

n

 

i 1

( )

diam -Ni

0

 

 

 

Здесь N — область интегрирования, f (x, y) — подынтегральная функ ция, dN — элемент площади.

Возвращаясь к задаче об объеме, видим, что объем цилиндриче ского тела численно равен двойному интегралу от аппликаты z f (x, y) по области N:

V DD f (x, y)dN.

(N)

В этом состоит геометрический смысл двойного интеграла.

5.3. Двойной интеграл

247

З а м е ч а н и е. Если f(x, y) J1, то DDdN N, где N — площадь области.

(N)

nn

F f(xi, yi) -N i F-N i N,

i 1

i 1

 

т. е.

f

 

 

 

lim

F-N i N DDdN.

n

0 i 1

(N)

diam -N i

Теорема существования.

Для всякой

функции f (x, y), непрерывной

в ограниченной и замкнутой области N, существует двойной интеграл по этой области, т. е. существует предел интегральной суммы, не завися2 щий ни от способа разбиения области N, ни от выбора точек Pi(xi, yi).

Из теоремы существования следует, что область N можно разбивать на прямоугольники -Ni -xi -yi со сторонами -xi и -yi прямыми, па раллельными осям координат.

В связи с этим часто пишут, что

 

 

 

n

 

DD f (x, y)dxdy

lim

 

F f (xi, yi)-xi -yi.

 

N

n

 

i 1

 

( )

diam -Ni

0

 

 

 

 

 

Погрешностью, которая

M62возникает здесь при

 

замене прямоугольных кусков на границе об

Рис. 5.2

ласти на прямоугольники, можно пренебречь.

5.3.3. Свойства двойного интеграл

Легко заметить, что конструктивно двойной интеграл определяет ся точно так же, как и определенный интеграл. Поэтому его свойства вполне аналогичны свойствам определенного интеграла.

1. DDkf (x, y)dN k DD f (x, y)dNC

(N)

(N)

2. DD f1(x, y)dN DD f2(x, y)dN DD[f1(x, y) f2(x, y)]dN.

(N)

(N)

(N)

3.Если f (x, y) 0 в области N, то

DDf (x, y)dN 0.

(N)

248Глава 5. Интегральное исчисление функций многих переменных

4.Если f (x, y) ((x, y) в области N, то

DD f (x, y)dN DD((x, y)dN.

(N) (N)

5. Теорема о среднем. Если f (x, y) непрерывна в замкнутой ограничен2 ной области N, то P0(x0, y0) N такая, что

DD f (x, y)dN f (x0, y0) N.

(N)

Геометрический смысл: если f (x, y) 0, то объем цилиндрического тела равен объему цилиндра с тем же основанием и высотой, равной значению подынтегральной функции в некоторой точке P0(x0, y0) N.

6. Свойство аддитивности. Если область N разбита на несколько частей N1, N2 , …, Nk , то

DD f (x, y)dN DD f (x, y)dN DD f (x, y)dN

DD f (x, y)dN.

 

(N1)

M62

(Nk )

(N)

(N )

5.3.4. Вычисление двойного интеграла в декартовых координатах

Пусть для простоты f (x, y) 0, а область интегрирования ограниче на двумя вертикальными прямыми и графиками функций y (1(x), y (2(x), (2(x) (1(x).

С одной стороны, объем тела, ограниченного поверхностью z f (x, y), равен двойному интегралу:

V DD f (x, y)dN,

(N)

но, с другой, его можно вычислить и с по мощью определенного интеграла по коорди нате х, если определить площади S(x) сече ний данного тела плоскостями, перпендику лярными оси x (см. 3.11.1):

 

b

 

 

V DS (x)dx,

(2)

Рис. 5.3

a

 

где S (x) — площадь сечения тела плоскостью, перпендикулярной оси OX (рис. 5.4).

5.3. Двойной интеграл

249

Но

yвых

S (x) D f (x, y)dy.

yвх

Здесь x фиксировано.

Подставим теперь S(x) в определенный ин теграл (2):

 

b (2(x)

#

b

(2(x)

 

&

 

&

 

 

V

D

D f (x, y)dy$dx Ddx D f (x, y)dy. (3)

 

&

 

&

a

(1(x)

 

a (1(x)

%

Рис. 5.4

Итак, для вычисления двойного интеграла нужно сначала вычислить обычный интеграл:

(2(x)

S (x) D f (x, y)dy,

(1(x)

считая x постоянным. ЭтотM62интеграл будет функцией от x. Затем

нужно вычислить

b

DS (x)dx,

a

где a, b — пределы изменения x.

Если область интегрирования имеет вид, изображенный на рис. 5.5, где (2(y) (1(y), то

b(2( y)

DD f (x, y)dN Ddy

D f (x, y)dx.

(4)

(N)

a

(1(x)

 

Интегралы в правых частях формул (3) и (4) называются повторными или двукратными.

Если область интегрирования более слож ная, то ее разбивают на более простые и поль зуются свойством аддитивности.

Если область интегрирования — прямо угольник, ограниченный прямыми x a, x b, y c, y d, то

Рис. 5.5

b d d b

DD f (x, y)dN DdxD f (x, y)dy DdyD f (x, y)dx.

(N)

a c

c a

250 Глава 5. Интегральное исчисление функций многих переменных

 

 

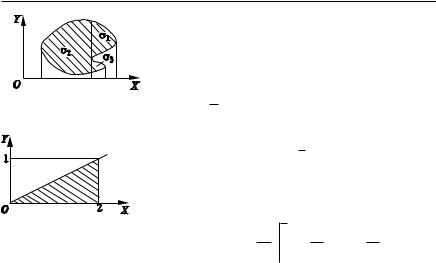
П р и м е р.

Вычислить

 

DD(x2 y2)dN,

 

 

 

 

 

 

 

 

 

 

 

 

(N)

 

 

где

область

N

ограничена

 

прямыми y 0,

Рис. 5.6

x

2, y

x

.

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

DD(x2 y2)dN DdxD(x2 y2)dy

 

 

(N)

 

 

 

 

0

0

 

 

 

 

 

 

 

2

 

 

x

2

 

 

 

 

 

Рис. 5.7

 

2

y3 2

13

 

3

13

.

 

 

Ddx x y

D

24

x dx

 

 

0

 

 

3

0

0

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

5.4. Замена переменныхM62в двойном интеграле

Замена переменных в двойном интеграле. Двойной интеграл в поляр ных координатах.

5.4.1. Замена переменных в двойном интеграле

Пусть в плоскости XOY задана область D, ограниченная линией l. Пусть координаты x, y являются функциями новых переменных u и v:

x ((u, v),

y >(u, v),

(1)

причем функции ((u, v), >(u, v) однозначны, непрерывны и имеют не прерывные производные в некоторой области D . Тогда по форму лам (1) каждой паре значений u, v ставится в соответствие пара значе ний x, y. Предположим далее, что по каждой паре значений x, y из D мы можем по уравнениям (1) найти значения u, v. Тогда по области D мы можем построить область D , лежащую в плоскости UOV и ограни ченную линией l . Здесь каждой точке области D соответствует некото рая определенная точка области D и обратно, каждой точке из D со ответствует точка из D. Говорят, что между областями D и D установ лено взаимно однозначное соответствие.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности