|
3.7. Определенный интеграл: постановка задачи… |
171 |
b |
b |
b |
|
2. D[f (x) / ((x)]dx D f (x)dx / D((x)dx. |
|
a |
a |
a |
|
Доказательство аналогично.
3. Если отрезок [a, b] разбит на две части [a, c] и [c, b], то
D f (x)dx D f (x)dx D f (x)dx.
Доказательство. Так как предел интегральной суммы не зависит от способа разбиения отрезка [a, b], то при составлении интегральной суммы включим точку с в точки разбиения: c xk . Тогда
n |
|
|
k |
|
|
n |
|
|
|
|
F f (Ai)-xi F f (Ai)-xi F f (Ai)-xi; |
i 1 |
|
|
i 1 |
|
|
i k 1 |
|
|
b |
i |
|
|
n |
|
|
|
i |
|
b |
k |
|
|
M62n A - c |
|
F f (Ai)-xi |
D f (x)dx |
lim |
|
|
F f (Ai)-xi |
lim |
|
|
a |
n |
|
i 1 |
|
|
n |
|
i 1 |
|
max -x |
0 |
|
|
|
max -x |
0 |
|
|
lim |
|
F f ( |
i) xi |
D f (x)dx |
|
D f (x)dx. |
|
n |
|
i k 1 |
|
a |
|
|
c |
|
max -xi 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
З а м е ч а н и е. Свойство 3 |
было |
сформулировано для случая, когда |
a c b. Однако оно остается справедливым и для случая, когда c [a, b]. Пусть, например, c a b. Тогда
|
b |
a |
b |
|
D f(x)dx D f(x)dx D f(x)dx. |
|
c |
c |
a |
a |
c |
|
|
Но D f(x)dx D f(x)dx. Поэтому
ca
b c b b c b
D f(x)dx D f(x)dx D f(x)dx D fdx D fdx D fdx. c a a a a c
b
4. Если f (x) 0 на [a, b], то D f (x)dx 0 на [a, b].
172 |
Глава 3. Интегральное исчисление функций одной переменной |
|
|
|
|
n |
|
Доказательство. f (Ai) 0, |
-xi 0 F f (Ai)-xi 0 |
|
|
|
|
i 1 |
|
|
|
n |
|
|
lim |
|
F f (Ai)-xi 0. |
|
n |
|
|
|
max -xi 0 i 1 |
|
|
|
|
b |
b |
|
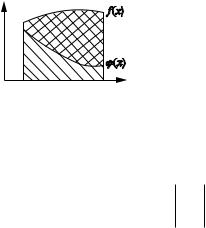
5. f (x) 0, ((x) 0, f (x) ((x) D f (x)dx D((x)dx. |
|
|
|
a |
a |
|
|
|
b |
|
Доказательство. f (x) ((x) 0 D(f (x) ((x))dx 0
ab b
D f (x)dx D((x)dx.
aa
На рис. 3.3 дана геометрическая интерпрета
ция данного свойства — одна трапеция содержит |
f (x)| f (x) M62| f (x)| D| f | dx D fdx D| f | dx, |
другую. |
|
|
b |
b |
b |
a |
a |
a |
bb
D fdx D| f | dx.
aa
6.Если m и М — наименьшее и наибольшее значения функции на [a, b], то
b
m(b a) D f (x) dx M(b a).
a
Доказательство. Так как m f (x) M, то
Dm dx D f (x) dx DM dx
и
b
m(b a) D f (x) dx M(b a).
3.8. Определенный интеграл: теорема о среднем… |
173 |
3.8. Определенный интеграл: теорема о среднем, формула Ньютона Лейбница, замена переменной, интегрирование по частям
Теорема о среднем значении определенного интеграла. Вычисление определенного интеграла. Формула Ньютона – Лейбница. Замена пе ременных в определенном интеграле. Интегрирование по частям в оп ределенном интеграле.
3.8.1. Теорема о среднем значении определенного интеграла
Если f (x) непрерывна на [a, b], то на [a, b] найдется такая точ ка с, что
b |
|
D f (x)dx f (c)(b a). |
(1) |
a |
|
Доказательство. Так как f (x) непрерывна на [a, b], то она ограни |
m(b M62a) f (x)dx (b a) |
|
чена, поэтому m f (x) M, следовательно, выполнено неравенство |
b |
|
D |
|
a |
|
(свойство 6 определенного интеграла). Обозначим 1 |
b |
D f (x)dx . |
b a a
Тогда из последнего неравенства вытекает, что m M.
По свойству непрерывных функций существует такое с: a c b, что f (c) и называется средним значением функции на отрезке [a, b]:
|
|
1 |
b |
b |
|
f (c) |
D f (x)dx D f (x)dx f (c)(b a). |
|
b a |
|
|
a |
a |
|
|
|
|
Геометрическая |
интерпретация. Площадь |
криволинейной трапеции равна площади пря моугольника с тем же основанием и высотой, равной ординате кривой в некоторой проме жуточной точке с (рис. 3.4).
174Глава 3. Интегральное исчисление функций одной переменной
3.8.2.Вычисление определенного интеграла. Формула Ньютона – Лейбница
b
Пусть в определенном интеграле D f (x)dx, где f (x) — непрерывная
a
функция, нижний предел закреплен, верхний предел меняется. Тогда будет меняться и значение определенного интеграла, т. е. он будет функцией переменного верхнего предела.
Обозначим переменный верхний предел через x, а переменную ин тегрирования через t. Тогда
x
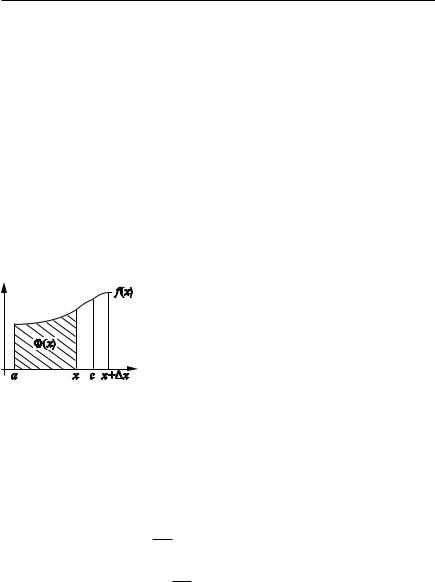
E(x) D f (t)dt.
a
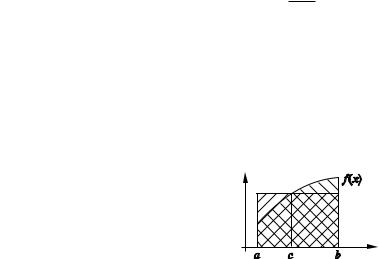
Если f (x) 0, то E(x) — переменная площадь криволинейной трапе ции. Она меняется при изменении x (рис. 3.5).
|
Найдем производную E(x) по x. Для этого |
|
M62E(x -x) D f (t)dt E(x) D f (t)dt, |
дадим x приращение -x: |
|
|
x -x |
x -x |
|
a |
x |
|
|
x -x |
Рис. 3.5 |
-E E(x -x) E(x) |
D f (t)dt. |
|
|
x |
|
x -x |
|
Применим к интегралу |
D f (t)dt теорему о среднем значении: |
|
x |
|
|
x -x |
|
|
D f (t)dt f (c)-x, |
|
|
x |
|
где x c x -x. Тогда |
-E f (c). При -x 0 c x; |
|
-x |
|
lim -E lim f (c) f (x)
-x 0 -x -x 0
(в силу непрерывности функции f (x)). Окончательно,
E(x) f (x).
3.8. Определенный интеграл: теорема о среднем… |
175 |
Таким образом, производная определенного интеграла по переменно му верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
З а м е ч а н и е. Мы попутно доказали, что всякая непрерывная функ ция имеет первообразную. Действительно, из равенства (2) следует, что E(x) есть первообразная для f(x).
Теорема. Если F(x) есть какая2либо первообразная от непрерывной функции f (x), то
b |
|
D f (x)dx F(b) F(a). |
(3) |
a |
|
Доказательство. Пусть F(x) — какая либо первообразная для f (x).
x
Так как E(x) D f (x)dx также первообразная, а все первообразные от
a
личаются на постоянную,M62то
x
D f (t)dt F(x) C.
a
Найдем С. При x a имеем
a
D f (t)dt 0 F(a) C;
a
поэтому C F(a),
x
D f (t)dt F(x) F(a).
a
При x b получаем формулу (3). Иногда ее записывают в виде
b
D f (x)dx F(x)|ba F(b) F(a).
a
Таким образом, определенный интеграл равен приращению первооб разной на отрезке интегрирования.
176 |
Глава 3. Интегральное исчисление функций одной переменной |
Формула (3) была получена И. Ньютоном и Г. Лейбницем. С ее от крытием математика получила практический удобный метод вычисле ния интеграла, и только тогда интеграл получил то значение в решении прикладных задач, которое он имеет сейчас. Пределы же интегральных сумм считал еще Архимед, а Иоганн Кеплер в свое время опубликовал книгу «Новая стереометрия винных бочек» в которой привел результа ты вычисления объемов тел вращения с помощью интегральных сумм.
З а м е ч а н и е. Для разрывных подынтегральных функций формула Ньютона – Лейбница может не иметь места.
3.8.3. Замена переменной в определенном интеграле
Для вычисления определенного интеграла, так же, как и для вы числения неопределенного интеграла, удобно прибегать к замене пе ременной.
Теорема. Пусть дан интегралM62
b
D f (x)dx,
a
где f (x) непрерывна на [a, b].
Введем новую переменную по формуле x ((t). Пусть числа ) и * таковы, что:
1)(()) a, ((*) b;
2)((t) и ( (t) непрерывны на [), *];
3)f [((t)] определена и непрерывна на [), *].
Тогда
b*
D f (x)dx D f [((t)]( (t)dt.
a)
Доказательство. Если F(x) — какая либо первообразная для f (x), то
b |
|
D f (x)dx F(b) F(a). |
(4) |
a
По формуле, которая была выведена для неопределенного интеграла,
D f [((t)]( (t)dt F[((t)] C.
3.8. Определенный интеграл: теорема о среднем… |
177 |
Поэтому
* |
|
D f [((t)]((t)dt F[((t)]|*) F[(())] F[((*)] F(b) F(a). |
(5) |
) |
|
Так как правые части в (4) и (5) совпадают, то равны и их левые
части, поэтому
b *
D f (x)dx D f [((t)]((t)dt.
a)
П р и м е р 1.
|
|
|
x sin t; dx cost dt, |
' |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
D 1 x2 dx |
0 sin ) ) 0, |
Dcos2t dt. |
0 |
|
|
1 sin * * |
' |
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
П р и м е р 2.
D |
|
|
M62dx |
D |
2 |
|
|
|
ln 2 |
|
|
еx 1 t |
, |
x ln (t2 1) |
1 |
2t |
2 |
dt |
|
еx 1 dx |
|
|
) 0, |
|
|
t dt |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 t 1 |
0 |
|
|
* 1, |
|
|
t2 1 |
|
3.8.4. Интегрирование по частям в определенном интеграле
Пусть u(x) и v(x) — дифференцируемые на [a, b] функции. d(uv) udv vdu,
b b b
Dd(uv) Dudv Dvdu.
a a a
Но Dd(uv) (uv)|ba Dudv uv |ba Dvdu.
a |
a |
|
|
a |
|
|
|
|
|
П р и м е р. |
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
' |
|
' |
|
|
|
2 |
|
2 |
|
' |
|
|
D x cos x dx x sin x|2 |
Dsin x dx x sin x|2 cos x|2 |
|
1. |
|
|
0 |
|
0 |
|
0 |
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
178 |
Глава 3. Интегральное исчисление функций одной переменной |
3.9. Геометрические приложения определенного интеграла
Вычисление площадей плоских фигур в прямоугольных координатах. Вычисление площадей для случая задания их границ уравнениями в параметрической форме. Вычисление площади криволинейного секто ра в полярных координатах.
3.9.1. Вычисление площадей плоских фигур в прямоугольных координатах
1. Пусть f (x) 0 — непрерывная на [a, b] функ
ция. Тогда
b
S D f (x)dx.
a
2. Если f (x) 0 на [a, b], то из соображений
симметрии
b
S D f (x)dx.
M62a
3. Если f (x) меняет знак на [a, b], то разбиваем отрезок [a, b] на сумму отрезков, на каждом из кото рых знак функции f (x) постоянен.
|
D f dx D f dx D f dx D f dx. |
|
a |
a |
c |
d |
|
b |
|
|
|
|
Тогда D f dx дает разность площадей, лежа |
Рис. 3.8 |
a |
|
|
|
щих ниже выше оси OX. Чтобы получить пло щадь в обычном смысле, нужно на тех отрезках, где f (x) 0, заменить ее на f (x), т. е.
c |
d |
b |
b |
S D f dx D f dx D f dx D| f | dx. |
a |
c |
d |
a |
4. Если нужно вычислить |
площадь, |
ограниченную кривыми |
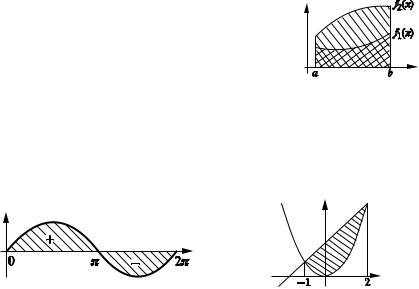
y f1(x), y f2(x) (f2(x) f1(x)) на [a, b], то вычисляют ее как разность площадей криволинейных трапеций (рис. 3.9):
bb
S D f2(x)dx D f1(x)dx.
3.9. Геометрические приложения определенного интеграла |
179 |
Мы рассмотрели случай, когда f2(x) f1(x) 0. Однако для любых f1(x) и f2(x) таких, что f2(x) f1(x), имеет место формула
b
S D[ f2(x) f1(x)]dx.
a
П р и м е р ы. Вычислить площадь, ограниченную синусоидой y sin x и осью OX при x [0, 2'].
'2'
S Dsin xdx Dsin xdx 4 (ед2).
0'
Рис. 3.10 |
|
Рис. 3.11 |
|
|
Вычислить площадь, ограниченную параболой |
2 |
|
|
|
y x 2. |
M62 |
|
y |
|
x |
и прямой |
Здесь удобнее рассматривать x как функцию от y, т. е. поменять местами обозначения аргумента и функции. Тогда y x2 , x y 2
y x 2,
2
S D(x 2 x2)dx.
1
3.9.2.Вычисление площадей для случая задания их границ уравнениями
впараметрической форме
Пусть криволинейная трапеция ограничена кривой, заданной уравнениями в параметрической форме: x ((t), y >(t), где t [), *]. Пусть на отрезке [a, b] эти уравнения определяют некоторую кривую y f (x) ((()) a, ((*) b).
bb
S D f (x)dx D ydx.
dx ( (t)dt,
180 |
Глава 3. Интегральное исчисление функций одной переменной |
В последнем интеграле сделаем замену перемен ных x ((t). Тогда
y f (x) f [((t)] >(t),
и искомая формула примет вид
*
S D>(t)( (t)dt.
)
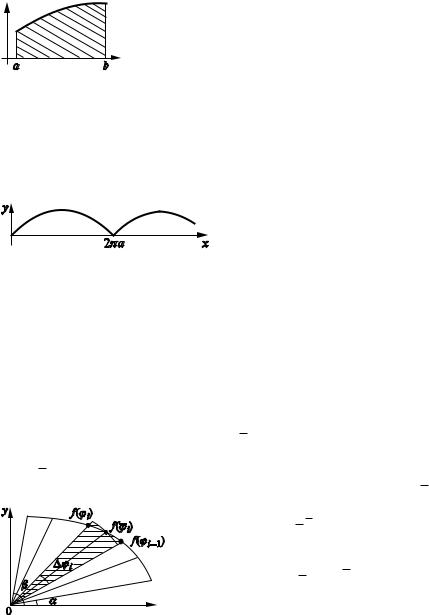
П р и м е р. Вычислить площадь, ограниченную одной аркой цик лоиды
x a(t sint), |
y a(1 cost). |
|
Циклоида — это траектория, описы |
|
ваемая точкой окружности радиу |
|
са a, которая катится без скольже |
|
ния по прямой — по оси OX. |
|
2'a |
2' |
Рис. 3.13 |
S D ydx Da2(1 cost)2 dt 3'a2. |
|
0 |
0 |
M62
3.9.3. Вычисление площади криволинейного сектора в полярных координатах
Пусть кривая в полярных координатах задана уравнением + f ((), |
где f (() — непрерывная функция на [), *]. Определим площадь сектора |
ОАВ. Для этого разобьем ОАВ на n частей радиусами векторами (0 ), |
(1, , (n *. Обозначим |
через -(i (i (i 1 |
углы |
между радиуса |
ми векторами. Обозначим через +i f ((i) радиус вектор, заключенный |
между |
f ((i) |
и |
f ((i 1) |
и |
соответствующий |
какому либо |
углу |
(i 1 (i (i. За площадь сектора, соответствующего углу -(i, примем |
приближенно площадь кругового сектора с тем же углом и радиусом +i: |
|
|
|
|
|
-S |
|
= 1 +2 -( . |
|
|
|
|
|
|
|
i |
|
2 |
i |
i |
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
n |
|
|
|
|
|
|
|
S F-Si = |
F f 2((i)-(i. |
|
|
|
|
|
|
i 1 |
|
|
2 i 1 |
|
|
|
Рис. 3.14 |
|
|
|
|
|
|
|
|
|