
Основы высшей математики для инженеров 2009
.pdf
1.10. Собственные векторы и собственные значения линейного оператора 51
x |
|
1 |
— одномерное линейное пространство собственных векто |
|
1 |
|
t |
|
|
x2 |
2 |
|
|
|
ров с базисом a2 (1, 2).
Отметим, что векторы a1, a2 в R2 образуют базис (векторы a1 и a2 неколлинеарны). Так как Aa1 a1, Aa2 13a2 , то матрица оператора А в этом базисе будет диагональной:
1 |
0 |
A |
. |
|
|
0 |
13 |
1.10.2. Условие диагональности линейного оператора
Теорема 1. Линейный оператор А в Rn приводится к диагональному виду тогда и только тогда, когда его собственные векторы образуют базис в Rn.
Доказательство. Необходимость |
( ). Пусть в базисе |
|
|
|
|
|
|
|||||
e1, e2 , …, en |
||||||||||||
матрица оператора А |
M62 |
|||||||||||
диагональная: |
|
|
|
|
|
|
|
|
|
|||
|
1 |
0 |
|
0 |
|
|||||||
|
|
0 |
|
|
0 |
|
||||||
|
A |
. |
||||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
0 |
|
|
|
||||||
|
|
|
n |
|||||||||
Тогда Ae1 1e1, Ae2 2 e2 , …, Aen nen, т. е. базис e1, …, en состоит из собственных векторов, отвечающих собственным значениям 1,
2, , n.
Достаточность. (.). Пусть e1, e2 , …, en — базис из собственных век торов, отвечающих собственным значениям 1, 2, , n.
Тогда Ae1 1e1, …, Aen nen и
|
0 |
|
0 |
|
|
|
|
|
|
A 0 |
|
|
0 |
. |
|
|
|||
0 0
Отметим, что не всякий линейный оператор приводится к диаго нальному виду, так как не всякий линейный оператор имеет хотя бы один собственный вектор. Примером такого оператора является опе ратор поворота в R2 на угол 0 ( '. Действительно, геометрически

52 Глава 1. Элементы линейной алгебры и аналитической геометрии
существование собственного вектора означает, что существует вектор, который растягивается оператором в раз, а оператор поворота все векторы не растягивает, а поворачивает.
Укажем достаточное условие приводимости оператора к диаго нальному виду.
Теорема 2. Если линейный оператор А в Rn имеет n различных собст2 венных значений, то собственные векторы, отвечающие им, образуют базис в Rn, и матрица оператора в этом базисе диагональная.
Доказательство для n 2. Пусть 1 2 — собственные значения, а e1, e2 — собственные векторы оператора А в R2 . Покажем, что эти векторы линейно независимы. Пусть
c1e1 c2 e2 0 0 A(c1e1 c2 e2) c1Ae1 c2 Ae2
и
c1Ae1 c2 Ae2 1c1e1 2 c2 e2 0.
Отсюда |
|
( 1 2)c2 e2 0, |
1 2. |
Значит, c2 0. Аналогично c1 0. Теорема доказана.
Теорема 3. Для любого самосопряженного оператора А в Rn сущест2 вует ортонормированный базис из собственных векторов, в котором его
M62
матрица является диагональной.
Доказательство в общем случае является очень сложным. Мы про ведем его для n 2, т. е. для оператора в R2, матрица которого в орто
нормированном базисе i , |
j имеет вид |
|
|
|||
A |
a |
a |
|
, |
a |
0 |
11 |
12 |
|
||||
|
a12 |
a22 |
|
|
12 |
|
|
|
|
|
|||
(иначе оператор уже диагональный).
1. оператор А имеет 2 различных собственных значения:
a11 a12 |
0 2 (a |
a |
) a a |
a2 |
0 |
||
a12 |
a22 |
11 |
12 |
11 |
22 |
12 |
|
|
|
|
|
|
|
||
дискриминант
D (a11 a22)2 4(a11a22 a122 ) (a11 a22)2 4a122 0,
следовательно, корни действительные и различные.
2. Собственные векторы, отвечающие различным собственным значениям, ортогональны:

1.11. Кривые и поверхности второго порядка |
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ae1 |
1e1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 2 ( 1 2)(e1, e2) 1(e1, e2) 2(e1, e2) Ae2 2 e2, |
||||||||||||||||||||||||||||||||
Ae2 |
2 e2, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
e1, e2) (e1, 2 e2) (Ae1, e2) (e1, Ae2) 0 |
||||||||||||||||||||||||||||||||
в силу теоремы 2 предыдущей лекции. Значит, (e1, e2) 0.
Из теоремы 2 и доказанных фактов вытекают все утверждения тео ремы 3 для n 2.
1.11. Кривые и поверхности второго порядка
Кривые второго порядка. Поверхности второго порядка.
Кривые второго порядка (эллипс, гипербола, парабола) как кони ческие сечения были известны уже математикам Древней Греции. С помощью этих кривых решались некоторые задачи на построение, оказавшиеся недоступными при использовании простейших чертеж ных инструментов — циркуля и линейки. Дальнейшие успехи теории кривых второго порядка связаны с созданием в XVII в. нового геомет рического метода — методаM62координат.
Интерес к этим кривым всегда поддерживался тем, что эти кривые часто встречаются в различных явлениях природы и в нашей деятель ности. В науке они приобрели особенное значение после того, как не мецкий астроном И. Кеплер открыл из наблюдений, а английский уче ный И. Ньютон теоретически обосновал законы движения планет, один из которых утверждает, что планеты и кометы Солнечной систе мы движутся по коническим сечениям, в одном из фокусов которых находится Солнце. Следующие примеры относятся к отдельным типам конических сечений: параболу описывает снаряд или камень, брошен ный наклонно к горизонту; в некоторых механизмах пользуются зубча тыми колесами эллиптической формы; гипербола служит графиком об ратной пропорциональности, часто наблюдающейся в природе (напри мер, закон Бойля – Мариотта). Очень многообразные применения в естествознании и технике имеют поверхности второго порядка.
1.11.1. Кривые |
второго порядка |
|
ОПРЕДЕЛЕНИЕ 1. Кривой |
второго порядка |
называется |
множество всех точек M(x, y) R2 , удовлетворяющих уравнению |
||
a11x2 2a12 xy a22 y2 b1x b2 y b0 0. |
(1) |
|
54 Глава 1. Элементы линейной алгебры и аналитической геометрии
Канонические уравнения кривых второго порядка
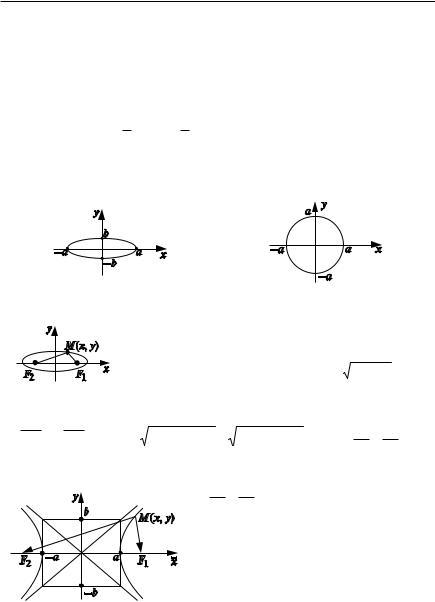
1. Эллипс (pис. 1.25).
x2 |
|
y2 |
1 — центрально симметричная ограниченная кривая |
|
|
2 |
|
||
a |
2 |
|
||
|
|
b |
|
|
с полуосями a и b, пересекающая оси координат в точках (0, / b), (/a, 0). При a b получаем уравнение окружности (pис. 1.26).
Если положить x cos t, y sin t, получим параметрические урав
ab
нения эллипса
x a cos t,
0 t 2'.
y b sin t,
|
M(x, |
M62y) R , |
Рис. 1.26 |
|
|
|
Рис. 1.25 |
|
|
|
|
||
|
Характеристическое |
свойство |
эллипса: |
|||
|
эллипсом называется геометрическое место точек |
|||||
|
|
2 |
сумма расстояний которых от двух |
|||
|
данных точек F1(c, 0), F2( c, 0) (c |
a2 b2 , a b), |
||||
Рис. 1.27 |
называемых |
фокусами, |
есть число |
постоянное, |
||
|
равное 2a (pис. 1.27): |
|
|
|
||
|
|
|
|
|
2 |
2 |
| MF1| | MF2| 2a (c x)2 y2 (c x)2 y2 2a x2 |
y2 1. |
|||||
|
|
|
|
|
a |
b |
2. Гипербола (pис. 1.28). |
Рис. 1.28 |
x2 y2 1 — центрально симмет a2 b2
ричная неограниченная кривая, пересе кающая ось OX в точках (/a, 0), ветви
которой приближаются при x / к
двум прямым |
x |
|
y |
0 и |
x |
|
y |
0, назы |
a |
b |
a |
|
|||||
|
|
|
|
b |
||||
ваемым асимптотами гиперболы.

|
|
|
|
|
1.11. Кривые и поверхности второго порядка |
55 |
||||||||||||
|
|
Характеристическое свойство гиперболы: гиперболой называется |
||||||||||||||||
геометрическое место точек M(x, y) R2 , модуль разности расстояний |
||||||||||||||||||
от которых до двух фиксированных точек F1(c, 0) и |
|
|
||||||||||||||||
F2( c, 0), (c |
a2 b2 ), называемых фокусами, по |
|
|
|||||||||||||||
стоянен и равен 2a. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
| MF1| | MF2| 2a (x c)2 y2 (x c)2 y2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
/2a x2 y2 |
1. |
|
|
|
|
|
|
Рис. 1.29 |
||||||
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|||
x |
y |
1 — сопряженная гипербола (pис. 1.29). |
|
|
||||||||||||||
a |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3. Парабола (pис. 1.30). |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y2 2 px |
— |
симметричная |
относительно |
|
|
|
|
|||||||||
оси OX, неограниченная кривая с вершиной в |
|
|
|
|
||||||||||||||
точке (0, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Характеристическое |
свойство |
параболы: |
|
|
Рис. 1.30 |
|||||||||||
параболой называется геометрическое место |
|
|
|
|
||||||||||||||
точек, равноудаленных от фиксированной точки |
P |
|
||||||||||||||||
F |
, 0 , называе |
|||||||||||||||||
мой фокусом, и |
фиксированной прямой |
P |
|
2 |
|
|||||||||||||
, называемой директ |
||||||||||||||||||
|
|
M62x |
2 |
|||||||||||||||
рисой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
| MF | | MM | |
|
P |
2 |
|
|
P 2 |
|
2 px. |
|||||||
|
|
|
x |
|
|
y2 |
x |
|
|
y2 |
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
4. Пара пересекающихся прямых (pис. 1.31). |
|
|
||||||||||||||
|
|
|
|
|
x2 |
y2 |
0 x y 0, |
|
x y 0. |
|
||||||||
|
|
|
|
|
a2 |
b2 |
|
a |
b |
|
|
a |
b |
|
|
|||
|
|
5. Пара параллельных прямых (pис. 1.32). |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x2 a2 |
|
или |
y2 b2. |
|
|
|
|
||||
|
|
|
|
Рис. 1.31 |
|
|
|
|
|
|
|
|
Рис. 1.32 |
|||||
56 Глава 1. Элементы линейной алгебры и аналитической геометрии
6. Пара совпадающих прямых.
x2 0 — ось OY, или y2 0 — ось OX.
7. Точка.
x2 y2 0 x 0, y 0.
8. Пустое множество.
x2 y2 1 0.
1.11.2. Поверхности второго порядка
ОПРЕДЕЛЕНИЕ 2. Поверхностью второго порядка называется множество всех точек M(x, y, z) R3, удовлетворяющих уравнению a11x2 2a12 xy a22 y2 2a13 xz 2a23 yz a33z2 b1x b2 y b3z b0 0. (2)
Канонические уравнения поверхностей второго порядка
|
|
M62 |
|
|
|||||
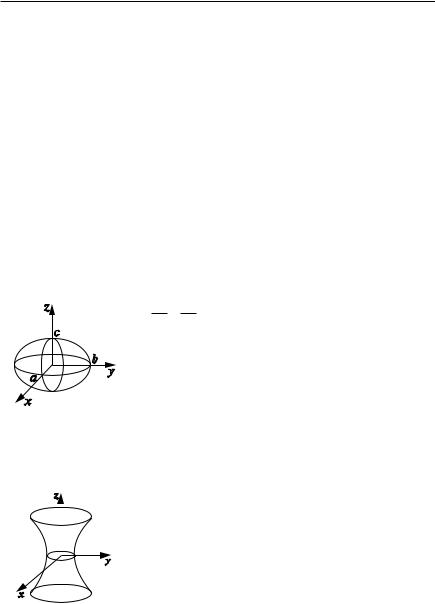
1. Эллипсоид (pис. 1.33). |
|
|
|
|
|
||||
|
x2 |
y2 |
z2 |
1 — |
центрально симметричная |
||||
|
a |
|
2 |
2 |
|
|
|
|
|
|
|
b |
c |
|
|
|
|
||
|
ограниченная |
поверхность, |
пересекающая оси |
||||||
|
координат в точках (/a, 0, 0), (0, / b, 0), (0, 0, / c), ле |
||||||||
|
жащая |
в |
прямоугольном |
параллелепипеде |
|||||
|
a x a, b y b, c z z. Все плоские сече |
||||||||
Рис. 1.33 |
ния эллипсоида являются |
эллипсами. |
При |
||||||
a b c |
получаем |
уравнение |
сферы |
||||||
|
|||||||||
x2 y2 z2 a2 .
2. Гиперболоиды. |
|
|
|
|
|
|
|||
|
|
|
x2 |
|
y2 |
|
z2 |
1 — однополостный гиперболо |
|
|
|
|
|
|
|
|
|||
|
|
|
a |
2 |
2 |
2 |
|
||
|
|
|
|
|
b |
|
c |
||
|
|
ид (pис. 1.34), неограниченная центрально сим |
|||||||
|
|
метричная поверхность. Плоскости z c пересе |
|||||||
|
|
кают его по эллипсам, плоскости x c и y c — |
|||||||
|
|
по гиперболам. Поверхность гиперболоида можно |
|||||||
|
|
составить из прямых. Это свойство однополост |
|||||||
|
|
ного гиперболоида было использовано известным |
|||||||
Рис. 1.34 |
советским инженером Шуховым при строительст |
||||||||
|
|
ве первой московской телебашни. |
|||||||
1.11. Кривые и поверхности второго порядка |
57 |
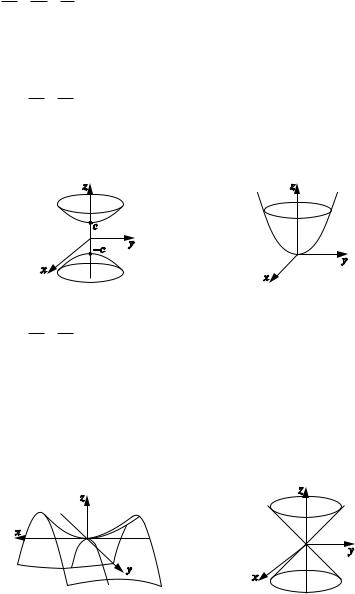
x2 y2 z2 1 — двуполостный гиперболоид (pис. 1.35), неогра a2 b2 c2
ниченная центрально симметричная поверхность. Плоскости z c пе ресекают его по эллипсам, плоскости x c, y c — по гиперболам.
3. Параболоиды.
2z x2 y2 — эллиптический параболоид (p, q 0) (pис. 1.36), не
pq
ограниченная поверхность с осью симметрии Oz, расположенная в по лупространстве z 0. Сечения его плоскостями z c — эллипсы, а x c, y c — параболы.
Рис. 1.35 |
M62 |
Рис. 1.36 |
|
2z x2 y2 — гиперболический параболоид (pис. 1.37), неограни
pq
ченная поверхность с осью симметрии Oz. Сечения его плоскостями
z c — гиперболы, а x c, y c — параболы.
4. |
Конус (pис. 1.38). |
|||||
x2 |
|
y2 |
|
z2 |
0 — неограниченная центрально симметричная по |
|
|
2 |
|
|
|||
a |
2 |
2 |
|
|||
|
|
b |
|
c |
|
|
верхность с центром в начале координат. Сечения его плоскостями z c — эллипсы, x c, y c — гиперболы.
Рис. 1.37 |
Рис. 1.38 |
58 Глава 1. Элементы линейной алгебры и аналитической геометрии
|
|
|
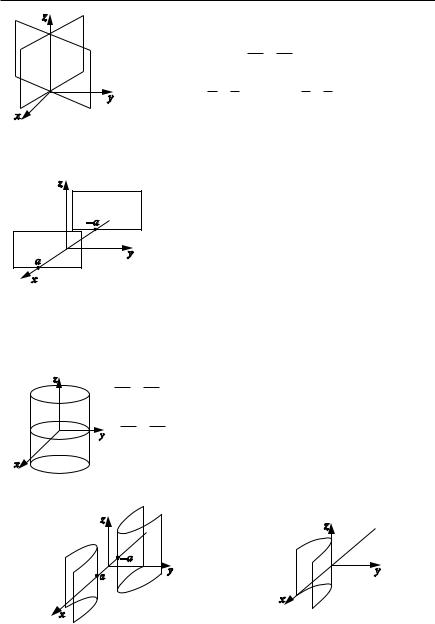
5.Пара пересекающихся плоскостей (pис. 1.39). |
|||||
|
|
|
|
x2 |
y2 |
0. |
|
|
|
|
|
|
a |
2 |
2 |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
x y 0 |
или |
x y 0. |
|
|
|
|
|
|
a b |
|
|
a b |
|
Рис. 1.39 |
|
|
6. Пара параллельных плоскостей (pис. 1.40). |
|||||
|
|
|
|
|
x2 a2. |
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x a, |
|
|
|
|
|
|
|
|
x a. |
|
|
|
|
|
|
7. Пара совпадающих плоскостей. |
||||
|
|
|
|
x2 0 — плоскость yOz. |
||||
|
|
|
|
8. Цилиндры. |
Поверхность |
называется |
||
|
|
|
цилиндрической, если она получена движе |
|||||
|
|
|
нием прямой (образующей) |
параллельно |
||||
Рис. 1.40 |
|
|
фиксированной прямой по плоской кривой |
|||||
|
|
|
(направляющей). |
|
|
|
||
F(x, y) 0 — уравнение цилиндрической поверхности с образую |
||||||||
|
|
|
|
направляющей, лежащей в плоскости xOy |
||||
щей, параллельной оси OzM62и |
|
|
||||||
и задаваемой уравнением F(x, y) 0. |
|
|
|
|
||||
x2 |
|
y2 |
1 — эллиптический цилиндр (pис. 1.41). |
|||||
a |
2 |
|
2 |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
x2 |
y2 |
1 — гиперболический цилиндр (pис. 1.42). |
|||||
a |
2 |
2 |
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
y2 2 px — параболический цилиндр (pис. 1.43).
Рис. 1.41
Рис. 1.42 |
Рис. 1.43 |

|
|
|
|
|
1.12. Классификация кривых и поверхностей второго порядка |
59 |
||||||||||||
|
9. Прямая. |
|
|
|
|
|
|
|
||||||||||
|
x2 |
|
|
y2 |
|
0 x 0, y 0 — ось Oz. |
|
|||||||||||
|
|
2 |
|
|
|
|
||||||||||||
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Точка. |
|
|
|
|
|
|
|
||||||||||
|
x2 |
|
|
y2 |
|
|
z2 |
0 x 0, |
y 0, z 0 — начало координат. |
|
||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||
|
a |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
b |
|
|
|
c |
|
|
|
|
|
|
|
|||
|
11. Пустое множество. |
|
|
|
|
|
|
|||||||||||
|
x2 |
|
|
y2 |
|
|
z2 |
1 или |
|
x2 |
|
y2 |
1. |
|
||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||
|
a |
2 |
2 |
|
|
|
a |
2 |
|
|
||||||||
|
|
|
|
b |
|
|
c |
|
|
|
b |
|
||||||
|
|
|
1.12. Классификация кривых и поверхностей второго порядка |
|
||||||||||||||
|
|
|
Классификация кривых второго порядка. Классификация поверхно |
|
||||||||||||||
|
|
|
стей |
второго порядка |
M62 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1.12.1. Классификация кривых второго порядка |
|
||||||||||
|
Теорема 1. Всякая кривая второго порядка |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a11x2 2a12 xy a22 y2 b1x b2 y b0 0 |
(1) |
||||||
является или эллипсом, или гиперболой, или параболой, или парой пересе2 кающихся прямых, или парой параллельных прямых, или парой совпадаю2 щих прямых, или точкой, или пустым множеством.
Суть доказательства теоремы состоит в переходе к такой прямо угольной системе координат, в которой (1) имеет канонический вид.
Переход к этой системе координат в R2 осуществляется путем по ворота исходной системы координат и ее параллельного переноса.
Сначала рассмотрим частный случай (1), когда a12 0. Для приве дения (1) к каноническому виду достаточно выделить полные квадра ты отдельно у членов, содержащих x и y.

60Глава 1. Элементы линейной алгебры и аналитической геометрии
Пр и м е р. x2 4х 4y2 8y 8 0 (x2 4x) 4(y2 2 y) 8 0
(x2 2 2 x 4 4) 4(y2 2 y 1 1 1) 8 0 (x 2)2 4(y 1)2 16
(x 2)2 (y 1)2 1. 42 22
Впоследнем уравнении сделаем замену
x x 2,
y y 1,
т. е. с помощью параллельного переноса перейдем к новой системе координат с центром в точке O (2, 1). В этой системе координат урав нение рассматриваемой кривой примет канонический вид
|
|
(x )2 |
|
(y )2 |
|
|||
|
|
|
|
|
|
1. |
|
|
|
|
2 |
|
2 |
2 |
|
||
|
4 |
|
|
|
|
|
||
Это эллипс с полуосями |
M62 |
|
||||||
a 4, b 2. |
|
|
||||||
При рассмотрении общего случая исследуем квадратичную форму |
||||||||
a x 2a |
yx a y2 |
(2) |
||||||
|
11 |
|
12 |
|
|
|
||
и постараемся избавиться от произведения xy.
По квадратичной форме (2) выпишем симметричную матрицу
|
|
a |
a |
|
|
|
|
|
A 11 |
12 |
, |
|
|
|
|
|
|
a12 |
a22 |
|
|
|
|
которая в R2 определяет самосопряженный |
оператор. Оператор А |
||||||
и квадратичная форма связаны соотношением |
|
||||||
a11x2 2a12 xy a22 y2 |
|
x |
|
x |
|||
A |
|
, |
. |
||||
|
|
|
|
|
y |
|
y |
Действительно, |
|
|
|
|
|
|
|
|
x x |
a |
a |
x |
x |
||
A |
, |
11 |
12 |
, |
|
|
|
|
y y a12 a22 y |
y |
|||||
(a11x a12 y)x (a12 x a22 y)y a11x2 2a12 xy a22 y2.
