
Основы высшей математики для инженеров 2009
.pdf
1.8. Метод Гаусса практического решения систем линейных уравнений |
41 |
При вычислении ранга матрицы полезно пользоваться элементар ными преобразованиями как над строками, так и над столбцами.
П р и м е р. Определить ранг матрицы
|
3 |
5 |
7 |
|
|
|
|
A |
1 |
2 |
3 . |
|
|
3 |
|
|
1 |
5 |
Вычислим определитель данной матрицы путем разложения по элементам первой строки. При этом воспользуемся отмеченной здесь связью между минорами и алгебраическими дополнениями:
det A a M1 |
a |
M1 |
a |
M1 |
3 |
2 |
3 |
5 |
1 |
3 |
7 |
1 |
2 |
3 1 5 2 7 1 0. |
|
11 |
1 |
12 |
2 |
13 |
3 |
|
3 |
5 |
|
1 |
5 |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Как видим, определитель данной матрицы равен нулю, но миноры второго порядка отличны от нуля. Следовательно, ранг матрицы А: rang A 2.
1.8.3. ТеоремаM62Кронекера – Капелли
Система (1) совместна, т. е. имеет хотя бы одно решение, тогда
итолько тогда, когда rang A rang A1, причем
1)если rang A rang A1, то (1) несовместна;
2)если rang A rang A1 r n (числу неизвестных), то (1) неопре2 деленна;
3)если rang A rang A1 n, то (1) имеет единственное решение.
Отметим, что однородная система всегда совместна, так как имеет нулевое решение. Для нее справедливо
СЛЕДСТВИЕ. Размерность пространства решений ker A однород ной линейной системы Ax 0 равна n r.
Из сформулированной теоремы вытекает алгоритм решения сис темы (4).
Пусть rang A rang A1. В матрице А выделяем базисный минор по рядка r. С этим минором связаны r уравнений и r неизвестных систе мы (1). Эти уравнения и неизвестные назовем базисными; все осталь ные уравнения системы отбросим, а все остальные n r неизвестных в базисных уравнениях перенесем направо. Получим систему из r ба зисных уравнений с r базисными неизвестными. Так как ее определи тель, являясь базисным минором, отличен от 0, то по правилу Краме ра полученная система имеет единственное решение. Это решение,

42 Глава 1. Элементы линейной алгебры и аналитической геометрии
зависящее от n r произвольных постоянных, соответствующих неба зисным неизвестным, и будет общим решением исходной системы (1). Этот алгоритм мы будем применять к эквивалентной ступенчатой сис теме, полученной из исходной с помощью метода Гаусса.
П р и м е р. Найти размерность и базис пространства решений од нородной линейной системы
x1 x2 3x3 2 x4 0,
&
2 x1 3x2 x3 x4 0, &4x1 x2 5x3 3x4 0.
Решение. Составляем расширенную матрицу |
||||||
|
1 |
1 |
3 |
2 |
|
0 |
|
|
|||||
A1 |
|
|
|
|
|
|
2 3 1 1 |
|
0 . |
||||
|
|
1 |
5 |
3 |
|
|
|
4 |
|
0 |
|||
2, а к третьей — первую,M62 |
|
4: |
||||
С помощью метода Гаусса преобразуем эту матрицу к ступенчатому виду. Для этого прибавим ко второй строке первую, умноженную на
|
умноженную на |
|||||
|
1 |
1 |
3 |
2 |
|
0 |
|
|
|||||
A1 ~ |
|
|
|
|
|
|
0 5 7 |
5 |
|
0 . |
|||
|
|
5 |
7 |
5 |
|
|
|
0 |
|
0 |
|||
Прибавим к третьей строке вторую, умноженную на 1, и отбросив нулевую строку, получим ступенчатую матрицу
|
1 |
1 |
3 |
2 |
0 |
1 |
1 |
3 |
2 |
|
0 |
A |
|
|
|
5 |
|
|
|||||
~ 0 5 7 |
0 ~ |
|
|
|
|
. |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
5 |
7 |
5 |
|
0 |
|
|
||||||||||
|
0 |
0 |
|
|
|
|
|
|
|||
Так как минор
1 1
5 0,
0 5
то rang A rang A1 2.

1.9. Линейные операторы |
43 |
Полученной матрице соответствует система
1 x2 3x3 2 x4 0,
5x2 7x3 5x4 0.
Вкачестве базисных неизвестных возьмем x1 и x2 . Тогда
8
&x3 x4,&x1 5
&&x2 7 x3 x4.5
Это и есть общее решение системы, зависящее от двух произвольных постоянных x3, x4. Положим x3 u, x4 v и запишем его так:
|
|
|
|
|
|
8 |
u v |
8 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
5 |
|
|
5 |
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
||
|
|
x |
|
7 |
|
|
|
7 |
|
|
|
||||
|
|
2 |
|
M62 |
|
|
|||||||||
|
|
|
|
||||||||||||
x |
|
|
u v |
u |
|
|
v |
|
, u, v R. |
||||||
x |
|
|
|
0 |
|||||||||||
|
|
|
5 |
|
|
5 |
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
x4 |
|
u |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
Окончательно, пространство решений — это двумерное простран
ство (двумерная плоскость в R4) с базисом |
|
|
|
8 |
, |
7 |
, 1, |
|
и |
|
|
|
|
||||||||
a |
|
|
|
0 |
||||||
|
|
|||||||||
|
1 |
5 |
|
5 |
|
|
|
|||
|
|
|
|
|
|
|
||||
a2 ( 1, 1, 0, 1).
1.9. Линейные операторы
Определение и примеры линейных операторов. Матрица линейного оператора. Самосопряженный оператор. Действия над линейными опе раторами.
1.9.1.Определение и примеры линейных операторов
Вматематическом анализе изучаются функции, аргументом и зна чением которых являются действительные числа. Мы будем изучать функции, аргументом и значением которых будут векторы n мерного

44 Глава 1. Элементы линейной алгебры и аналитической геометрии
линейного пространства Rn. При этом мы ограничимся простейшим типом таких функций, а именно линейными, которые будем называть линейными преобразованиями или линейными операторами. Линей ные операторы имеют особое значение в линейной алгебре и ее при ложениях.
ОПРЕДЕЛЕНИЕ 1. Пусть каждому вектору x Rn поставлен в со ответствие единственный вектор y Rn. Функция y A(x) называется преобразованием или оператором из Rn в Rn. При этом вектор x назы вается прообразом, а y — образом оператора.
Оператор А называется линейным, если x1, x2 Rn, R выпол няются равенства:
1)A(x1 x2) Ax1 Ax2,
2)A( x1) Ax1.
П р и м е р ы.
1. Тождественный (или единичный) оператор — это линейный оператор, действующий по правилу
2. Оператор подобия. Пусть k R, x R ,
M62I x x. n
Ax kx.
Оператор А линейный:
A(x1 x2) k(x1 x2) kx1 kx2 Ax1 Ax2;
A( x1) k( x1) (kx1) Ax1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Оператор сдвига на вектор: Ax |
x x0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Он является |
линейным тогда и только тогда, |
когда |
|
0 |
0, т. е. |
||||||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ax |
x. В самом деле, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
A( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2) x1 x2 x0 Ax1 Ax2 x1 x2 2 x0 x0 0. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
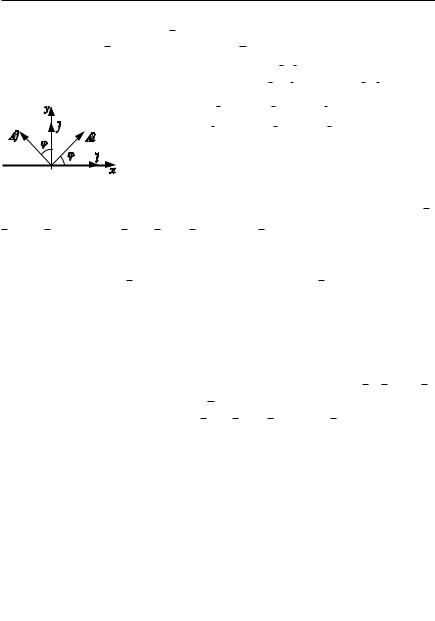
4. Оператор поворота в R2 на угол ( вокруг начала координат |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
(pис. 1.23). Этот |
|
оператор является линейным. |
В самом |
|
деле, |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
снача |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2) означает, что векторы x1 и x2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ла складываются, а затем их сумма поворачи |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вается на угол (. Сумма означает, что векторы |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 и x2 сначала поворачиваются на угол (, а |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
затем складываются. Ясно, что результат один |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и тот же. Аналогично проверяется равенство |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Рис. 1.23 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x1) Ax1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||

1.9. Линейные операторы |
45 |
1.9.2. Матрица линейного оператора
ОПРЕДЕЛЕНИЕ 2. Пусть e1, e2 , …, en — базис (не обязательно ор тонормированный) в Rn; A : Rn Rn — линейный оператор, Ae1, Ae2 , …, Aen — образы базисных векторов. Так как эти образы лежат в Rn, то их можно разложить по этому базису, т. е. записать в виде
Ae1 a11e1 a21e2 an1en;
Ae2 a12 e1 a22 e2 an2 en;
. . . . . . . . . . . . . . . . . . . .
Aen a1ne1 a2ne2 annen.
Образуем квадратную матрицу порядка n:
a11 |
a12 |
|
a1n |
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
a2n |
|
|
|
(1) |
|
|
|
. |
|
|
|
|
|
an |
|
|
|
|
|
|
an1 |
|
ann |
|
|
|
|
|
M62 |
1 |
2 |
n |
А, называется |
|||
Эта матрица, которую мы тоже будем обозначать через |
|||||||
матрицей линейного оператора А в базисе e , e , …, e .
1. Матрица тождественного оператора Ax x:
|
|
|
|
|
|
|
||
Ae1 e1 |
1 0 |
0 |
||||||
|
|
|
|
|
|
|
|
|
Ae |
|
e |
0 |
1 |
0 |
|||
2 |
2 |
A |
|
E. |
||||
. . . . . . |
||||||||
|
|
|
|
|
|
|
|
|
Aen en |
0 |
0 |
1 |
|||||
2. Матрица оператора подобия Ax kx:
|
|
|
|
|
|
|
|
|
Ae1 |
ke1 |
k |
0 |
|
||||
|
|
|
|
|
|
|
|
|
Ae |
|
ke |
0 |
k |
|
|||
2 |
|
2 A |
|
|
|
|||
. . . . . . |
|
|
||||||
|
|
|
|
|
|
|
|
|
Aen ken |
0 |
0 |
|
|||||
0kE.
k
3. Оператор с матрицей в некотором базисе e1, e2 , …, en вида
|
1 |
0 |
|
0 |
|
|
|
|
0 |
2 |
|
0 |
|
A |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
0 |
|
|
|
|
|
|
2 |
|||
46 Глава 1. Элементы линейной алгебры и аналитической геометрии
называется диагональным. Его геометрический смысл состоит в том, что он растягивает вектор x по осям координат в 1, 2 , …, n, соот ветственно раз: x (x1, x2, , xn) Ax ( 1x1, 2 x2, , n xn).
4. Матрица оператора поворота. Пусть 0, i , j — прямоугольная сис тема координат в R2 (pис. 1.24). Разлагая Ai , Aj по базису i , j получим
|
|
|
|
|
Ai cos ( i |
sin ( j, |
||||
|
|
|
|
|
Aj sin ( i |
|
|
|
||
|
|
|
|
|
cos ( j, |
|||||
|
|
|
|
|
A |
cos ( |
|
sin ( |
||
|
|
|
|
|
|
|
|
|
. |
|
|
Pис. 1.24 |
|
|
|
|
sin ( |
cos ( |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1. Если (1) |
— матрица линейного оператора А в базисе e1, |
||||||||
e |
, …, e , то для x x e x e |
x e Rn |
||||||||
2 |
n |
1 1 |
2 2 |
|
|
n n |
|
|
|
|
|
|
a11 |
a12 |
a1n x1 |
|
|||||
|
A(x) |
a |
a |
|
a |
x |
|
|||
|
|
21 |
22 |
|
2n |
|
2 |
Ax. |
||
|
|
|
M62 |
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
an |
|
|
|
|
|
|
|
|
an1 |
ann xn |
|||||||
Данное утверждение открывает широкие возможности практиче ской реализации преобразования векторных величин. Поэтому раскро ем его содержание без использования математической символики.
Если (1) есть матрица линейного преобразования А а базисе e1, е2 , …, еп, то преобразование любого вектора х, представленного в данном простран2 стве в виде разложения по базису x x1e1 x2 e2 xnen , можно осуще2 ствить путем умножения матрицы А на вектор2столбец из заданных коор2 динат данного вектора.
Сказанное подтверждается приведенными выше примерами. В об щем виде рассмотрим доказательство для двумерного пространства.
Доказательство. Пусть n 2 и A : R2 R2 , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
в базисе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из свойств линейности |
|
|
|
|
|||||||||||||||||
e1, e2 . Тогда x x1e1 x2 e2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Ax |
A(x1e1 x2 e2) x1Ae1 x2 Ae2 x1(a11e1 a21e2) x2(a12 e1 a22 e2) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x |
a x |
|
a |
|
a |
x |
|
|||||||
(x a |
x a ) |
e |
|
(x a |
x a ) |
e |
|
|
11 1 |
12 2 |
|
11 |
12 |
1 |
. |
||||||||||||||||||||||||
1 |
11 |
2 |
12 |
1 |
1 |
21 |
2 |
22 |
|
2 |
|
a21x1 a22 x2 a21 a22 x2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||

1.9. Линейные операторы |
47 |
Итак, при преобразовании вектора, заданного координатами в не котором базисе, линейным оператором матрица оператора в этом ба зисе умножается на вектор столбец из координат.
1.9.3. Самонапряженный оператор
ОПРЕДЕЛЕНИЕ 3. Линейный оператор A : Rn Rn называется самонапряженным, если в ортонормированном базисе его матрица
A (aij)n!n является симметричной, т. е. aij |
a ji для всех i, j. |
|||||||||||||||||||||||||||
Теорема 2. Если A : Rn Rn — самосопряженный линейный оператор, |
||||||||||||||||||||||||||||
то |
|
, |
|
Rn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
y |
|
|
|
, |
|
|
) ( |
|
|
|
), |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(Ax |
|
y |
x |
, Ay |
|
|
|
|
|
|
|
||||||||
где ( , ) — скалярное произведение в Rn. |
|
|
|
|
|
|
||||||||||||||||||||||
Доказательство для n 2. Пусть в ортонормированном базисе i, j |
||||||||||||||||||||||||||||
R2 матрица оператора А симметричная, т. е. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 11 |
12 , |
|
x |
x i x j, |
y |
y i y j. |
y |
||||||||||||||
|
|
|
|
|
|
|
a |
a M62x y a |
x |
a |
x |
|||||||||||||||||
|
|
|
|
|
|
|
a12 |
a22 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
a11x1 |
a12 x2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
a11 |
a12 |
x1 |
|
|
|
y1 |
y1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
(Ax, y) |
|
|
|
, |
|
|
|
|
, |
|
|
|||||||||||||||
12 |
22 |
2 |
|
|
2 |
12 |
1 |
22 |
2 |
2 |
|
|||||||||||||||||
(a11x1 a12 x2)y1 (a12 x1 a22 x2)y1 (a11y1 a12 y2)x1 (a12 y1 a22 y2)x2
x1 |
|
, |
a11y1 |
a12 y2 |
|
x1 |
|
, |
a11 |
a12 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, Ay). |
|||||||
x2 |
|
|
a12 y1 |
a22 y2 |
x2 |
|
|
a12 |
a22 y2 |
|
||||||
1.9.4.Действия над операторами
1.Сложение операторов. Суммой линейных операторов А и В в Rn
называется линейный оператор C A B такой, что для x Rn
Cx (A B)x Ax Bx.
Нетрудно показать, что матрица оператора С в некотором базисе равна сумме матриц операторов А и В в этом базисе.
2. Умножение оператора на число. Произведением линейного опе
ратора А на число R называется линейный оператор B A такой, что для x Rn
Bx ( A)x (Ax)..
Матрица оператора A равна произведению на матрицу оператора А.

48Глава 1. Элементы линейной алгебры и аналитической геометрии
3.Умножение операторов. Произведением линейных операторов А
иВ называется линейный оператор C AB такой, что для x Rn
Cx (AB)x A(Bx),
т. е. сначала вектор x преобразуется в вектор y Bx, а затем — в век тор z Ay.
При перемножении операторов их матрицы перемножаются. По этому в общем случае AB BA.
Задача. Даны два линейных преобразования:
x1 5x1 x2 3x3, |
x1 2 x1 x3, |
|
|||
& |
2 x2, |
& |
|
, |
|
x2 x1 |
x2 x2 5x3 |
||||
&x 7x |
x ; |
&x 2 x . |
|
||
3 |
2 |
3 |
3 |
1 |
|
Средствами матричного исчисления найти преобразование, выражаю щее x1, x2, x3 через x1, x2, x3.
Решение. Перепишем каждоеM62из преобразований в матричном виде: x Bx, x Ax . Отсюда x Ax ABx. Следовательно, нужно найти матрицу произведения операторов АВ:
|
2 |
0 1 5 1 3 |
|
10 |
5 |
5 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
0 1 |
5 1 |
2 0 |
|
|
|
1 37 |
5 . |
||||
|
|
0 |
0 |
|
7 |
|
|
|
|
|
2 |
|
|
2 |
0 |
1 |
|
10 |
6 |
||||||
Поэтому |
|
|
|
|
|
x1 |
|
10 5 |
5 x1 |
|
|
|
|
|
|
|
|
x2 |
|
1 37 |
5 x2 |
. |
|
|
|
|
|
|
|
x3 |
|
10 2 |
6 x3 |
|
|
4. Обратный оператор. Линейный оператор A 1 называется обрат ным к линейному оператору А, если A A 1 A 1 A E.
Матрица оператора A 1 является обратной к матрице оператора А.

1.10. Собственные векторы и собственные значения линейного оператора 49
1.10.Собственные векторы и собственные значения линейного оператора
Собственные векторы и собственные значения линейного оператора. Условие диагональности линейного оператора. Диагональность само сопряженного оператора.
1.10.1. Собственные векторы и собственные значения линейного оператора
Ненулевой вектор x Rn называется собственным вектором ли нейного оператора А, если существует такое число , что выполняется равенство Ax x. Число называется собственным значением опера тора А, отвечающим собственному вектору x.
Множество собственных значений линейного оператора называет ся его спектром.
Рассмотрим матрицу оператора в некотором базисе:
M62a a a |
|
||||
|
a11 |
a12 |
|
a1n |
|
|
|
|
|
|
|
A |
a21 |
a22 |
a n . |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
n2 |
|
nn |
|
Тогда соотношение Ax x или (A E)x 0 эквивалентно следующему:
a11 |
a12 |
|
a1n |
x1 |
|
|
0 |
|
|
a21 |
a22 |
a2n |
|
|
|
|
|
|
x2 |
|
0 . |
|||||
|
|
|
|
|
|
|
||
|
an1 |
an2 |
|
|
|
|
|
|
|
ann xn |
|
0 |
|||||
Это есть однородная система n го порядка, всегда имеющая нулевое
решение x 0. По правилу Крамера она будет иметь ненулевое реше ние тогда и только тогда, когда ее определитель равен 0, т. е.
a11 |
a12 |
|
a1n |
|
|
|
a21 |
a22 |
|
a2n |
0. |
(1) |
|
|
|
|
|
|||
|
|
|||||
an1 |
an2 |
ann |
|
|
||
Итак, собственные числа являются корнями алгебраического урав нения n го порядка (1), которое называется характеристическим

50 Глава 1. Элементы линейной алгебры и аналитической геометрии
уравнением, а его левая часть — характеристическим многочленом. Заметим, что собственные значения не зависят от выбора базиса, в ко тором записывается матрица оператора А.
Пусть 0 — собственное значение, т. е. решение характеристиче ского уравнения (1). Тогда собственный вектор x, отвечающий этому собственному значению, будет решением однородной системы
(a11 0)x1 a12 x2 a1n xn 0,
& |
(a |
|
|
)x a |
x |
0, |
||||
&a x |
|
0 |
||||||||
21 1 |
|
22 |
|
2 |
|
2n |
|
n |
(2) |
|
&. . . . . . . . . . . . . . . . . . . . . . |
||||||||||
&a x |
a |
n2 |
x (a |
nn |
)x |
0. |
||||
n1 1 |
|
2 |
|
|
|
n |
|
|
||
Так как множество решений линейной однородной системы явля ется линейным пространством, то для нахождения собственных векто ров x, отвечающих собственному значению 0, достаточно методом Гаусса найти базис этого пространства.
П р и м е р. Найти собственные векторы и собственные значения |
||
линейного оператора А |
M628 9 |
|
с матрицей |
|
|
|
5 |
4 |
|
A |
. |
Решение. Составим характеристическое уравнение (1): |
||
5 |
4 |
2 14 13 0. |
|
0 или |
|
89
Собственные значения 1 1, 2 13. Для 1 1 составим систему (2):
|
|
|
|
4x |
4x |
0 |
x x 0 |
x x |
|
x t |
|||||||
|
|
|
|
|
1 |
2 |
|
|
1 |
|
|||||||
|
|
|
|
8x1 8x2 0 |
1 |
2 |
1 |
2 |
|
x2 t |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
x |
|
1 |
— одномерное линейное пространство собственных векто |
||||||||||||||
1 |
|
t |
|
||||||||||||||
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ров с базисом |
|
|
|
|
|
|
|
|
|
||||||||
a1 ( 1, 1). |
|
|
|
|
|
|
|
||||||||||
|
Для 2 13 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
8x |
4x 0 |
2 x |
x |
0 2 x |
x |
|
|
x t |
||||||
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
||||||
|
|
|
8x1 4x2 0 |
1 |
2 |
1 |
2 |
|
x2 |
2t |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
