Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Основы высшей математики для инженеров 2009

.pdf

Скачиваний:

225

Добавлен:

12.03.2016

Размер:

10.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4911 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

не обращается в нуль на (–1, 1). Это вы

2.10. Некоторые теоремы... о дифференцируемых функциях

101

Пусть M m. Пусть f (c) M, где c (a, b), M 0. Тогда f (c -x) f (c) для -x любого знака, так как f (c) — наибольшее значение функции. По этому при -x 0

		f (c -x) f (c)		0.	(1)

		-x
При -x 0
		f (c -x) f (c)		0.	(2)

		-x
Переходя к пределу при -x 0 в (1) и (2), получим
lim	f (c -x) f (c)		f (c) 0,

-x 0		-x
lim	f (c -x) f (c)		f (c) 0.

-x 0		-x

Сравнивая два последнихM62неравенства, видим, что f (c) 0.

Геометрическая интерпретация. Если непрерывная кривая, имею щая в каждой точке (a, b) касательную, пересекает ось OX при x a и x b, то найдется такая точка c (a, b), в которой касательная парал лельна оси OX (рис. 2.18).

Рис. 2.18 Рис. 2.19

З а м е ч а н и е 1. Теорема остается справедливой и в том случае, когда f(a) f(b) 0. Доказательство аналогично.

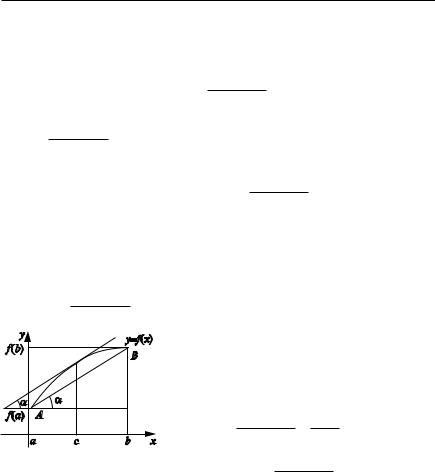
З а м е ч а н и е 2. Требование дифференцируемости функции в точках (a, b) существенно. Например, функция y 1 3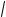x2 непрерывна на ? 1,1@,

2 f ( 1) f (1) 0. Но f (x) 33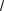x

звано тем, что f (0) не существует (рис. 2.19).

На графике нет точки, в которой касательная параллельна оси OX.

102Глава 2. Дифференциальное исчисление функций одной переменной

2.10.2.Теорема Лагранжа о конечных приращениях

Если f (x) непрерывна на [a, b] и дифференцируема во всех внутренних
точках этого отрезка, то внутри отрезка найдется такая точка c, что
		f (c)	f (b) f (a).	(3)
			b a
Доказательство. Рассмотрим			функцию F(x) f (x) f (a) (x a)Q,
где Q f (b) f (a).
b a	F(a) f (a) f (a) (a a)Q 0;
	F(a) f (a) f (a) (a a)Q 0;
F(b) f (b) f (a) (b a) f (b) f (a) 0.
			b a
F(x) вместе с f (x) дифференцируема на (a, b). Поэтому она удовлетво
ряет всем условиям теоремы Ролля. Следовательно, существует точка
c (a, b) такая, что F (x) 0, но
	F (c) f (c) Q 0 f (c) Q,
т. е. f (c) f (b) f (a).
b a
		Поясним геометрически ход рассуждений
		при доказательстве теоремы. Пусть график
		M62
		f (x) имеет вид, показанный на рис. 2.20. Со
		единим точки A[a, f (a)] и B[b, f (b)] хордой АВ.
		Напишем уравнение прямой АВ:
			y f (a) x a
			f (b) f (a)	b a
Рис. 2.20			y f (a) f (b) f (a) (x a).
			y f (a) f (b) f (a) (x a).
			b a
Если из ординат графика функции y f (x) при x вычесть ординаты
прямой АВ, то получим новую функцию, обращающуюся в нуль при
x a и x b. Это и есть F(x). Из рисунка ясно, что Q — тангенс угла
наклона хорды к оси OX. Поэтому теорема Лагранжа утверждает, что
на [a, b] найдется такая точка, что касательная к графику функции
в этой точке параллельна хорде, стягивающей точки А и В.
Формула (3) может быть переписана в виде
		f (b) f (a) f (c)(b a).		(4)

Но F (c) f (c) Q( (c) 0, следовательно,

2.10. Некоторые теоремы... о дифференцируемых функциях

103

Таким образом, приращение дифференцируемой функции на сегмен те [a, b] равно приращению аргумента (длине сегмента), умноженному на значение производной в некоторой точке сегмента (формула Ла гранжа).

П р и м е р. Для отрезка параболы y x2 , заключенного между точ ками A(1, 1) и B(3, 9), найти такую точку на отрезке [1, 3], в которой ка сательная к графику параболы параллельна хорде АВ.

Пользуясь теоремой Лагранжа, можно доказать следующую теорему.

2.10.3. Теорема Коши об отношении приращений двух функций

Если функции f (x) и ((x) непрерывны на [a, b] и дифференцируе мы во всех его внутренних точках, и если при этом ((x) 0 на (a, b),


то найдется такая точка c (a, b), что
	f (b) f (a)	f (c).
		f (c).
	((b) ((a)		((c)
M6f (b)2f (a)				и рассмотрим
Доказательство. Положим Q				и рассмотрим

((b) ((a)

F(x) f (x) f (a) Q[((x) ((a)],

F(a) f (a) f (a) Q[((a) ((a)] 0,

F(b) f (b) f (a) f (b) f (a) [((b) ((a)] 0. ((b) ((a)

Ясно, что функция F(x) непрерывна на [a, b] и дифференцируема во всех его внутренних точках. Поэтому она удовлетворяет всем условиям теоремы Ролля. Следовательно, существует такая точка c, что F (c) 0.

f (c) Q

((c)

f (b) f (a) f (c). ((b) ((a) ((c)

104Глава 2. Дифференциальное исчисление функций одной переменной

2.11.Раскрытие неопределенностей

			. Раскрытие
Правило Лопиталя. Раскрытие неопределенностей вида

неопределенностей вида (0 ) и ( ). Раскрытие неопределенностей вида (00), ( 0), (1 ).

2.11.1. Правило Лопиталя

Пусть функции f (x) и ((x) определены на [a, b] и обращаются в нуль при x x0, т. е. f (x0) ((x0) 0. Тогда при x x0 не определено

отношение f (x), но оно определено в точках, близких к x0. Поэтому ((x)

возникает необходимость вычислить предел lim f (x). Отыскание та

			x x0 ((x)
			0
кого предела называют обычно раскрытием неопределенности типа				.
				.
	0. Тогда,M62		0
Пусть f (a) (a)	0. Тогда,M62
Теорема. Пусть	f	(x) и ((x) — функции, дифференцируемые в некото2

ром интервале (a, b), причем ((x) 0 на (a, b), и непрерывные на [a, b].

(	если существует предел отношения	f (x)
		((x)

при x a 0, то существует и предел отношения функций f (x), и имеет

				((x)
место равенство
lim	f (x)	lim	f (x)	.

x a 0 ((x)		x a 0 ((x)

Доказательство. Из условий теоремы вытекает, что на промежутке [a, x], где a x b, функции удовлетворяют теореме Коши. Поэтому

f (x)

f (x) f (a)

f (c)

((x)

((x) ((a) ((c)

где a c x; c зависит от x, но при x a 0

c a 0. Следовательно,

lim

f (x)

lim

f (c)

lim

f (c)

lim

f (x)

x a 0 ((x)

x a 0 ((c)

x a 0 ((x)

f (x)

Если

— снова неопределенность типа

, то нужно снова приме

((x)

нить правило Лопиталя.

2.11. Раскрытие неопределенностей

105

П р и м е р 1.
lim	1 cos2 x	lim	2 sin 2 x	lim	2 cos2 x	2.

x 0 x2		x 0 2 x		x 0 1

Правило Лопиталя применимо и в том случае, когда lim f (x) 0,

lim ((x) 0.	x

Действительно,

полагая

видим,

что

и, следовательно,

lim

lim (

z 0 z

lim

z 0

(

П р и м е р 2.

M62

sin

cos

lim

lim cos

z 0 при x

lim f (x).

x ((x)

k k. x

2.11.2.Раскрытие неопределенностей вида .

Пусть f (x) и ((x) стремятся к при x a (x ).

Теорема. Пусть функции f (x) и ((x) дифференцируемы в окрестности точки a (при x a) и ((x) 0 в этой окрестности. Пусть lim f (x) ,

					f (x)		x a	f (x)
lim ((x) . Если существует				lim	f (x)	,	то существует и lim	f (x)	и
lim ((x) . Если существует				lim		,	то существует и lim		и
x a f (x)		f (x)		x a ((x)			x a ((x)
lim	lim		.
lim	lim		.
x a ((x)	x a ((x)

Данная теорема доказывается в соответствии с определением пре дела на языке 1 2, с применением формулы Коши к некоторому ма лому промежутку [х, х0], где х0 ) -. В результате простых, но остро умных преобразований, доказывается, что для любого 1 0 найдется такое 2 0, что

f 4x5 K 1 если f 4x5 K 1 при x a 2.
g4x5	g 4x5	2

106 Глава 2. Дифференциальное исчисление функций одной переменной

А это и доказывает требуемое утверждение, если К конечное. Если K , то проведенное доказательство теоремы можно применить и в этом случае, если поменять ролями функции f и g:

lim g 4x5 lim g4x5 0.

x a f 4x5 x a f 4x5

З а м е ч а н и е. Теорема остается справедливой и при x .

П р и м е р 3.

lim

x ex

П р и м е р 4.

a xn

a xn 1

n 1

a n!

lim

n b xn

b xn 1

n b1n!

n 1

2.11.3. Раскрытие неопределенностей вида (0 ) и ( ) Неопределенность (0 )M62.

Под раскрытием такой неопределенности понимают нахождение предела lim [f (x) ((x)], когда lim f (x) 0, lim ((x) .

x a

Воспользуемся очевидным равенством


	7		:		7
	9	1	<		9
lim [f (x) ((x)] lim 9 f (x)				< lim 9((x)
lim [f (x) ((x)] lim 9 f (x)		1		< lim 9((x)
x a	x a 9	1	<		x a 9
	9		<		9
	8	((x) ;			8

f (x) <

;

Таким преобразованием мы сводим неопределенность вида (0 ) к не

	0
определенности		или	.

	0

П р и м е р 5.
lim x ctg 3x lim		x	lim	1		1	.
				3
x 0	x 0 tg 3x x 0				3

cos2 3x

Неопределенность ( ).

Как и в предыдущем случае, неопределенности такого вида можно раскрыть путем предварительного их преобразования к виду 0 или .

Покажем это на примере.

2.11. Раскрытие неопределенностей

107

П р и м е р 6.

sin x 1

cos x

lim

tg x

lim

cos x

0 cos x

0 sin x

2.11.4. Раскрытие неопределенностей вида (00 ), ( 0 ), (1 )

Все эти неопределенности раскрываются путем логарифмирования выражения [f (x)]((x). При этом пользуются очевидным равенством

lim ((x) ln f (x)

lim [f (x)]((x) ex a	.
x a

(00) lim [f (x)]((x),		когда	lim	f (x) 0,
x a			x a
( 0) lim [f (x)]((x),		когда	lim	f (x) ,
П р и м е р 7.	M62
x a			x a
(1 ) lim [f (x)]((x),		когда	lim	f (x) 1,
x a			x a

lim ((x) 0.

x a

lim ((x) 0.

x a

lim ((x) .

x a

							lim [sin x ln x]
lim xsin x lim esin x ln x ex 0								;
x 0	x 0
	lim sin x ln x lim						ln x	0,
	lim sin x ln x lim						1	0,
	x 0			x 0			1
							sin x
	lim xsin x e0 1.
П р и м е р 8.	x 0
П р и м е р 8.					1
					1
	lim (1 x)x					1.
	x
П р и м е р 9.			1 x2
			1 x2
	lim	1				.
	lim	1				.
	x		x

108 Глава 2. Дифференциальное исчисление функций одной переменной

2.12. Формула Тейлора и ее приложения

Формула Тейлора. Применение формулы Тейлора к вычислению значе ний функции. Разложение функций по формуле Тейлора.

2.12.1. Формула Тейлора

Пусть функция f (x) имеет все производные, до порядка n 1 вклю чительно, на некотором промежутке, содержащем точку a. Найдем многочлен Pn(x) степени не выше n, обладающий свойством:

Pn(a) f (a), Pn(a) f (a), Pn(a) f (a), , Pn(n)(a) f (n)(a). (1) Естественно ожидать, что такой многочлен будет в некотором смысле близок к f (x).

Будем искать Pn(x) в виде
Pn(x) c0 c1(x a) c2(x a)2 cn(x a)n,	(2)

где коэффициенты ci подлежат определению так, чтобы выполнялись
P	(x) 2c	3 2cM62(x a) n(n 1)c (x a)n 2,
условия (1). Найдем производные Pn(x):
P	(x) c	2c (x	a) 3c (x a)	nc (x a)n 1,
	1	2	3	n
	2		3	n

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Pn(n) (x) n(n 1)(n 2) 2 1 cn.

И запишем уравнения для определения коэффициентов многочлена:

Pn(a) c0 f (a)					c0 f (a),
Pn(a) c1 f (a)					c1 f (a),
P (a) 2c f (a)				c			f (a)	,
P (a) 2c f (a)				c				,
n	2			2		2!
. . . . . . . . . . . .						2!
. . . . . . . . . . . .				. . . . . . . .
Pn(n)(a) n(n 1) 2 1cn f (n)(a)					cn		f (n)(a)		.
Pn(n)(a) n(n 1) 2 1cn f (n)(a)					cn				.
							n!
Таким образом,		f (a)			f (a)
Pn(x) f (a) f (a)(x a)		f (a)	(x a)2		f (a)	(x a)3
Pn(x) f (a) f (a)(x a)			(x a)2			(x a)3
	2!			3!

f (n)(a)(x a)n. n!

2.12. Формула Тейлора и ее приложения

109

Обозначим через Rn(x) разность f (x) и Pn(x): Rn(x) f (x) Pn(x), рис. 2.21. Тогда f (x) Pn(x) Rn(x) или

f (x) f (a) f (a)(x a) f (a)(x a)2 f n(a)(x a)n Rn(x).
2!	n!

	Rn(x) называется остаточным членом. Для тех x,
	для которых остаточный член мал, многочлен
	Pn(x) дает хорошее приближение функции. По
	грешность от замены функции f (x) многочленом
	Pn(x) в точке x равна значению Rn(x) в этой точке.
	Попытаемся связать Rn(x) и f (x). Будем ис	Рис. 2.21
	кать Rn(x) в виде	Рис. 2.21
	кать Rn(x) в виде

Rn(x) (x a)n 1 Q, (n 1)!

где Q — некоторая величина, которую при заданной структуре оста точного члена нужно определить так, чтобы остаточный член Rn(x) давал верхнюю оценку погрешностиM62при замене данной функции f (x) полученным выше многочленом. Тогда при заданной степени много члена будет известна степень точности приближенного вычисления функции f (x) на отрезке ?a, x@.

При заданной форме остаточного члена формула (3) примет вид

f (x) f (a) f (a)(x a) f (a)(x a)2 f (n)(a)(x a)n

2! n!

(x a)n 1 Q. (n 1)!

Для определения переменной величины Q введем вспомогатель ную функцию

F(t) f (x) f (t) f (t)(x t)	f (n)(t)		n	(x t)n 1
		(x t)			Q,	(4)
	n!
				(n 1)!

которая является функцией погрешностей формулы Тейлора, допол ненной остаточным членом и записанной для некоторой точки t на отрезке ?a, x@. Как следует из формулы (4), на концах данного отрезка F4a5 0, F4x5 0. Следовательно, согласно теореме Ролля, на данном отрезке существует точка A, в которой производная F 4A5 0. Поэтому неизвестную пока величину Q определим из условия равенства нулю этой производной в некоторой промежуточной точке A.

110 Глава 2. Дифференциальное исчисление функций одной переменной

Запишем выражение для производной:

F (t) f (t) f (t)(x t) f (t) f (t)(x t)2 f (t)(x t)

(n 1)(t)

(x t)

(n)(t)

n 1

(x t)n

(n 1)!

После уничтожения подобных членов получим

F (t)

f (n 1)(t)

(x t)

(x t)n

(5)

f (n 1)(A)

(x A)n

F (A)

(x A)

Q 0.

Следовательно, Q f (n 1)(A). Тогда

Rn(x)

(x a)n 1

f (n 1)(A)

(x a)n 1

f (n 1)[a B(x a)],

(n 1)!

где 0 B 1, a A xC

M622!

Говорят, что остаточный член записан в форме Лагранжа. Формула f (x) f (a) f (a)(x a) f (a)(x a) f (n)(a)(x a)n

(x a)n 1 f (n 1)(A), (n 1)!

где a A x, называется формулой Тейлора для функции f (x) с оста точным членом в форме Лагранжа. Если x 0, то формула приобрета ет вид

f (x) f (0) f (0)x	f (0)	2	f	(n)(0)		4	f	(n 1)(A)		n 1
		x			x				x	,
		x		n!	x			(n 1)!	x	,
2!				n!				(n 1)!

где 0 A xC Это формула Маклорена.

2.12.2. Применение формулы Тейлора к вычислению значений функции

1. Разложим по формуле Тейлора функцию ex:

f (x) ex,	f (0) 1,
f (x) ex,	f (0) 1,
. . . . . . .	. . . . . .
f (n)(x) ex,	f (n)(0) 1,

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4911 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.03.2015220.23 Кб63опытная забивка свай.docx
#
29.03.20153.18 Mб281Организация работы по ДТП.docx
#
03.05.20151.72 Mб50Основания и фундаменты.pdf
#
21.11.2018100.35 Кб7Основные инструменты ТРИЗ.doc
#
12.03.20168.49 Mб268Основы архитектуры Лекции Презентация.pdf
#
12.03.201610.04 Mб225Основы высшей математики для инженеров 2009.pdf
#
14.11.2019109.06 Кб1Основы предпр_АСУ очка.doc
#
01.09.201963.34 Кб2основы предпринимательства.docx
#
24.12.201850.18 Кб7ОСНОВЫ СЕРТИФИКАЦИИ.doc
#
24.12.201859.9 Кб6ОСНОВЫ СТАНДАРТИЗАЦИИ.doc
#
12.03.2016155.69 Кб143ответики иогп .docx