
Основы высшей математики для инженеров 2009
.pdf
1.2. Линейные пространства |
11 |
1.2.2. Понятие и свойства линейной зависимости векторов
ОПРЕДЕЛЕНИЕ 2. Выражение вида 1u1 2u2 nun называ ется линейной комбинацией векторов u1, u2 , …, un, где u1, u2 , …, un L,
1, 2, , n R.
Числа 1, 2 , …, n, входящие в линейную комбинацию, называ ются ее коэффициентами.
ОПРЕДЕЛЕНИЕ 3. Векторы u1, u2 , …, un называются линейно за висимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулю; т. е. если существуют такие коэффициен
ты , |
, …, |
|
, что |
|
|
|
|
|
|
|
0 |
и 2 |
2 |
2 |
0. |
||||||
n |
u |
u |
u |
||||||||||||||||||
1 |
2 |
|
1 1 |
2 2 |
|
|
n n |
|
|
1 |
2 |
n |
|
||||||||
В противном случае, т. е. когда |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(1) |
|||||||
|
|
|
|
|
u1 2u2 nun 0 |
|
|
||||||||||||||
только при 1 2 n 0 эти векторы называются линейно неза висимыми.
|
|
|
Так как 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
u1 0 u2 0 un 0, то линейная независимость u1, |
|||||||||||||||||||||||||||||||||||
|
|
|
1. Векторы 0, u1, u2 , …,M62un линейно зависимы: |
|||||||||||||||||||||||||||||||||||
|
u2 |
, … , |
u |
n означает, что представление (1) единственно. |
||||||||||||||||||||||||||||||||||
|
|
|
Свойства линейной зависимости векторов. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u1 0 u2 0 un 0. |
||||||||||||||||||||
|
|
|
2. Если |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
u1, u2 , …, un L — линейно зависимые, un 1 L, то u1, |
|||||||||||||||||||||||||||||||||||
|
|
|
, …, |
|
n, |
|
n 1 — линейно зависимые. |
|||||||||||||||||||||||||||||||
u2 |
u |
u |
||||||||||||||||||||||||||||||||||||
Доказательство. u1, …, un — линейно зависимые. Тогда пусть
1u1 2u2 nun 0, например, при 1 0 1u1 2u2 nun
0 un 1 0, 1 0.
3.Если u1, u2 , …, un L — линейно независимые, то хотя бы один
из них является линейной комбинацией остальных.
Доказательство. |
|
|
|
|
|
|
— линейно |
зависимые |
1 |
|
|
||||||||||||||||||
u1, u2 , …, un |
u1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||
|
u |
|
|
u |
|
0 |
и, например, |
0 |
u |
|
|
|
2 |
|
u |
|
|
|
u |
. |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 2 |
n n |
|
1 |
1 |
|
|
|
2 |
|
|
n |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
4. Если u1, u2 , …, un L — линейно независимые, а u1, u2 , …, un, un 1 — линейно зависимые, то un 1 является линейной комбинацией.
Доказательство. u1 u2 un un 1 — линейно зависимые тогда существует нетривиальная линейная комбинация 1u12u2 nun n 1un 1, равная нулевому вектору. Если n 1 0, то

12 Глава 1. Элементы линейной алгебры и аналитической геометрии
1u1 nun 0 и не все коэффициенты нули, что противоречит ли нейной независимости u1, u2 , …, un. Поэтому при n 1 0
un 1
|
|
|
|
|
|
n |
|
|
|
1 |
|
u |
|
|
|
u |
. |
||
|
|
|
|||||||
n 1 |
1 |
|
n 1 |
n |
|||||
1.2.3. Размерность и базис. Разложение вектора по базису
ОПРЕДЕЛЕНИЕ 4. Если в линейном пространстве L существует n линейно независимых векторов, а любые n 1 векторов линейно зави симые, то линейное пространство называется n мерным. Число n на зывается размерностью пространства и обозначается dim L n.
Итак, размерность линейного пространства — это максимальное число линейно независимых векторов.
ОПРЕДЕЛЕНИЕ 5. Если dim L n, то система из n линейно неза висимых векторов e1, e2 , …, en, заданных в определенном порядке, на зывается базисом пространстваM62L.
Теорема 1. Если dim L n; e1, e , …, en — базис L, то u L можно
единственным способом разложить по базису, т. е. представить в виде линейной комбинации базисных векторов:
|
|
x1 |
|
|
|
|
|
|
(2) |
u |
e1 x2 e2 xnen, xi R. |
||||||||
Доказательство. Существование разложения. Из определений раз мерности и базиса вытекает, что векторы e1, e2 , …, en — линейно неза висимые, а векторы e1, e2 , …, en, u — линейно зависимые. Поэтому в силу свойства линейной зависимости векторов u является линейной комбинацией e1, e2 , …, en:
u x1e1 x2 e2 xnen.
Единственность разложения. Предположим противное, т. е. пусть есть по крайней мере два разложения:
u x1e1 x2 e2 xnen x1e1 x2 e2 xnen
и, например, x1 x1. Тогда x1 x1 0 и
(x1 x1)e1 (xn xn)en 0,
т. е. e1, e2 , …, en — линейно зависимые. Получили противоречие, так как e1, e2 , …, en — базис. Следовательно, разложение единственно.

1.2. Линейные пространства |
13 |
Числа x1, …, xn в (2) называются координатами вектора u в базисе e1, e2 , …, en. Мы будем писать u (x1, x2, , xn).
Если u (x1, x2, , xn), v (y1, y2, , yn) то из (2) вытекает, что:
1)u v x1 y1, , xn yn;
2)u v (x1 y1, , xn yn);
3)u ( x1, x2, , xn).
Набор из n координат (x1, x2, , xn) мы можем считать вектором арифметического пространства Rn. Поэтому разложение (2) устанав ливает взаимно однозначное соответствие между произвольным ли нейным пространством L размерности n и Rn. Таким образом, мы мо жем отождествлять различные линейные пространства одинаковой размерности.
Охарактеризуем размерность и базисы в рассмотренных нами при мерах линейных пространств.
1. L R — очевидно, dim R 1 и базис образует любое действитель
ное число 0. |
M62 n |
||||||||
1 |
|
||||||||
2. L Rn |
— можно показать, что dim Rn |
n и базис образуют, на |
|||||||
пример, векторы |
|
|
|
|
|
|
|||
|
|
|
(1, 0, , 0), |
|
(0, 1, , 0), |
|
|
(0, 0, , 1). |
|
|
e |
e |
e |
||||||
3. Теорема 2. dim L2 2 и базис L2 образуют любые два неколлинеар2 ных вектора.
Доказательство. Если два вектора a, b коллинеарны, то существу ет действительное число такое, что a b. Следовательно,
ab 0
ивекторы a, b — линейно зависимые. Поэтому два коллинеарных вектора не могут быть базисом в пространстве L2 (на плоскости).
Но на плоскости есть, по крайней мере, два вектора, которые ли нейно независимые и, следовательно, неколлинеарные. Покажем те перь, что любые 3 вектора линейно зависимы. Если среди векторов a, b, c первые два линейно зависимые, то из свойства 2 линейной зави симости вытекает, что и 3 вектора линейно зависимы. Если a, b — ли
нейно независимые, т.е. неколлинеарные, то по теореме 1
c xa yb, xa yb 1 c 0,
и векторы a, b, c — линейно зависимые. Теорема доказана. Аналогично доказывается
Теорема 3. dim L3 3 и базис в L3 образуют любые 3 некомпланарных
вектора.

14 Глава 1. Элементы линейной алгебры и аналитической геометрии
П р и м е р. Проверить, что векторы a (2, 3), b (1, 2) образуют базис в R2 и найти разложение вектора c (9, 4) по этому базису.
1.3. Евклидовы пространства
Скалярное произведение в линейном пространстве. Длина вектора. Угол между векторами. Ортонормированный базис. Скалярное произ
ведение в L3 .
1.3.1. Скалярное произведение в линейном пространстве. Длина вектора. Угол между векторами
ОПРЕДЕЛЕНИЕ 1. Скалярным произведением в линейном про странстве L называется числовая функция, определенная для любых пар векторов u, v L, которую обозначим через (u, v), удовлетворяю щая аксиомам:
1)(u, v) (v, u); M62
2)(u1 u2, v) (u1, v) (u , v);
3)( u, v) (u, v); R;
4)(u, u) 0, (u, u) 0 u 0.
ОПРЕДЕЛЕНИЕ 2. Линейное пространство со скалярным произ ведением называется евклидовым. Евклидово пространство будем обо значать Е.
ОПРЕДЕЛЕНИЕ 3. Длиной вектора u E называется неотрица тельное число
|u | 
 (u, u).
(u, u).
Вектор, длина которого равна 1, называется единичным или нормиро u
|u |
Теорема 1. Для любых 2 векторов u, v E справедливы неравенства:
1)|(u, v)| |u | | v| (неравенство Коши – Буняковского);
2)|u v| |u | | v| (неравенство треугольника).
Доказательство. 1. Рассмотрим неотрицательную числовую функ цию параметра t
0 f (t)  tu v
tu v  2 (tu v, tu v) t2|u |2 2(u, v)t | v|2 .
2 (tu v, tu v) t2|u |2 2(u, v)t | v|2 .

1.3. Евклидовы пространства |
15 |
Так как это есть квадратный трехчлен, неотрицательный для t R, то его дискриминант неположителен:
D 4(u, v)2 4|u |2 | v |2 0.
Отсюда вытекает неравенство Коши – Буняковского |(u, v)| |u | | v| .
2. Из свойств скалярного произведения и неравенства 1)
|u v|2 (u v, u v) |u |2 2(u, v) | v|2 |u |2 2|u | | v| | v|2 (|u | | v|)2.
Поэтому
|u v| |u | | v|.
Неравенство Коши – Буняковского равносильно неравенствам |
|||||||||||
1 |
( |
|
|
, |
|
|
|
|
) |
1, |
|
u |
v |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
| |
|
| |
| |
|
| |
|
|||||
u |
v |
||||||||||
которые позволяют дать определение 4. ОПРЕДЕЛЕНИЕ 4. Если u, v E, то
M6cos (u,^v) (u2, v) .
|u | | v|
1.3.2. Ортонормированный базис
ОПРЕДЕЛЕНИЕ 5. Будем говорить, что n векторов e1, e2 , …, en в n мерном пространстве Е образуют ортогональный базис, если они нормированные и попарно ортогональны, т. е.
|
|
|
|
1, |
i k, |
(ei, ek) |
i k. |
||||
|
|
|
|
0, |
|
Для того чтобы данное определение было корректным, необходи |
|||||
мо доказать, что входящие в определение векторы e1, e2 , …, en действи тельно образуют базис, т. е. линейно независимы. Покажем, что ра венство
1 |
|
|
|
|
|
|
(1) |
e1 2 e2 nen 0 |
|||||||
возможно лишь при 1 2 n 0. Умножая обе части равенст ва (1) скалярно на e1, получаем
1(e1, e1) 2 (e1, e2) n (e1, en) 0,
| | |
| | |
| | |
1 |
0 |
0 |
т. е. 1 0. Аналогично показывается, что и остальные коэффициенты равны 0.

16 Глава 1. Элементы линейной алгебры и аналитической геометрии
Можно доказать, что, используя любую систему из n линейно не зависимых векторов, можно построить ортонормированный базис n мерного евклидова пространства. Процесс ортогонализации произ вольной независимой системы был предложен немецким математиком Шмидтом (начало XX в.).
Выясним, какие удобства имеет ортонормированный базис по сравнению с неортогональным.
Теорема 2. Если e1, e2 , …, en — ортонормированный базис простран2 ства Е, то относительно этого базиса:
1)скалярное произведение двух векторов равно сумме произведений их соответствующих координат;
2)координаты вектора равны скалярным произведениям этого век2 тора на соответствующие базисные векторы.
Доказательство. 1. u x1e1 xnen, v y1e1 ynen, следова тельно,
(u, v) (x1e1 xnen, y1M62e1 ynen) x1y1(e1, e1) x2 y1(e2, e1)
xn y1(en, e1) x1y2(e1, e ) x2 y2(e2, e ) xn y2(en, e2)
x1yn(e1, en) x2 yn(e2, en) xn yn (en, en) x1y1 x2 y2 xn yn,
|
|
|
|
|
| | |
так как |
1 |
||||
|
|||||
( |
|
|
|
|
при i j; |
eiej) 0, |
|||||
( |
|
|
|
|
при i j. |
eiej) 1, |
|||||
Итак,
(u, v) x1y1 x2 y2 xn yn.
2. Умножая обе части равенства u x1e1 x2 e2 xnen на вектор e1 скалярно, получим
(u, e1) x1(e1, e1) x2(e2, e1) xn(en, e1) x1,
так как (e1, e1) 1.
Аналогично показывается, что
x2 (u, e2), , xn (u, en).
Скалярное произведение вектора u на вектор e единичной длины ес тественно назвать проекцией вектора u на вектор e.
1.3. Евклидовы пространства |
17 |
Доказанное утверждение означает, что в ортонормированном ба зисе координаты вектора являются проекциями этого вектора на ба зисные.
Следствие. Если в ортонормированном базисе
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
(x1, x2, , xn), |
|
v |
|
(y1, y2, , yn), |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1y1 x2 y2 xn yn |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|u | |
|
|
|
x1 |
|
x2 |
xn |
, |
|
|
|
cos (u, v) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
x12 xn2 y12 yn2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3.3. Скалярное произведение в L3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ОПРЕДЕЛЕНИЕ 6. |
Скалярным |
|
|
|
|
произведением |
двух векторов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
L3 |
|
называется число ( |
|
|
|
|
|
|
|
) | |
|
|
|
|
|
|
|
| cos ( |
|
,^b |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
, b |
, b |
| |b |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
a |
a |
a |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Проверим выполнение аксиом скалярного произведения. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1. ( |
|
, |
|
|
|
|
|
|
, |
|
|
) — очевидно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
b |
) (b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2. (a1 a2, b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
M62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, b) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(a1, b) |
(a2, b) | a1 a | |b| cos (a1 ^a2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|||||
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |b| cos ( |
|
|
, |
b) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
a1| |b| cos (a1, b) | a2 |
a |
a1 a2| cos (a1 a2, b) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1| cos (a1, b) | a2| cos (a2, b). |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
^
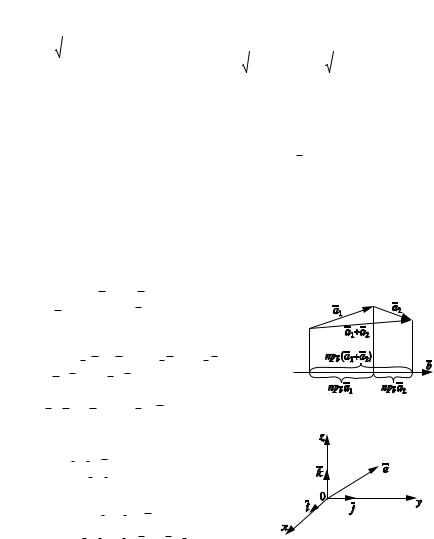
Произведение | a| cos (a, b) назовем проекцией вектора a на вектор b (pис. 1.6).
Тогда (2) немедленно вытекает из рис. 1.6 и равенства
npb(a1 a2) npb a1 npb a2.
3. |
( a, b) (a, b) — доказать |
самостоя |
|
тельно, разбирая отдельно случаи 0, 0. |
|||
4. |
(a, a) | a|2 0, |
a 0. |
Pис. 1.6 |
Пространство L3 |
с введенным скаляр |
||
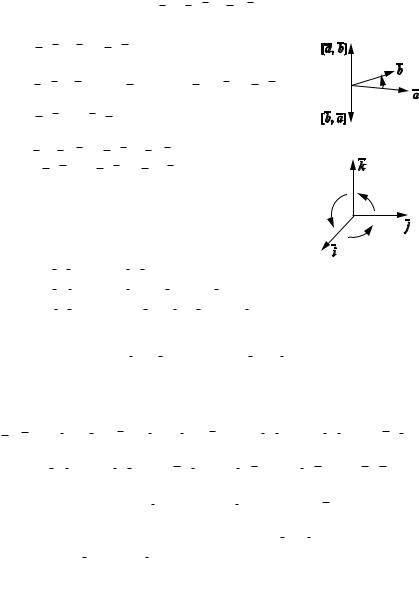
ным произведением обозначим через R3. Пусть i, j, k — ортонормированный
базис в R3; 0, i, j, k — прямоугольная сис тема координат (pис. 1.7),
|i | | j| | k | 1,
i j, j k, k i. Pис. 1.7

18 Глава 1. Элементы линейной алгебры и аналитической геометрии
Координаты вектора a (x, y, z) — это проекции a на оси ко ординат.
Основные формулы в координатах:
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
(x1, y1, z1), b (x2, y2, z2) |
|
|
|
|||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
, b |
) x1x2 y1y2 z1z2; |
|
|
|
|
|
|||||||||||||||||||
a |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) |
| |
|
|
|
| x2 |
y2 |
z2 ; |
|
|
|
|
|
|
|
|
|||||||||||||
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
^ |
|
|
|
|
|
|
x x |
y y |
z z |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3) |
cos ( |
a |
, b) |
|
|
1 2 |
1 2 |
1 2 |
|
|
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x12 y12 z12 x22 y22 z22 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 y1y2 z1z2 0; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||
4) |
|
|
|
|||||||||||||||||||||||||
M1(x1, y1, z1), M2(x2, y2, z2) | M1M2| |
||||||||||||||||||||||||||||
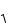
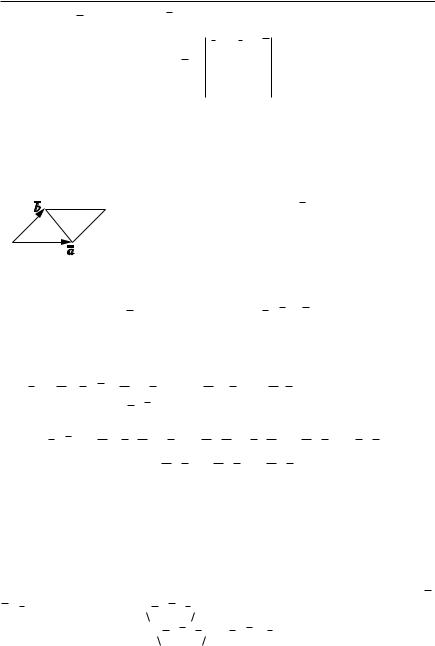
 (x2 x1)2 (y2 y1)2 (z2 z1)2 .
(x2 x1)2 (y2 y1)2 (z2 z1)2 .
Задача. Доказать, что диагонали четырехугольника с вершинами
A(1, 2, 3), B(7, 3, 2), C ( 3, 0, 6), D(9, , 4) перпендикулярны. |
||||||||
|
Решение. |
|
M62 |
|||||
|
|
|
|
|
|
|
|
|
|
AC ( 4, 2, 3), |
BD (2, 1, 2) (AC, BD) 8 2 6 0 AC BD. |
||||||
1.4. Векторное и смешанное произведение
Определение и свойства векторного произведения. Приложения век торного произведения. Определение и свойства смешанного произве дения. Приложения смешанного произведения.
1.4.1. Определение и свойства векторного произведения
ОПРЕДЕЛЕНИЕ 1. |
Векторным произведением векторов |
a |
, b на |
|||||||||||||||||||||||||
зывается вектор |
|
такой, что: |
||||||||||||||||||||||||||
c |
||||||||||||||||||||||||||||
1) |
| |
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
| |b |
| sin ( |
|
, b), |
|||||||||||||||||||
c |
a |
a |
||||||||||||||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||
c |
a |
c |
||||||||||||||||||||||||||
3) |
|
|
|
|
|
|
, |
|
образуют правую тройку, т. е. если смот |
|||||||||||||||||||
|
|
|
|
, b |
||||||||||||||||||||||||
a |
c |
|||||||||||||||||||||||||||
реть с конца вектора c, то кратчайший поворот от a к b происходит против часовой стрелки (pис. 1.8).
1.4. Векторное и смешанное произведение |
19 |
О б о з н а ч е н и е:
c [a, b] a ! b.
Свойства векторного произведения:
1) [a, b] 0 a, b — коллинеарные.
Доказательство:
^
[a, b] 0 sin (a, b) 0 a b a, b
— коллинеарные;
2) [a, b] [b, a] — вытекает из рис. 1.9; 3) примем без доказательства:
[a1 a2, b] [a1, b] [a2, b].
4) [ a, b] [a, b] [a, b] — доказать само стоятельно.
Вычисление векторного произведения в прямоугольной системе координат
Имеем очевидные равенства (pис. 1.10):
|
|
|
|
|
|
|
[k, j] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[ j, i] k, |
M62i, [i, k] j. |
|||||||||||||||||||||||
[i, i] 0, |
[ j, j] 0, |
[k, |
|
k] 0, |
||||||||||||||||||||
[i, j] k, |
[ j, k] i, |
[k, i] j, |
||||||||||||||||||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
a |
x1i y1 j z1k, |
b |
x2i y2 j z2 k, |
||||||||||||||||||
Рис. 1.9
Рис. 1.10
то, используя векторные произведения базисных векторов и свойст ва 3), 4), получим
[a1, b] [x1i y1 j z1k, x2i y2 j z2 k] x1x2[i, i] y1x2[j, i] z1x2[k, i]
x1y2[i, j] y1y2[j, j] z1y2[k, j] x1z2[i, k] y1z2[j, k] z1z2[k, k]
(y1z2 z1y2)i (z1x2 x1z2) j (x1y2 x2 y1)k
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 z1 |
|
x1 z1 |
|
|
|
x1 |
y1 |
|
i |
j |
k |
. |
||
|
|
|
|
|
|
x |
|
|
|
|
|||||
i |
j |
k |
y |
z |
|||||||||||
|
y2 z2 |
|
x2 z2 |
|
|
|
x2 |
y2 |
|
1 |
1 |
1 |
|
||
|
|
|
|
|
|
x2 |
y2 |
z2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
20 Глава 1. Элементы линейной алгебры и аналитической геометрии
Итак, если a (x1, y1, z1), b (x2, y2, z2), то
ij k
[ |
a |
, b] x1 |
y1 |
z1 . |
|
|
|
|||||||||||||||
|
|
x2 |
y2 |
z2 |
|
|
|
|||||||||||||||
1.4.2. Приложения векторного произведения |
||||||||||||||||||||||
1. Вычисление площадей параллелограмма и |
|
треугольника |
||||||||||||||||||||
(pис. 1.11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Sпар | |
|
|
|
|
|
| sin ( |
|
,^b |
)| |[ |
|
|
, |
|
|
|
|||||
|
|
|
| |b |
b |
]|, |
|||||||||||||||||
|
|
a |
a |
a |
||||||||||||||||||
|
|
Sтр |
1 |
Sпар |
1 |
|[ |
|
|
|
]|. |
|
|
|
|||||||||
|
|
|
, b |
|
|
|
||||||||||||||||
|
|
a |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
Рис. 1.11 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
aколлинеаренM62b [a, b] 0.
3.Векторное произведение позволяет по двум заданным векторам
указать вектор, им перпендикулярный.
Задача. Найти площадь параллелограмма, построенного на векто2. Векторное произведение позволяет проверить коллинеарность
^
рах a 2m n, b m 2n, если |m| | n| 1, (m, n) 30".
Решение. Sпар |[a, b]|. Используя свойства векторного произведе ния, получим
[a, b] [2m n, m 2n] 2[m, m] [n, m] 4[m, n] 2[n, n]
[m, n] 4[m, n] 3[m, n].
Поэтому
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
|
|
3 |
|
|
|
|
|
|
||||||||||||||||
Sпар |[a, b]| 3|[m, n]| 3|m| | n| sin (m, n) |
|
. |
|||||||||||||||||
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.4.3. Определение и свойства смешанного произведения
ОПРЕДЕЛЕНИЕ 2. Смешанным произведением трех векторов a, b, c называется число 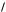 a, b, c
a, b, c , равное
, равное
 a, b, c
a, b, c ([a, b], c).
([a, b], c).
