
Основы высшей математики для инженеров 2009
.pdf
2.12. Формула Тейлора и ее приложения |
111 |
||||||||
ex 1 x |
x2 |
|
x3 |
|
xn |
|
xn 1 |
eA, |
|
|
|
|
|
|
|||||
2! 3! |
|
n! (n 1)! |
|
||||||
где 0 A xC Пусть | x | 1. Тогда при n 8 получим оценку остаточного
члена: |
n 1 |
|
|
|
||
3 |
3 |
3 |
|
|||
| R (x)| 3 |
x |
|
|
eA3 |
10 5. |
|
|
|
|
|
|||
n |
|
|
|
|
|
|
3(n 1)! |
3 |
9! |
||||
Поэтому, если взять первые 8 членов разложения ex при | x | 1, то мы получим число ex с точностью до 5 знаков после запятой.
Например,
e 1 1 1 1 1 1 1 1 1 . 2! 3! 4! 5! 6! 7! 8!
Проводя вычисления с 6 знаками после запятой, а затем округляя ре зультат, получим: e = 2,71828.
Можно показать, что lim |
xn 1 |
|
ex 0 для любых фиксирован |
|
|||
n (n 1)! |
|
||
ных x. Поэтому для любого x мы можем вычислить ex с любой степе нью точности, если взятьM62достаточно большое число членов.
2.12.3. Разложение функций по формуле Тейлора
Разложение функции sin x.
Для функций f (x) sin x и f (x) cos x путем последовательного дифференцирования можно вывести общее выражение для n2ой
производной: f (n)(x) f |
|
|
|
|
|
|
|
' |
Действительно, |
|
|
|
|
|
|
|
|||||||||
x |
n |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
f (x) sin x, |
|
|
|
|
|
|
|
|
|
|
|
|
f (0) 0, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(x) cos x sin |
|
|
|
|
' |
, |
|
|
|
|
|
f (0) 1, |
|
|
|
|
|
|
|
|||||
f |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
||||||
f |
(x) sin x sin |
x |
2 |
|
|
|
|
|
, |
|
f (0) 0, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
||||
f |
(x) cos x sin x 3 |
|
|
|
|
|
, |
f (0) 1, |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
. . . . . . . . . . . . . . . . . . . |
. . . . . . . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|||
f |
(n)(x) sin x n |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
f n(0) sin n |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
||||
f |
(n 1)(x) sin x |
(n 1) |
|
|
|
|
|
, |
|
|
f (n 1)(A) sin A |
(n 1) |
|
|
; |
||||||||||
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||

112 |
Глава 2. Дифференциальное исчисление функций одной переменной |
|
|
|||||||||||||||
|
sin x x |
x3 |
|
x5 |
|
x7 |
|
xn |
sin n |
' |
|
xn 1 |
sin |
7A (n 1) |
': |
, |
||
|
|
|
|
|
|
|
|
|
< |
|||||||||
|
3! |
5! |
7! |
|
n! |
2 |
|
(n 1)! |
|
9 |
2 |
|
||||||
|
|
|
|
8 |
; |
|
||||||||||||
где 0 |
A xC Очевидно, что sin |
7 |
A (n 1) |
': |
1 x. Можно показать, |
||||
|
|
|
|||||||
9 |
< |
||||||||
|
|
|
|
|
|
||||
|
|
|
|
8 |
|
2 ; |
|
||
что lim |
|
xn 1 |
|
|
|
|
|
||
|
|
0 при любом фиксированном x. Поэтому полученная |
|||||||
|
|
||||||||
n (n 1)! |
|
|
|
|
|
||||
формула позволяет для любого x вычислить sin x с любой степенью точности.
Вычислим, например, sin 20", ограничившись 2 членами разло
жения: |
|
|
|
|
|
|
|
'3 |
|
|
|
|
|
|
|
|
|
|
sin 20" = |
' |
|
|
|
= 0,342. |
|||
|
|
|
|
|
9 |
93 3! |
|||||||
Оценим ошибку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ' |
4 1 |
|
|
3 |
|
' |
4 |
1 |
|
||||
|
|
|
|
|
M62 |
|
= 0,00062 0,001. |
||||||
| R3| 3 |
|
|
|
|
sin (A |
')3 |
|
|
|
||||
3 9 |
|
4! |
|
|
3 |
|
9 |
|
4! |
||||
Таким образом, sin 20" 0,342 с точностью до 0,001.
Разложение функции y cos x.
f (x) cos x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
' |
|
|
|
|
|||||
f (x) sin x |
cos x |
|
|
, |
|
|
|||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
' |
|
|
||||
f (x) cos x cos x 2 |
|
|
|
|
|
, |
|||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
. . . . . . . . . . . . . . . . . . . |
|
||||||||||||||
|
|
|
|
' |
|
|
|
|
|
|
|
|
|||
f (n)(x) cos x n |
|
|
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
f (n 1)(x) cos |
7 |
|
(n 1) |
': |
, |
|
|
||||||||
9x |
|
|
< |
|
|
||||||||||
2 |
|
|
|
||||||||||||
|
|
8 |
|
|
|
|
|
; |
|
|
|
|
|||
cos x 1 |
x2 |
|
x4 |
|
xn |
||||||||||
|
|
n! |
|||||||||||||
2! |
4! |
|
|
|
|
|
|
|
|||||||
Вновь Rn(x) 0 при n 0.
f (0) 1,
f (0) 0,
f (0) 1,
. . . . . . .
f (n)(0) cos n ' ,
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
': |
|
||||
|
f (n 1)(A) cos 9A (n 1) |
|
|
< |
, |
||||||||
|
2 |
||||||||||||
|
|
|
|
|
|
8 |
|
; |
|
||||
cos n |
' |
|
xn 1 |
|
cos |
7 |
A (n 1) |
': |
. |
|
|||
|
|
|
|
|
|
|
|
|
|||||
2 |
(n 1)! |
9 |
|
< |
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
8 |
|
2 ; |
|
|
||||||
2.13. Исследование функций с помощью производных… |
113 |
2.13. Исследование функций с помощью производных. Возрастание и убывание функций. Исследование функций на экстремум
Условия возрастания и убывания функций. Точки экстремума. Необходимые условия экстремума. Достаточный признак экстремума. Достаточный при знак существования экстремума, основанный на знаке второй производной.
2.13.1. Условия возрастания и убывания функций
ОПРЕДЕЛЕНИЕ. Функция f (x) называется возрастающей (убы вающей) на [a, b] (на (a, b)), если для x2 x1 на этом отрезке (интер вале) имеет место неравенство f (x2) f (x1) ( f (x2) f (x1)).
Теорема. 1) если функция f (x) возрастает на отрезке [a, b] и диффе2
ренцируема на нем, то f (x) 0 для x [a, b]; |
|
|
|
|||||||
2) если f (x) непрерывна на [a, b] |
и дифференцируема на (a, |
b), |
и во |
|||||||
всех точках |
этого |
промежутка |
выполнено неравенство |
f (x) 0, |
то |
|||||
функция f (x) возрастает на [a, b]. |
|
2 |
|
|
|
|
||||
Поэтому |
|
M6-x |
|
при |
-x 0 |
|||||
Доказательство. |
1. Пусть |
f (x) |
возрастает. Тогда |
|||||||
f (x -x) f (x) и при -x 0 f (x -x) f (x). В обоих случаях |
|
|
||||||||
|
|
f (x -x) f (x) 0. |
|
|
|
|||||
|
|
f (x) lim |
|
f (x -x) f (x) |
0. |
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
-x 0 |
|
-x |
|
|
|
|||
2. Пусть |
f (x) 0 на (a, b). Выберем два любых значения x1 и x2 . |
|||||||||
По теореме |
Лагранжа f (x2) f (x1) f (c)(x2 x1) 0, так |
как |
f (c) 0. |
|||||||
Таким образом, f (x2) f (x1) f (x) возрастает на [a, b]. Аналогично доказывается следующая теорема.
Теорема 2. 1) если f (x) убывает на [a, b] и дифференцируема на нем, то f (x) 0;
2)если непрерывная на [a, b] функция f (x) дифференцируема на (a, b)
иf (x) 0, то f (x) убывает на [a, b].
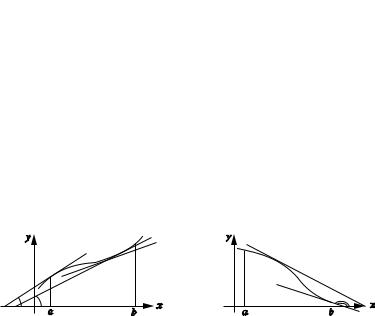
Геометрическая иллюстрация. |
Рис. 2.22 |
Рис. 2.23 |
114 Глава 2. Дифференциальное исчисление функций одной переменной
Если f (x) возрастает, то угол, составленный касательной с положи тельным направлением оси OX, — острый (в некоторых точках каса тельная может быть параллельна оси OX).
2.13.2. Точки экстремума. Необходимые условия экстремума
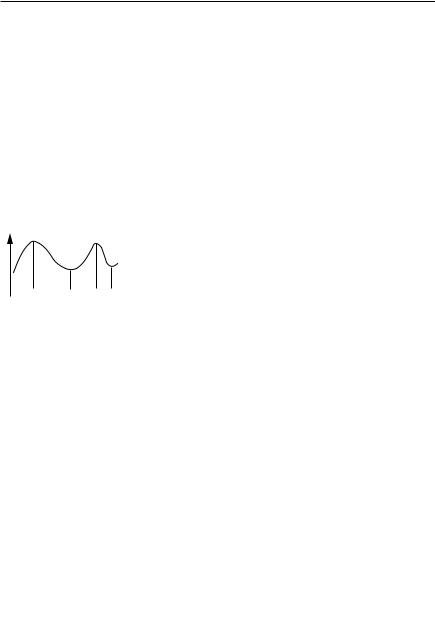
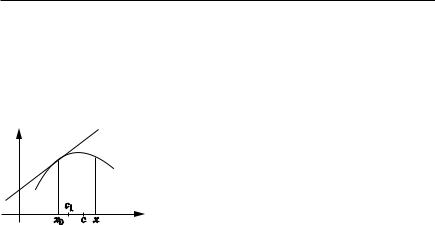
ОПРЕДЕЛЕНИЕ 1. Функция y f (x) имеет в точке x x1 локаль ный максимум, если существует такая окрестность точки x1, что f (x) f (x1) для любого x из этой окрестности.
ОПРЕДЕЛЕНИЕ 2. Функция f (x) имеет в точке x x2 минимум, если существует такая окрестность точки x2 , что f (x) f (x2) для всех точек x из этой окрестности.
x1, x3 — точки максимума, x2 , x4 — точки минимума.
Максимумы и минимумы — точки экстремума.
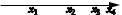 З а мM62е ч а н и я. 1. Функция, определенная на отрезке [a, b], может достигать max и min только внутри этого отрезка.
З а мM62е ч а н и я. 1. Функция, определенная на отрезке [a, b], может достигать max и min только внутри этого отрезка.
2. Если f (x) имеет max в точке x1, это не значит, что она в этой точке имеет наибольшее значение во всей области определения, а означает только, что ее значение в точке x1 больше значений во всех точках, доста точно близких к точке x1.
Необходимые условия экстремума.
Теорема. Если дифференцируемая в точке x1 функция имеет в этой точке max (или min), то f (x1) 0.
Доказательство. Пусть в точке x1 f (x) имеет max. Тогда, по опре делению, существует такая окрестность точки x1, что f (x) f (x1) для любого x из нее. Пусть -x достаточно мало, тогда f (x1 -x) f (x1) при -x любого знака.
При -x 0 |
|
f (x1 -x) f (x1) |
0. |
|
|
|
|
|
|
|
|||
|
|
|
-x |
|
|
|
При -x 0 |
|
f (x1 -x) f (x1) |
0. |
|
|
|
|
|
|
|
|||
|
|
|
-x |
|
|
|
Следовательно, |
|
lim |
f (x1 -x) f (x1) |
f (x ) 0 |
f (x ) 0. |
|
|
|
|||||
|
-x 0 |
-x |
1 |
1 |
||
|
|
|
||||
Аналогично доказывается утверждение для минимума.

2.13. Исследование функций с помощью производных… |
115 |
||||||||
Однако f (x) может иметь экстремум и в тех |
|
|
|||||||
точках, где она не дифференцируема. |
|
|
|||||||
|
|
||||||||
y 1 3 |
|
, y |
2 |
|
|
. |
|
|
|
x2 |
|
|
|||||||
3 |
|
|
|
|
|||||
|
|
|
|||||||
|
|
|
3 x |
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
При x 0 — max, но f (x) в этой точке не сущест вует (рис. 2.25).
Итак, если функция y f (x) в некоторой точке x имеет экстремум, то производная f (x) в этой точке равна 0 или не существует.
Точки, в которых производная равна нулю или не существует, на зываются критическими точками первого рода.
З а м е ч а н и е. Равенство производной нулю есть только необходимое условие экстремума, но не достаточное. Например, для функции y x3 в
точке 0, y 3x2 обращается в 0, но ясно, что эта функция не имеет экс тремума в точке 0.
2.13.3. ДостаточныйM62признак экстремума
Теорема 1. Если непрерывная функция y f (x) имеет производную во всех точках некоторого интервала, содержащего критическую точку (за исключением, может быть, самой точки) и если при переходе аргумента через эту точку слева направо производная f (x) меняет знак с (–) на (+), то это точка минимума, если с (+) на (–) — точка максимума.
Доказательство. Пусть для определенности производная меняет знак с (+) на (–). Тогда слева от x x0 производная положительна, а справа — отрицательна. Следовательно, существует такое число h 0, что на [x0 h, x0] возрастает, а на [x0, x0 h] убывает. Поэтому значе ния функции в точке x0 больше, чем ее значения во всех остальных точках отрезка [x0 h, x0 h], а это и означает, что в точке x x0 f (x) имеет максимум.
Аналогично доказательство для случая минимума.
З а м е ч а н и е. Если при переходе через точку x0 производная не меня ет знака, то в этой точке функция не имеет ни минимума, ни максимума.
П р и м е р. Исследовать на экстремум функцию y x2 2 x 2. x 1

116 Глава 2. Дифференциальное исчисление функций одной переменной
2.13.4. Достаточный признак существования экстремума, основанный на знаке 2>й производной
Теорема 2. Пусть в точке x x0 первая производная функции обра2 щается в нуль. Если в этой точке существует и отлична от 0 вторая производная f (x0), то в точке x x0 функция f (x) имеет max, если f (x0) 0, и min, если f (x0) 0.
Доказательство. Пусть f (x0) 0, f (x0) 0. |
Тогда, по определе |
||||||
нию, |
|
|
|
|
|
|
|
f (x ) lim |
f (x0 -x) f (x0) |
lim |
f (x0 -x) |
. |
|||
|
|
|
|
||||
0 |
|
-x |
|
-x 0 |
-x |
||
-x 0 |
|
|
|||||
|
|
f (x0 -x) |
|
|
|
|
|
Так как f (x0) 0, то и |
|
|
0 при достаточно малых -x. При |
||||
|
|
||||||
|
|
-x |
|
|
|
|
|
-x 0 f (x0 -x) 0, а при -x 0 |
f (x0 -x) 0. Следовательно, при |
||||||
переходе через x x0 f (x) меняет знак с (+) на (–). Следовательно, |
|||||||
по теореме 1 f (x) имеет максимум в точке x x0. |
|||||||
З а м е ч а н и е. Если f (x0) 0 и |
f (x0) 0, то ничего сказать нельзя. |
||||||
В этом случае приходитсяM62обращаться к первому достаточному признаку.
2.14. Наибольшее и наименьшее значение функции на отрезке. Выпуклость, вогнутость. Точки перегиба
Наибольшее и наименьшее значение функции на отрезке. Выпуклость и вогнутость функции. Точки перегиба. Необходимое условие существо вания точек перегиба. Достаточное условие.
2.14.1. Наибольшее и наименьшее значение функции на отрезке
Пусть функция f (x) непрерывна на отрезке [a, b]. Тогда эта функ ция достигает своего наибольшего и наименьшего значения на [a, b]. Очевидно, она может достигать наибольшего и наименьшего значения либо в точках экстремума, либо на концах отрезка [a, b]. Отсюда полу чаем правило отыскания наибольшего и наименьшего значений.
1.Отыскиваем критические точки f (x) на (a, b).
2.Вычисляем значения f (x) на концах [a, b] и в критических точках.
3.Выбираем из всех значений наибольшее и наименьшее.
2.14. Наибольшее и наименьшее значение функции на отрезке… |
117 |
Задача. Открытый жестяной бак с квадратным основанием должен вмещать V литров. При каких размерах бака на его изготовление по требуется наименьшее количество жести?
Решение. Пусть x — сторона основания бака ( x 0). Тогда V — x2
высота бака. Поверхность бака
S x2 |
4x |
V |
x2 |
4V |
; |
x2 |
x |
S 2 x 4V ; S 0 x 3 2V ; x2
|
|
8V |
0 при |
x 3 |
|
. |
|
S 2 |
|
2V |
|||||
3 |
|||||||
|
|
x |
|
|
|
|
Следовательно, в точке x 3 2V S имеет наименьшее значение. Най дем отношение высоты бака Н к стороне основания:
2V S имеет наименьшее значение. Най дем отношение высоты бака Н к стороне основания:
Н |
V |
: |
Н |
|
V |
|
V |
|
1 |
. |
x2 |
|
|
|
|
||||||
|
|
х x3 |
|
2V 2 |
||||||
2.14.2. ВыпуклостьM62и вогнутость графика функции
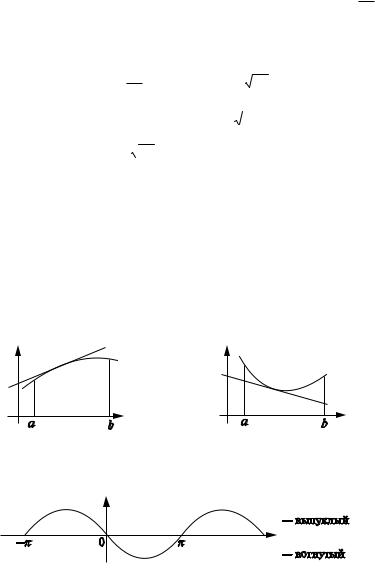
График дифференцируемой на (a, b) функции называется выпук лым на (a, b), если он расположен ниже любой своей касательной на этом интервале (рис. 2.26), и вогнутым, если он расположен выше лю бой своей касательной (рис. 2.27).
Рис. 2.26 |
Рис. 2.27 |
График одной и той же функции в одних интервалах может быть выпуклым, а в других — вогнутым (рис. 2.28).
Рис. 2.28
118 Глава 2. Дифференциальное исчисление функций одной переменной
Теорема 1. Пусть функция y f (x) имеет вторую производную f (x) во всех точках (a, b). Тогда если f (x) 0 x (a, b), то график функции вогнут, а если f (x) 0, то график выпуклый.
Доказательство. Пусть f (x) 0. Докажем, что график функции f (x) выпуклый. Пусть x0 — произвольная точка (a, b). Напишем урав нение касательной к графику функции:
y f (x0) f (x0)(x x0) y f (x0) f (x0)(x x0).
Найдем разность абсцисс графика функции и касательной в произвольной точке x.
Y y f (x0) f (x) f (x0)(x x0).
По теореме Лагранжа f (x0) f (x) f (x)(x0 x), поэтому
Y y f (x)(x0 x) f (x0)(x x0) (x x0)[f (x0) f (x)],
где x0 c1 |
c и |
M62 |
|
где c заключено между x0 |
и x. Разность f |
(x0) f (x) вновь преобразуем |
|
по формуле Лагранжа: |
|
|
|
|
f (x0) f (c) f (c1)(x0 c), |
||
|
Y y f (c1)(x x0)(x0 c). |
||
Очевидно, |
x x0 и |
x0 c имеют |
разные знаки, поэтому |
(x x0)(x0 c) 0, f (c1) 0 по условию. Следовательно,
Y y 0 Y y.
Таким образом, ордината касательной больше ординаты графика в любой точке x. По определению график функции является выпуклым на (a, b).
Аналогично доказывается теорема для случая f (x) 0.
2.14.3. Точки перегиба. Необходимое условие существования точек перегиба. Достаточное условие
ОПРЕДЕЛЕНИЕ. Точка графика функции, отделяющая его вы пуклую часть от вогнутой, называется точкой перегиба.
Теорема 2 (необходимое условие существования точки перегиба).
Если x x0 — точка перегиба графика функции, то f (x0) 0.

2.15. Асимптоты. План исследования функций и построения графиков 119
Доказательство. В предположении противного f (x0) 0. Пусть на пример, f (x0) 0; в некоторой окрестности точки f (x0) 0, но тогда по теореме 1 график f (x) вогнут в этой окрестности. Последнее проти воречит предположению о том, что x0 — абсцисса точки перегиба.
Теорема 3 (достаточное условие существования точки перегиба).
Если вторая производная f (x) непрерывной функции меняет знак при пе2 реходе через точку x x0, то точка с абсциссой x x0 — точка перегиба графика функции.
Доказательство. Пусть f (x0) 0 при x x0 и f (x0) 0 при x x0, тогда слева от x0 график выпуклый, а справа — вогнутый. Следова тельно, точка с координатами (x0, f (x0)) — точка перегиба.
Так же, как и в случае исследования на экстремум, перегиб может быть и в тех точках, где вторая производная не существует.
Таким образом, точки перегиба (их абсциссы) нужно искать среди тех точек, в которых производная y f (x) равна нулю или не сущест вует. Такие точки называются критическими точками второго рода.
2.15. Асимптоты. План исследования функций и построения графиков
M62
Асимптоты графика функции. Общая схема исследования функции и по строения ее графика. Дифференциал длины дуги.
2.15.1. Асимптоты графика функции
Рассмотрим графики функций, ветви которых удаляются в беско нечность в вертикальном, наклонном или в горизонтальном направле нии. Характерным для многих таких функций является то, что точки графика при удалении на бесконечность асимптотически (неограни ченно) приближаются к некоторым прямолинейным границам, кото рые называются асимптотами.
Асимптотой графика функции называется прямая линия, обладаю щая тем свойством, что расстояние от переменной точки на графике функции до этой прямой стремится к 0 при неограниченном удалении точки в бесконечность.
Вертикальные асимптоты. Пусть при x x0 0 функция неограни
ченно возрастает по абсолютной величине, т. е. пусть lim |
| f (x)| |
x x0 0 |
является |
или lim | f (x)| . Тогда прямая x x0 по определению |
|
x x0 0 |
|
асимптотой.
120 |
Глава 2. Дифференциальное исчисление функций одной переменной |
|
||||||||||
Итак, для отыскания вертикальной асимптоты графика функции |
||||||||||||
y f (x) нужно найти такую точку x0, в которой f (x) терпит бесконеч |
||||||||||||
ный разрыв. Тогда x x0 |
— вертикальная асимптота. |
|
|
|
||||||||
П р и м е р 1. f (x) x2 1 . |
|
|
|
|
|
|
|
|
||||
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) ; |
|
|
|
|
|
|
|
|
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) . |
|
|
|
|
|
|
||
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
Таким образом, вертикальная прямая с уравнением x 2 — верти |
||||||||||||
кальная асимптота. |
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
П р и м е р 2. y ex 1. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
lim |
ex 1 «e » 0, |
|
|
|
|
|
||||
|
|
x 1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
lim |
ex 1 «e » . |
|
|
|
|
|
|||
|
|
x 1 0 |
|
|
|
|
|
|
|
|
|
|
Здесь x 1 — вертикальная асимптота. |
|
|
|
имеет |
наклонную |
|||||||
Наклонные |
|
Пусть |
кривая |
|
|
f (x) |
||||||
асимптоты.M62y |
|
|
|
|
|
|||||||
асимптоту y kx b. Найдем k и b. |
|
|
|
|
|
|
|
|||||
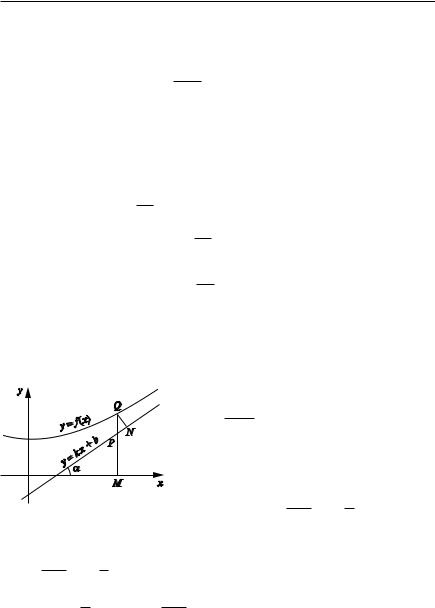
|
|
|
|
Рассмотрим случай, когда x . По |
||||||||
|
|
|
определению асимптоты NQ 0. Поэто |
|||||||||
|
|
|
му PQ NQ . |
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
cos) |
|
|
|
|
|
|
|
|
|
|
|
Но PQ f (x) kx b. |
|
|
|
|
||||
|
|
|
|
|
lim [f (x) kx b] |
|
|
|
||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x |
7 f (x) k b : 0. |
|
||||
|
Рис. 2.30 |
|
|
x |
|
9 |
x |
|
< |
|
|
|
|
|
|
|
8 |
|
x; |
|
|
||||
Так |
как |
первый |
сомножитель |
стремится |
к |
, |
то |
|||||
lim 7 f (x) k b : 0. |
|
|
|
|
|
|
|
|
|
|
||
9 |
x |
< |
|
|
|
|
|
|
|
|
|
|
x 8 |
x; |
|
|
|
|
|
|
|
|
|
|
|
Но |
lim b 0 lim |
f (x) k. Зная k, можем найти b из равенства |
||||||||||
|
x x |
x |
x |
|
|
|
|
|
|
|
|
|
0 lim (f (x) kx b), т. е. b lim [f (x) kx].
x |
x |
