Основы высшей математики для инженеров 2009

нельзя было бы перейти к пределу. Точка P0 называется точкой непре рывности функции f (P).

Если в некоторой точке P0(x0, y0) не выполняется условие (1), то P0(x0, y0) — точка разрыва функции. Например:

1)z f (x, y) определена во всех точках некоторой окрестности P0(x0, y0), за исключением точки P0;

2)z f (x, y) определена во всех точках окрестности точки P0, но

не существует предела f (x, y) при x x0, y y0.

202 Глава 4. Дифференциальное исчисление функций многих переменных

Рассматривая разности x x0, y y0 как приращения -x, -y неза висимых переменных, а разность f (x, y) f (x0, y0) как приращение функции, можно сказать, что функция непрерывна, если бесконечно малым приращениям аргумента отвечает бесконечно малое прираще ние функции.

Определенная выше непрерывность функции в точке есть непре рывность по совокупности переменных. Если она имеет место, то

4.2. Частные производные. Дифференциал

Свойства непрерывных в замкнутой и ограниченной области функций. Частные производные 1 го порядка. Геометрический смысл частных производных функции двух переменных. Полное приращение функции и полный дифференциал.

4.2.1.СвойстваM62непрерывных в замкнутой

иограниченной области функций

Функция z f (x, y), непрерывная в замкнутой ограниченной об ласти G, обладает следующими свойствами.

1. В области G найдется по крайней мере одна точка N0(x0, y0) та кая, что для всех других точек области справедливо неравенство

f (x0, y0) f (x, y),

и по крайней мере одна точка N1(x1, y1) такая, что

f (x1, y1) f (x, y)

для всех других точек области.

Значение f (x0, y0) M — наибольшее значение функции в облас ти G, значение f (x1, y1) m — наименьшее значение функции в этой области.

Таким образом, непрерывная функция в замкнутой ограниченной области G достигает по крайней мере один раз своего наибольшего значения М и наименьшего значения m.

2. Если М и m — наибольшее и наименьшее значения функции

f (x, y) в области G, то для : M m найдется в области такая точка N *(x*, y*), что f (x*, y*) .

Следствие. Если f (x, y) непрерывна в замкнутой ограниченной об ласти и принимает в ней как положительные, так и отрицательные значения, то внутри области найдутся точки, в которых f (x, y) 0.

4.2.2. Частные производные первого порядка

Пусть задана функция z f (x, y). Пусть y y0, а x0 получает при ращение -x. Тогда функция получит приращение, которое назовем ча стным приращением по переменной x и обозначим -xz:

-xz f (x0 -x, y0) f (x0, y0).

ОПРЕДЕЛЕНИЕ. Частной производной 1 го порядка функции z f (x, y) в точке (x0, y0) по переменной x называется предел отноше ния частного приращения функции в этой точке к вызвавшему его

M62

приращению аргумента при стремлении последнего к 0:

fx(x0, y0) lim -xz .

-x 0 -x

Аналогично вводятся понятия частного приращения и частной производной функции z f (x, y) по переменной y:

- yz f (x0, y0 -y) f (x0, y0),

fy(x0, y0) lim - yz .

-y 0 -y

Так как производные зависят от точки P(x, y), то их можно рас сматривать как функции двух переменных. Для частных производных

Аналогично вводятся понятия частных производных для функций большего числа переменных.

204 Глава 4. Дифференциальное исчисление функций многих переменных

Из определения частной производной следует, что правила и фор мулы дифференцирования, выведенные для производных функции одной переменной, сохраняются для частных производных функций нескольких переменных.

П р и м е р. f (x, y) x2 y 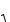x2 y2 .

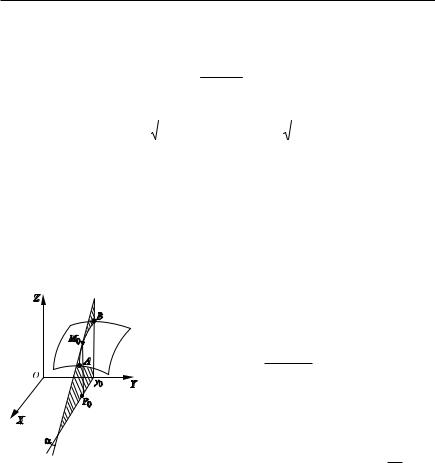
Рассмотрим точку P0(x0, y0) в плоскости XOY и соответствующую ей точку M0(x0, y0, z0) на поверхности. Рассмотрим плоскую кривую

4.2.4. Полное приращение функции и полный дифференциал

Рассмотрим функцию z f (x, y). Пусть независимые переменные получили приращения -x, -y. Тогда приращение функции имеет вид

-z f (x -x, y -y) f (x, y).

Геометрически полное приращение функции f (x, y) определяет приращение координаты z при переходе из точки P(x, y) в точку

P1(x -x, y -y).

Например, для функции z xy

-z (x -x)(y -y) xy xy у-x x-y -x-y xyу-x x-y -x-y.

Заметим, что -x-y стремится к 0 быстрее, чем первые два слагаемых.

ОПРЕДЕЛЕНИЕ. Функция z f (x, y) называется дифференцируе мой в точке P(x, y), если ее полное приращение можно предста вить в виде

-z A-x B-y I(-x, -y),

где I(-x, -y) — бесконечно малая более высокого порядка, чем

+ -x2 -y2 ; А, В — постоянные (не зависящие от -x, -y). Главная часть приращения, линейная относительно -x, -y, назы

Доказательство. По определению

-z A-x B-y I(-x, -y)

для любых -x, -y. Пусть -y 0, -x 0, тогда -z -xz и -xz A-x I. Поэтому

206 Глава 4. Дифференциальное исчисление функций многих переменных

Таким образом, если функция z f (x, y) дифференцируема в точ ке, то ее полный дифференциал имеет вид

dz Hz -x Hz -y.

Hx Hy

Обратное утверждение, вообще говоря, неверно, однако имеет ме сто следующая теорема.

Теорема. Если частные производные Hz и Hz непрерывны в некоторой

Hx Hy

окрестности точки P(x, y), то функция z f (x, y) дифференцируема

в точке P(x, y).

Приращения независимых переменных называют их дифферен циалами и обозначают dx, dy; тогда

4.3. Применение полного дифференциала к приближенным вычислениям. Производные сложных и неявных функций

Приложение полного дифференциала к приближенным вычислениям. Дифференцирование сложных функций. Неявные функции и их диффе ренцирование.

4.3.1. Приложение полного дифференциала к приближенным вычислениям

Полным дифференциалом функции нескольких переменных мож но воспользоваться для приближенных вычислений. Пусть дана диф ференцируемая функция z f (x, y). Ее полное приращение выражает ся формулой

-z fx(x, y)-x fy(x, y)-y I(-x, -y).

4.3. Применение полного дифференциала к приближенным вычислениям... 207

Здесь I(-x, -y) стремится к нулю быстрее, чем + -x2 -y2 . По

этому при малых +, т. е. при малых | -x | и | -y |, слагаемым I(-x, -y) можно пренебречь и писать

т. е. приращение функции можно заменить ее полным дифференциа лом. Так как z f (x, y), то

Формулой (2) можно пользоваться для приближенных вычислений значений функции двух переменных в точке (x -x, y -y), если извест ны значения функции и ее частных производных в самой точке (x, y).

4.3.2. Дифференцирование сложных функций

Пусть дана функция двух переменных z f (x, y), причем аргумен ты этой функции являются функциями одной переменной t: x x(t), y y(t). Тогда z есть сложная функция одной независимой перемен

ной t. Поставим задачу найти производную этой сложной функции dz ,

208 Глава 4. Дифференциальное исчисление функций многих переменных

решении этой задачи будем предполагать, что функции x x(t) и y y(t) имеют производные в точке t, а функция z f (x, y) в соответст вующей точке (x, y) дифференцируема.

Пусть независимая переменная t получает приращение -t; тогда пе ременные x и y получат соответственно приращения -x и -y, а функция z — приращение -z. Так как функция z по предположению дифферен цируема, то ее полное приращение -z может быть представлено в виде

причем lim I 0, где + -x2 -y2 . Разделив обе части равенства (3)

+ 0 +

на -t и переходя к пределу при -t 0, получим

Если каждый из пределов, стоящих в правой части этого равенст ва, существует, то существует и предел, стоящий в левой части этого

Прежде чем находить lim I, отметим, что при -t 0 также и + 0.

-t 0 +

Но тогда lim I lim I 0 и, следовательно,

dz y x y 1 cost x у ln x 2t t2(sin t)t2 1 cost (sin t)t2 ln (sin t) 2t. dt

Рассмотрим теперь функцию z f (x, y) при условии, что y y(x). Здесь переменная z есть функция одной переменной x: z f (x, y(x)). Этот случай сводится к предыдущему, причем роль переменной t игра ет x. По формуле (5) имеем

Формула (6) носит название формулы полной производной.

П р и м е р. z arcsin xy, y ln x.

Предположим теперь, что z f (x, y), причем x x(u, v) и y y(u, v). Тогда z есть сложная функция двух независимых переменных u и v.

Пользуясь формулой (5), можем найти частные производные Hz и Hz

Hu Hv

этой сложной функции:

Hz Hz Hx Hz Hy ;

Hu Hx Hu Hy Hu

Hz Hz Hx Hz Hy .

Hv Hx Hv Hy Hv

210 Глава 4. Дифференциальное исчисление функций многих переменных

П р и м е р. z arctg x , x u sin v, y u cos v.

принадлежащему некоторому множеству М, соответствует единствен ное значение y, которое совместно с x удовлетворяет уравнению (7), то говорят, что это уравнение определяет на множестве М неявную

Таким образом, для неявной функции y ((x), определенной урав нением (7), имеет место тождество F[x, ((x)] J 0.

Не следует однако думать, что всякую неявную функцию можно представить в виде явной элементарной функции. Например, урав

нение

2 y 2 y x2 1 0

задает неявную функцию y, так как существуют пары значений x и y, удовлетворяющие данному уравнению. Но это уравнение нельзя раз решить относительно y так, чтобы y выражался через элементарные функции от аргумента x.

Теорема существования неявной функции. Если функция F(x, y) и

ее частные производные Fx(x, y) и Fy(x, y) определены и непрерывны в некоторой окрестности точки P0(x0, y0), и при этом F(x0, y0) 0, а

Fy(x0, y0) 0, то уравнение F(x, y) 0 определяет в некоторой окрест2 ности точки P0(x0, y0) единственную неявную функцию y y(x), непре2

рывную и дифференцируемую в некотором интервале, содержащем точку x0, причем y(x0) y0.