
Основы высшей математики для инженеров 2009
.pdf
4.6. Наибольшее и наименьшее значения функции двух переменных… |
221 |
x y 3. Здесь y 3 x и функция z f (x, y) принимает вид z x2 (3 x)2 (3 x)x x 3 x 3x2 9x 6.
z 6x 9 0 x 3 y 3 3 3 ;
|
|
|
2 |
|
|
2 |
2 |
||
|
3 |
3 |
|
3 |
|
|
|||
z |
|
, |
|
|
|
, |
|
||
|
|
4 |
|
||||||
|
2 |
2 |
|
|
|
||||
|
z(0, 3) |
6, |
|
|
|
||||
|
z( 3, 0) |
6. |
|
|
|
||||
Итак, окончательно, наибольшее значение функция z f (x, y) прини мает в точке (0, –3) и в точке (–3, 0): z 6. Наименьшее значение функция z принимает в точке ( 1, 1):
z 1.
4.6.3. Условный экстремум. Уравнение связи
Рассмотрим следующуюM62задачу: из данного куска жести площадью 2a надо сделать закрытую коробку в форме параллелепипеда, имеющую наибольший объем.
Пусть дана ширина, высота коробки соответственно x, y, z. Задача сводится к нахождению максимума функции
v xyz
при условии, что
2 xy 2 xz 2 yz 2a.
Это задача на условный экстремум: переменные x, y, z связаны ус ловием 2 xy 2 xz 2 yz 2a (уравнением связи).
Пусть требуется найти экстремумы функции
z f (x, y) |
(1) |
при условии |
(2) |
((x, y) 0. |
Так как есть уравнение связи (2), то из двух переменных x и y незави симым будет только одна (например x), т. к. y определяется из уравне ния (2) как функция от x. Если уравнение (2) можно разрешить, то, подставляя в равенство (1) y y(x), мы получим функцию одной пере менной x, которая легко исследуется на экстремум.
Но можно и не разрешать уравнение (2) относительно y.

222 Глава 4. Дифференциальное исчисление функций многих переменных
4.6.4. Необходимые условия условного экстремума
Ясно, что при тех значениях x, при которых функция f (x, y) имеет экстремум, ее производная dz равна 0. Найдем dz из уравнения (1),
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
||
помня, что y есть функция от x: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dz |
|
Hf |
|
Hf |
|
dy |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dx |
|
Hx |
|
|
|
|
Hy dx |
|
|||||||||||
Следовательно, в точках экстремума |
|
|||||||||||||||||||
|
|
Hf |
|
|
Hf |
|
dy |
0. |
(3) |
|||||||||||
|
|
Hx |
Hy |
|
|
|||||||||||||||
|
|
|
|
|
|
|
dx |
|
||||||||||||
Из равенства (2) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
H( |
|
H( |
|
dy |
0. |
(4) |
||||||||||||
|
|
Hx |
|
|
||||||||||||||||
|
|
|
|
|
Hy dx |
|
||||||||||||||
Умножим члены равенства (4) на некоторый коэффициент и сложим
с членами равенства (3): |
|
|
|
|
|
|
|
|
|
|
|
|
0. |
(5) |
||||||
|
f |
|
M6f 2dy |
|||||||||||||||||
Hf |
|
|
Hf dy |
|
H( |
|
H( dy |
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Hx |
|
|
Hy dx |
|
|
Hx Hy dx |
|
|
||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H |
|
|
|
|
H( |
H |
|
|
H( |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Hx |
|
Hx Hy |
Hy dx |
|
|
|
||||||||||||||
Последнее равенство выполнено во всех точках экстремума. Подбе рем так, чтобы для всех x, y, при которых функция z f (x, y) имеет экстремум, вторая скобка в равенстве (5) обратилась в 0:
|
Hf |
|
H( |
0. |
||
|
Hy |
|
||||
|
|
Hy |
||||
(Для определенности предположим, что в критических точках |
H( |
не |
||||
|
||||||
равна 0.) Но тогда |
|
|
|
Hy |
||
|
|
|
|
|
||
|
Hf |
|
H( |
0. |
||
|
Hx |
|
||||
|
|
Hx |
||||
Таким образом, в точках экстремума удовлетворяются три уравнения:
Hf |
|
H( |
0, |
|
|
|
|
|
|
||
&Hx |
|
|
|||
|
Hx |
|
|||
& |
|
|
|
|
|
& |
|
|
|
|
|
Hf |
|
H( |
0, |
(6) |
|
|
|
|
|
||
&Hy |
|
|
|||
|
Hy |
|
|||
&
&((x, y) 0

4.7. Достаточные условия существования условного экстремума… |
223 |
с тремя неизвестными x, y, . Из этих уравнений определяем x, y и , которое играло только вспомогательную роль и в дальнейшем нам не требуется.
Из вывода следует, что система (6) дает лишь необходимые усло вия существования экстремума.
Заметим, что левые части уравнений (6) — это частные производ
ные функции
F(x, y, ) f (x, y) ((x, y) по переменным x, y, .
Функция F(x, y, ) называется функцией Лагранжа, а число —
множителем Лагранжа.
4.7. Достаточные условия существования условного экстремума. Метод наименьших квадратов
Достаточные условия существования условного экстремума. Пример решения задачи на отыскание условного экстремума. Метод наимень ших квадратов. M62
4.7.1. Достаточные условия существования условного экстремумa
Итак, для отыскания точек, в которых возможен условный экстре мум, необходимо составить функцию Лагранжа и найти критические точки для этой функции. Вопрос о существовании и характере услов ного экстремума решается с помощью достаточного признака для функции Лагранжа. Таким образом, чтобы найти условный экстре мум, нужно найти обычный экстремум для функции Лагранжа, ис пользуя при этом уравнение связи ((x, y) 0.
З а м е ч а н и е. Иногда удобно при проверке достаточных условий экс тремума пользоваться критерием, основанным на знаке второго дифферен циала функции Лагранжа. Этот критерий формулируется следующим обра зом: пусть в критической точке d2F 0, тогда эта точка условного миниму ма. Если d2F 0, то имеем точку условного максимума. Здесь
d2F |
|
H2F |
(dx)2 |
|
02F |
H2F |
(dy)2, |
|
|
|
2 |
|
dx dy |
|
|||
Hx2 |
Hx Hy |
Hy 2 |
||||||
где дифференциалы dx и dy связаны соотношением
H( dx H( dy 0.
Hx Hy

224 Глава 4. Дифференциальное исчисление функций многих переменных
Рассмотренный метод распространяется на исследование условно го экстремума функции любого числа переменных при наличии одно го или нескольких уравнений связи. Здесь приходится вводить в функ цию Лагранжа столько неопределенных множителей, сколько имеется уравнений связи.
4.7.2. Пример решения задачи на отыскание условного экстремума
Найти экстремум функции z 6 4x 3y при условии, что x2 y2 1. Решение. Геометрически задача сводится к нахождению наиболь шего и наименьшего значения координаты z плоскости z 6 4x 3y
в точках ее пересечения с цилиндром x2 y2 1. Составим функцию Лагранжа
F(x, y, ) 6 4x 3y (x2 y2 1).
Вычислим производные этой функции по переменным x, y и :
MHF 624 2 x,
Hx
HF 3 y,
Hy
HF x2 y2 1.
H
Приравняв эти производные к нулю, получим систему уравнений для отыскания координат критической точки
4 2 x 0,
&
3 2 y 0, &x2 y2 1 0.
Решив эту систему, получим координаты двух критических точек
x |
|
4 |
, |
y |
|
3 |
, |
5 |
; |
x |
|
4 |
, |
y |
|
3 |
, |
5 |
. |
|
|
|
|
|
|
||||||||||||||
1 |
5 |
|
1 |
|
5 |
1 |
2 |
|
2 |
5 |
|
2 |
|
5 |
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Проверим достаточные условия экстремума:
A |
H2 F |
2 , |
B |
H2 F |
0, |
C |
H2 F |
2 . |
Hx2 |
|
Hy2 |
||||||
|
|
|
HxHy |
|
|
|||

4.7. Достаточные условия существования условного экстремума… 225 |
||||||||||||
Для первой точки |
|
|
|
|
|
|
|
|
|
|
|
|
AC B2 4 2 0, |
|
|
A 2 5 0. |
|||||||||
|
|
|
|
|
|
4 |
|
|
|
3 |
||
Таким образом, точка с координатами |
|
|
|
, |
|
|
является точкой услов |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
5 |
|
|
|
5 |
||
ного минимума функции z 6 4x 3y. |
|
|
|
|
|
|
|
|||||
Для второй точки |
|
|
|
|
|
|
|
|
|
|
|
|
AC B2 4 2 0, |
|
A 2 5 0. |
||||||||||
Т. е. точка с координатами x |
|
4 |
|
, y |
|
3 |
является точкой условного |
|||||
|
|
|||||||||||
2 |
5 |
|
2 |
|
|
|
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
максимума рассматриваемой функции.
4.7.3. Метод наименьших квадратов
Метод наименьших квадратов широко используется при обработке экспериментальных данныхM62в тех случаях, когда теория дает закон, оп ределяющий уравнение связи между физическими величинами, но с некоторыми неопределенными параметрами (коэффициентами), для определения которых проводятся эксперименты. Например, удлине ние -l линейного образца с начальной длиной l0 и начальной темпера турой T0 прямо пропорционально приращению его температуры Т:
-l )l0(T T0)
где ) — коэффициент линейного расширения, который определяется экспериментально.
В соответствии с законом Гука имеет место линейная связь между напряжениями и деформациями упругого деформируемого тела. В об щем случае линейной связи двух физических величин х, у дается соот ношение
Y(x) ax b,
с двумя параметрами a, b, для определения которых проводятся экспе рименты и для заданной последовательности x1, x2, …, xn определяют ся соответствующие им значения y1, y2, …, yn. Полученные результаты записываются в таблицу
x |
x1 |
x2 |
x3 |
… |
xn |
y |
y1 |
y2 |
y3 |
… |
yn |
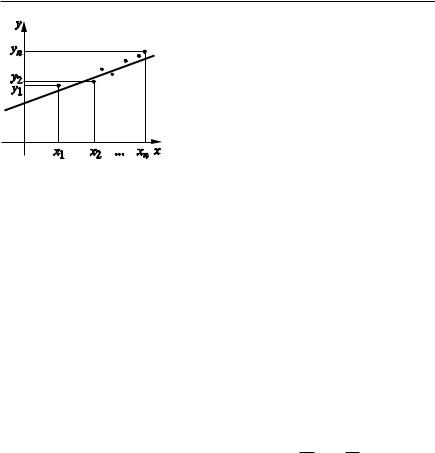

4.7. Достаточные условия существования условного экстремума… |
227 |
|||
|
n |
n |
n |
|
&aFxi2 bFxi Fxi yi, |
|
|||
& |
i 1 |
i 1 |
i 1 |
|
|
n |
n |
|
|
&&aFxi bn Fyi. |
(3) |
|||
|
i 1 |
i 1 |
|
|
Легко проверить, что определитель системы (3) отличен от 0, по этому такая система имеет единственное решение.
Покажем, что для найденных значений a и b функция f (a, b) имеет минимум:
2 |
n |
2 |
f |
|
|
2 |
n |
||||
A |
H f |
2Fxi2; |
C |
H |
2n; |
B |
H f |
2Fxi. |
|||
Ha2 |
Hb2 |
HaHb |
|||||||||
|
i 1 |
|
|
|
i 1 |
||||||
|
|
|
|
2 |
|
|
|||||
|
|
n |
n |
|
|
|
|||||
- AC B2 4nFxi2 |
4 Fxi 4F(xi x j)2 0, A 0. |
||||||||||
|
|
i 1 |
i 1 |
i, j |
|
|
|
||||
i j
Таким образом, согласно достаточному условию существования экс тремума, функция f (a, b) M62имеет минимум.
Подставляя найденные значения a и b в равенство (1), получим линейную функцию, наилучшим образом отражающую зависимость между величинами x и y, найденными экспериментально.
П р и м е р. Пусть на основании эксперимента получены четыре значения искомой линейной функции y при четырех значениях аргу мента, которые записаны в таблице.
|
x |
|
1 |
2 |
3 |
5 |
|
|
y |
|
3 |
4 |
2,5 |
0,5 |
|
Составляем выражение f (a, b): |
|
|
|
|
|||
|
|
|
n |
|
|
|
|
f (a, b) F[axi b yi], |
n 4. |
||||||
|
|
|
i 1 |
|
|
|
|
Для составления системы (3) для определения коэффициентов a и b предварительно вычисляем
n |
n |
n |
n |
Fxi yi 21, |
Fxi2 39, |
Fxi 11, |
Fyi 10. |
i 1 |
i 1 |
i 1 |
i 1 |
Система (3) принимает вид
21 39a 11b 0,
10 11a 4b 0.

228 Глава 4. Дифференциальное исчисление функций многих переменных
Решая эту систему, находим a 26 , b 159 . Искомая прямая есть 35 35
Y 26 x 159 .
3535
4.8.Векторная функция скалярного аргумента
Задачи, приводящие к понятию векторной функции скалярного аргумен та. Предел и производная векторной функции. Механический смысл пер вой и второй производных векторной функции скалярного аргумента.
4.8.1. Задачи, приводящие к понятию векторной функции скалярного аргумента
Исаак Ньютон в своих трудах неоднократно указывал на тесную связь между механикой и математикой. Он подчеркивал, что многие основные понятия математикиM62родились из практической механики, имеющей в своей основе непосредственную практическую деятель ность людей.
За три столетия, отделяющие нас от эпохи Ньютона, сохранилась главная задача физико математических наук — объяснение и точное описание явлений природы.
До сих пор мы занимались изучением тех процессов и явлений, которые описываются скалярной функцией одного или нескольких скалярных аргументов, т. е. функциональной зависимостью вида
y f (x) или y f (x1, x2, , xn).
Аналогично можно дать понятие век торной функции скалярного аргумента. Обратимся к простейшей механической модели, которая приведет нас к такому по нятию. Пусть материальная точка М пере мещается в пространстве. Рассмотрим в пространстве декартову прямоугольную систему координат OXYZ и обозначим че рез x, y, z координаты точки М. Рассмот рим вектор OM r, начало которого сов
Рис. 4.8 |
падает с началом координат, а конец с |
|

4.8. Векторная функция скалярного аргумента |
229 |
точкой M(x, y, z). Такой вектор назовем радиус вектором. Выразим этот вектор через его проекции на оси координат
r xi yj zk. (1) Пусть закон движения точки М задан, т. е. пусть координаты точ
ки x, y, z являются функциями времени t:
x ((t), y >(t), z K(t). |
(2) |
||||||||
Тогда формулу (1) можно переписать так: |
|
||||||||
|
|
|
|
|
|
|
|
(1 ) |
|
|
|
((t)i >(t)j K(t)k |
|||||||
r |
|||||||||
или коротко |
(1 ) |
||||||||
|
|
|
|
|
|
|
|||
|
|
r |
r(t). |
||||||
Говорят, что формулы (1 ) и (1 ) определяют векторную функцию скалярного аргумента t.
При изменении параметра t вектор r(t) меняется по величине и на правлению, а точка М, конецM62вектора r, опишет в пространстве некото рую линию, которую называют годографом вектора r r(t). Уравнения (1 ) и (1 ) называют векторным уравнением линии в пространстве. Уравнение (2) называют параметрическим уравнением линии в про странстве.
Уравнение (1 ) можно рассматривать как математическую модель движения материальной точки.
Как показывает практика, уравнением вида (1 ) могут быть описа ны многие физические процессы. Поэтому мы займемся более под робным изучением свойств векторной функции скалярного аргумента, отвлекшись от конкретного содержания задач.
4.8.2. Предел и производная векторной функции скалярного аргумента
Допустим, что
lim ((t) (0,
t t0
lim >(t) >0,
t t0
lim K(t) K0.
t t0

230 |
|
Глава 4. Дифференциальное исчисление функций многих переменных |
|
|||||||
Тогда говорят, что вектор r0 (0i >0 j K0 k |
есть предел вектора r(t) |
|||||||||
при t t0 и пишут: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
lim r(t) r0. |
|
|
|
|
|
|
|
|
|
|
t t0 |
|
|
|
|
Из последнего соотношения вытекают очевидные равенства |
|
|||||||||
|
|
lim | r(t) r0| lim |
(((t) (0)2 (>(t) >0)2 (K(t) K0)2 |
0; |
|
|||||
|
|
t t0 |
|
t t0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim | r(t) | r0 |. |
|
|
|
|
|
|
|
|
|
|
t t0 |
|
|
|
|
|
|
|
|
|
|
Перейдем теперь к вопросу о произ |
||||
|
|
|
|
|
|
водной векторной функции. Пусть век |
||||
|
|
|
|
|
|
торная функция (1 ) является радиус век |
||||
|
|
|
|
|
|
тором точки M(x, y, z), т. е. r(t) OM. При |
||||
|
|
|
|
|
|
изменении параметра t точка М описыва |
||||
|
|
|
|
|
|
ет годограф С. Будем считать, что функ |
||||
|
|
|
|
|
|
ции (, >, K дифференцируемы по t. Выбе |
||||
|
|
Рис. 4.9 |
|
|
рем и зафиксируем значение параметра t. |
|||||
|
|
|
|
Ему соответствует точка М и вектор |
r(t). |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
M62 |
|
|
|||
Рассмотрим другое значение параметра t -t. Ему соответствует точка |
||||||||||
M1 |
и |
вектор |
r(t -t). |
Рассмотрим |
вектор |
-r MM1. |
Очевидно, |
|||
-r r(t -t) r(t) — приращение вектор функции r(t) в точке t. Рас |
||||||||||
смотрим отношение |
-r . Это вектор, коллинеарный вектору -r, так |
|||||||||
|
|
|
|
-t |
|
|
1 . |
|
|
|
как отличается от него множителем |
|
|
|
|||||||
|
|
|
|
|
|
|
-t |
|
|
|
|
Производной вектор функции r(t) в точке t по скалярному аргу |
|||||||||
менту t называется новый вектор, равный пределу отношения прира |
||||||||||
щения вектор функции -r к приращению аргумента -t при условии, |
||||||||||
что -t 0. Таким образом, по определению, |
|
|
|
|||||||
|
|
|
|
|
dr |
r (t) lim -r . |
|
|
(3) |
|
|
|
|
|
|
dt |
-t 0 -t |
|
|
|
|
Выразим производную вектор функции через ее проекции на оси ко |
||||||||||
ординат. |
|
|
|
|
|
|
|
|
||
