Основы высшей математики для инженеров 2009

3.5. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка. Методы интегриро вания некоторых специальных классов тригонометрических функций.

3.5.1. Универсальная тригонометрическая подстановка

Рассмотрим интеграл вида

DR(sin x, cos x) dx,

где R — рациональная функция sin x и cos x. Покажем, что с помощью

подстановки tg x t этот интеграл всегда приводится к интегралу от 2

рациональной функции. Имеем

162Глава 3. Интегральное исчисление функций одной переменной

Пр и м е р 2.

Итак, с помощью указанной подстановки можно проинтегриро вать любую функцию вида R(sin x, cos x). Поэтому подстановка назы вается универсальной. Однако ее применение иногда приводит к слишком сложным рациональным функциям. Поэтому полезно знать и другие методы интегрирования тригонометрических функций.

3.5.2. Методы интегрирования некоторых специальных классов тригонометрических функций

5. Dsinm x cosn x dx J,

где m или n — нечетное. Пусть m 2k 1.

J Dsin2k 1x cosn x dx D(1 cos2 x)k cosn x d(cos x) D(1 t2)ktndt,

в степени k и p, получим cos2 x в четных и нечетных степенях. Нечет ные степени интегрируются, как было указано выше, а с четными сте пенями вновь проделываем ту же процедуру. Таким образом, дойдем до интегралов вида Dcos kx dx, которые легко вычисляются.

dx

7. D sinm x cosn x , где m и n — целые числа одинаковой четности.

J D(cosec x)m(sec x)n 2 d(tg x) tg x t.

11

2 M62(tg x 1)2 d(tg x) Dt2 t 1 dt

tg x

8.Dsin mx cos nx dx, Dsin mx sin nx dx, Dcosmx cos nx dx вычисляются

сиспользованием следующих формул:

sin mx cos nx 1 [sin (m n) x sin (m n) x], 2

cosmx cos nx 1 [cos(m n) x cos(m n) x], 2

sin mx sin nx 1 [cos(m n) x cos(m n) x]. 2

3.6. Тригонометрические подстановки

Тригонометрические подстановки. О функциях, интегралы от которых не выражаются через элементарные функции.

3.6.1. Тригонометрические подстановки

Рассмотрим интеграл вида

J DR(x, 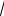ax2 bx c) dx,

где a 0, b2 4 ac 0. Покажем, что этот интеграл может быть преобра зован к интегралу вида

DR(cost, sin t) dx.

В квадратном трехчлене ax2 bx c выделим полный квадрат:

166Глава 3. Интегральное исчисление функций одной переменной

4.a 0, c b2 0.

4a

Вэтом случае 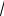ax2 bx c есть комплексное число при любом x. Таким образом, наш интеграл преобразуется к интегралу одного из

следующих типов.

I. DR(z, m2 z2 n2 ) dz.

II. DR(z, m2 z2 n2 ) dz.

III. DR(z, n2 m2 z2 ) dz.

Для вычисления каждого из этих интегралов используется триго нометрическая подстановка, позволяющая свести его к интегралу от рациональной функции от sin t и cost.

I. DR(z, 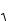n2 m2 z2 ) dz. M62n

Здесь используется подстановка z sin t. m